More Powerful LR Parsers

More Powerful LR Parsers

1 Canonical LR(1) Items

2 Constructing LR(1) Sets of Items

3 Canonical LR(1) Parsing Tables

4 Constructing LALR Parsing Tables

5 Efficient Construction of LALR Parsing Tables

6 Compaction of LR Parsing Tables

7 Exercises for Section 4.7

In this section, we shall extend the previous LR parsing techniques to use one symbol of lookahead on the input. There are two different methods:

            The "canonical-LR" or just "LR" method, which makes full use of the lookahead symbol(s). This method uses a large set of items, called the LR(1) items.

            The "lookahead-LR" or "LALR" method, which is based on the LR(0) sets of items, and has many fewer states than typical parsers based on the LR(1) items. By carefully introducing lookaheads into the LR(0) items, we can handle many more grammars with the LALR method than with the SLR method, and build parsing tables that are no bigger than the SLR tables. LALR is the method of choice in most situations.

After introducing both these methods, we conclude with a discussion of how to compact LR parsing tables for environments with limited memory.

1. Canonical LR(1) Items

We shall now present the most general technique for constructing an LR parsing table from a grammar. Recall that in the SLR method, state i calls for reduction by A -» a if the set of items I* contains item [A -> a] and a is in FOLLOW(A). In some situations, however, when state i appears on top of the stack, the viable prefix ba on the stack is such that bA cannot be followed by a in any right-sentential form. Thus, the reduction by A -> a should be invalid on input a.

Example 4 . 5 1 : Let us reconsider Example 4.48, where in state 2 we had item R --> L , which could correspond to A —> a above, and a could be the = sign, which is in FOLLOW(E).          Thus, the SLR parser calls for reduction by R- - > L in state 2 with = as the next input (the shift action is also called for, because  of item S -» L=R in state 2). However, there is no right-sentential form of the grammar in Example 4.48 that begins R =  •••        .         Thus state 2,  which is the state corresponding to viable prefix L only, should not really call for reduction of that L to R.

It is possible to carry more information in the state that will allow us to rule out some of these invalid reductions by A —»• a. By splitting states when necessary, we can arrange to have each state of an LR parser indicate exactly which input symbols can follow a handle a for which there is a possible reduction to  A.

The extra information is incorporated into the state by redefining items to include a terminal symbol as a second component. The general form of an item becomes [A ->• a • b,a], where A -- > ab is a production and a is a terminal or the right endmarker $. We call such an object an LR(1) item. The 1 refers to the length of the second component, called the lookahead of the item.6 The lookahead has no effect in an item of the form [A  a-(3, a], where ft is not e, but an item of the form [A ->• a, a] calls for a reduction by A -» a only if the next input symbol is a. Thus, we are compelled to reduce by A -» a only on those input symbols a for which [A -» a, a] is an LR(1) item in the state on top of the stack. The set of such a's will always be a subset of FOLLOW(A), but it could be a proper subset, as in Example 4.51.

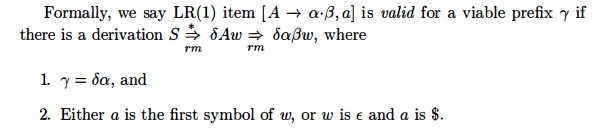
Example 4 . 5 2 :  Let us consider the grammar

2. Constructing LR(1) Sets of Items

The method for building the collection of sets of valid LR(1) items is essentially the same as the one for building the canonical collection of sets of LR(0) items. We need only to modify the two procedures CLOSURE and GOTO.

Algorithm 4 . 5 3 :  Construction of the sets of LR(1) items.

INPUT :  An augmented grammar G'.

OUTPUT : The sets of LR(1) items that are the set of items valid for one or more viable prefixes of G'.

METHOD :  The          procedures CLOSURE          and  GOTO         and the  main  routine  items for constructing the sets of items were shown in Fig. 4.40.

Example 4.54 :   Consider the following augmented grammar.

Note that I(6) differs from      I(3) only in second components. We shall see that it is common for several sets of LR(1) items for a grammar to have the same first components and differ in their second components. When we construct the collection of sets of LR(0) items for the same grammar, each set of LR(0) items will coincide with the set of first components of one or more sets of LR(1) items. We shall have more to say about this phenomenon when we discuss LALR parsing.

Continuing with the GOTO function for I2 , GOTO ( I 2 , d) is seen to be

The remaining sets of items yield no GOTO's, so we are done. Figure 4.41 shows the ten sets of items with their goto's.

3. Canonical LR(1) Parsing Tables

We now give the rules for constructing the LR(1) ACTION and GOTO functions from the sets of LR(1) items. These functions are represented by a table, as before. The only difference is in the values of the entries.

Algorithm 4.56 : Construction of canonical-LR parsing tables.

INPUT :  An augmented grammar G'.

OUTPUT : The canonical-LR parsing table functions ACTION and GOTO for G'.

METHOD :

The table formed from the parsing action and goto functions produced by Algorithm 4.44 is called the canonical LR(1) parsing table. An LR parser using this table is called a canonical-LR(l) parser. If the parsing action function has no multiply defined entries, then the given grammar is called an LR(1) grammar. As before, we omit the "(1)" if it is understood-

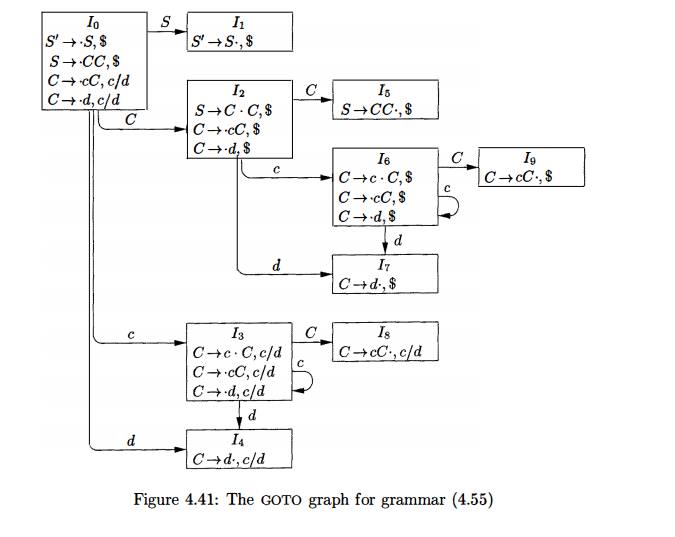
Example 4.57 :  The canonical parsing table for      grammar (4.55) is shown in Pig.  4.42. Productions  1,  2,       and  3  are  5   -->  CC,  C  ->  cC,  and     C  -> d, respectively.

Every SLR(l) grammar is an LR(1) grammar, but for an SLR(l) grammar the canonical LR parser may have more states than the SLR parser for the same grammar. The grammar of the previous examples is SLR and has an SLR parser with seven states, compared with the ten of Fig. 4.42.

4. Constructing LALR Parsing Tables

We now introduce our last parser construction method, the L A L R (lookahead-L R ) technique.  This method is often used in practice, because the tables obtained by it are considerably smaller than the canonical LR tables, yet most common syntactic tained by it are considerably smaller than the canonical LR tables, yet most common syntactic constructs of programming languages can be expressed con-veniently by an L A L R grammar. The same is almost true for S L R grammars, but there are a few constructs that cannot be conveniently handled by S L R techniques (see Example 4.48, for example).

For a comparison of parser size, the S L R and L A L R tables for a grammar always have the same number of states, and this number is typically several hundred states for a language like C. The canonical LR table would typically have several thousand states for the same-size language. Thus, it is much easier and more economical to construct S L R and L A L R tables than the canonical L R tables.

By way of introduction, let us again consider grammar (4.55), whose sets of L R ( 1 ) items were shown in Fig. 4.41. Take a pair of similar looking states, such as I4 and I 7 . Each of these states has only items with first component C -> d-. In I 4 , the lookaheads are c or d; in I 7 , $ is the only lookahead.

To see the difference between the roles of I4 and I7 in the parser, note that the grammar generates the regular language c*dc*d. When reading an input cc • • • cdcc • • cd, the parser shifts the first group of c's and their following d onto the stack, entering state 4 after reading the d. The parser then calls for a reduction by C -» d, provided the next input symbol is c or d. The requirement that c or d follow makes sense, since these are the symbols that could begin strings in c*d. If $ follows the first d, we have an input like ccd, which is not in the language, and state 4 correctly declares an error if $ is the next input.

The parser enters state 7 after reading the second d.  Then, the parser must see $ on the input, or it started with a string not of the form c*dc*d. It thus makes sense that state 7 should reduce by C -» d on input $ and declare error on inputs c or d.

Let us now replace I4 and I7 by I47, the union of I4 and I7, consisting of the set of three items represented by [C ->• d-, c/d/$]. The goto's on d to I4 or I7 from I 0 , I2, I3, and I6 now enter I47 . The action of state 47 is to reduce on any input. The revised parser behaves essentially like the original, although it might reduce d to C in circumstances where the original would declare error, for example, on input like ccd or cdcdc. The error will eventually be caught; in fact, it will be caught before any more input symbols are shifted.

More generally, we can look for sets of LR(1) items having the same core, that is, set of first components, and we may merge these sets with common cores into one set of items. For example, in Fig. 4.41, I4 and Ij form such a pair, with 

Since the core of GOTO(I,X) depends only on the core of /, the goto's of merged sets can themselves be merged. Thus, there is no problem revising the goto function as we merge sets of items. The action functions are modified to reflect the non-error actions of all sets of items in the merger.

Suppose we have an LR(1) grammar, that is, one whose sets of LR(1) items produce no parsing-action conflicts. If we replace all states having the same core with their union, it is possible that the resulting union will have a conflict, but it is unlikely for the following reason: Suppose in the union there is a conflict on lookahead a because there is an item [A ->• a-, a] calling for a reduction by A -» a, and there is another item [B -» abg, b] calling for a shift.  Then some set of items from which the union was formed has item [A -» a-, a], and since the cores of all these states are the same, it must have an item [B -> abg,c] for some c. But then this state has the same shift/reduce conflict on a, and the grammar was not LR(1) as we assumed. Thus, the merging of states with common cores can never produce a shift/reduce conflict that was not present in one of the original states, because shift actions depend only on the core, not the lookahead.

It is possible, however, that a merger will produce a reduce/reduce conflict, as the following example shows.

Example 4.58 : Consider the grammar

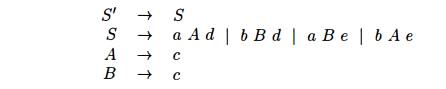
which generates the four strings acd, ace, bed, and bee. The reader can check that the grammar is LR(1) by constructing the sets of items. Upon doing so, 

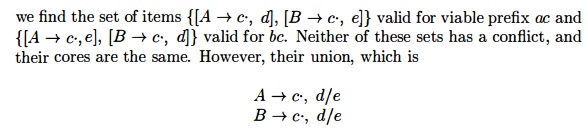
generates a reduce/reduce conflict, since reductions by both A -> c and B -> c are called for on inputs d and e. •

We are now prepared to give the first of two LALR table-construction al-gorithms. The general idea is to construct the sets of LR(1) items, and if no conflicts arise, merge sets with common cores. We then construct the parsing table from the collection of merged sets of items. The method we are about to describe serves primarily as a definition of LALR(l) grammars. Constructing the entire collection of LR(1) sets of items requires too much space and time to be useful in practice.

Algorithm 4 .5 9 : An easy, but space-consuming LALR table construction.

INPUT :  An augmented grammar G'.

OUTPUT : The LALR parsing-table functions ACTION and GOTO for G'.

METHOD :

 The table produced by Algorithm 4.59 is called the LALR parsing table for G. If there are no parsing action conflicts, then the given grammar is said to be an LALR(l) grammar. The  collection  of sets of items  constructed in  step (3) is called the  LALR(l) collection.  

Example 4.60 :  Again consider grammar (4.55) whose GOTO graph was shown in Fig. 4.41. As we mentioned, there are three pairs of sets of items that can be merged.  I3 and I6 are replaced by their union:

Figure 4.43:  LALR parsing table for the grammar of Example 4.54

To see how the GOTO's are computed, consider GOTO(I3 6 , C). In the original set of LR(1) items, GOTO(I3, C) = h, and Is is now part of I89, so we make GOTO(I36,C) be 789- We could have arrived at the same conclusion if we considered I6, the other part of I3 g. That is, GOTO(I6, C) = Ig, and IQ is now part of Ig9. For another example, consider GOTO(I2,c), an entry that is exercised after the shift action of I2 on input c. In the original sets of LR(1) items, GOTO(I2,c) = I6. Since I6 is now part of 736, GOTO(I2,c) becomes I36. Thus, the entry in Fig. 4.43 for state 2 and input c is made s36, meaning shift and push state 36 onto the stack. •

When presented with a string from the language c*dc*d, both the LR parser of Fig. 4.42 and the LALR parser of Fig. 4.43 make exactly the same sequence of shifts and reductions, although the names of the states on the stack may differ. For instance, if the LR parser puts I3 or I6 on the stack, the LALR parser will put I36 on the stack. This relationship holds in general for an LALR grammar. The LR and LALR parsers will mimic one another on correct inputs.

When presented with erroneous input, the LALR parser may proceed to do some reductions after the LR parser has declared an error. However, the LALR parser will never shift another symbol after the LR parser declares an error. For example, on input ccd followed by $, the LR parser of Fig. 4.42 will put

0 3 3 4

on the stack, and in state 4 will discover an error, because $ is the next input symbol and state 4 has action error on $. In contrast, the LALR parser of Fig. 4.43 will make the corresponding moves, putting

0 36 36 47

on the stack. But state 47 on input $ has action reduce C —>• d. The LALR parser will thus change its stack to

0 36 36 89

Now the action of state 89 on input $ is reduce C -»• cC.  The stack becomes

0 36 89

whereupon a similar reduction is called for, obtaining stack

0 2

Finally, state 2 has action error on input $, so the error is now discovered.

5. Efficient Construction of LALR Parsing Tables

There are several modifications we can make to Algorithm 4.59 to avoid con-structing the full collection of sets of LR(1) items in the process of creating an LALR(l) parsing table.

•  First, we can represent any set of LR(0) or LR(1) items I by its kernel, that is, by those items that are either the initial item — [S' -S] or [S' ->• -S, $] — or that have the dot somewhere other than at the beginning of the production body.

            We can construct the LALR(l)-item kernels from the LR(0)-item kernels by a process of propagation and spontaneous generation of lookaheads, that we shall describe shortly.

            If we have the LALR(l) kernels, we can generate the LALR(l) parsing table by closing each kernel, using the function CLOSURE of Fig. 4.40, and then computing table entries by Algorithm 4.56, as if the LALR(l) sets of items were canonical LR(1) sets of items.

Example 4.61 : We shall use as an example of the efficient LALR(l) table-construction method the non-SLR grammar from Example 4.48, which we re-produce below in its augmented form:

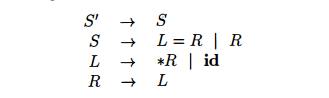
The complete sets of LR(0) items for this grammar were shown in Fig. 4.39. The kernels of these items are shown in Fig. 4.44.

Figure 4.44:  Kernels of the sets of LR(0) items for grammar (4.49)

Algorithm 4.62 : Determining lookaheads.

INPUT : The kernel K of a set of LR(0) items / and a grammar symbol X.

OUTPUT : The lookaheads spontaneously generated by items in I for kernel

items in GOTO ( I , X ) and the items in i" from which lookaheads are propagated to kernel items in GOTO ( / , X ).

METHOD : The algorithm is given in Fig. 4.45.

Figure 4.45:  Discovering propagated and spontaneous lookaheads

We are now ready to attach lookaheads to the kernels of the sets of LR(0) items to form the sets of LALR(l) items. First, we know that $ is a looka-head for S' -y -S in the initial set of LR(0) items. Algorithm 4.62 gives us all the lookaheads generated spontaneously. After listing all those lookaheads, we must allow them to propagate until no further propagation is possible. There are many different approaches, all of which in some sense keep track of "new" lookaheads that have propagated into an item but which have not yet propa-gated out. The next algorithm describes one technique to propagate lookaheads to all items.

Algorithm 4.63 : Efficient computation of the kernels of the LALR(l) collec-tion of sets of items.

INPUT :  An augmented grammar G'.

OUTPUT : The kernels of the LALR(l) collection of sets of items for G'.

METHOD :

Construct the kernels of the sets of LR(0) items for G. If space is not at a premium, the simplest way is to construct the LR(0) sets of items, as in Section 4.6.2, and then remove the nonkernel items. If space is severely constrained, we may wish instead to store only the kernel items for each set, and compute GOTO for a set of items I by first computing the closure of/.

            Apply Algorithm 4.62 to the kernel of each set of LR(0) items and gram-mar symbol X to determine which lookaheads are spontaneously gener-ated for kernel items in GOTO(I, X), and from which items in I lookaheads

are propagated to kernel items in G O T O ( I , X ) .

            Initialize a table that gives, for each kernel item in each set of items, the associated lookaheads. Initially, each item has associated with it only those lookaheads that we determined in step (2) were generated sponta-neously.

            Make repeated passes over the kernel items in all sets. When we visit an item i, we look up the kernel items to which i propagates its lookaheads,

using information tabulated in step (2). The current set of lookaheads for i is added to those already associated with each of the items to which i propagates its lookaheads. We continue making passes over the kernel items until no more new lookaheads are propagated.

Example 4.6 4 : Let us construct the kernels of the LALR(l) items for the grammar of Example 4.61. The kernels of the LR(0) items were shown in Fig. 4.44. When we apply Algorithm 4.62 to the kernel of set of items Io, we first compute CLOSURE({[S" ->> S, #]}), which is

In Fig. 4.47, we show steps (3) and (4) of Algorithm 4.63. The column labeled INIT shows the spontaneously generated lookaheads for each kernel item. These are only the two occurrences of = discussed earlier, and the spontaneous lookahead $ for the initial item S' - 5 .

On the first pass, the lookahead $ propagates from S' —>• S in Io to the six items listed in Fig. 4.46.    The lookahead = propagates from L -> *-R in i4 to items L -» * R- in I7  and     R -> L- in I8-  It also propagates to       itself and to L —»• id • in I5, but these lookaheads are already present. In the second and third passes, the only new lookahead propagated is $, discovered for the successors of i2 and i4 on pass 2 and for the successor of IQ on pass 3. No new lookaheads are propagated on pass 4, so the final set of lookaheads is shown in the rightmost column of Fig. 4.47.

Note that the shift/reduce conflict found in Example 4.48 using the SLR method has disappeared with the LALR technique. The reason is that only lookahead $ is associated with R -» L- in I2 , so there is no conflict with the parsing action of shift on = generated by item S -» L=R in i 2 .

6. Compaction of LR Parsing Tables

A typical programming language grammar with 50 to 1 0 0 terminals and 1 0 0 productions may have an L A L R parsing table with several hundred states. The action function may easily have 2 0 , 0 0 0 entries, each requiring at least 8 bits to encode. On small devices, a more efficient encoding than a two-dimensional array may be important. We shall mention briefly a few techniques that have been used to compress the and fields of an L R parsing table.

One useful technique for compacting the action field is to recognize that usually many rows of the action table are identical. For example, in Fig. 4 . 4 2 , states 0 and 3 have identical action entries, and so do 2 and 6. We can therefore save considerable space, at little cost in time, if we create a pointer for each state into a one-dimensional array. Pointers for states with the same actions point to the same location. To access information from this array, we assign each terminal a number from zero to one less than the number of terminals, and we use this integer as an offset from the pointer value for each state. In a given state, the parsing action for the ith terminal will be found i locations past the pointer value for that state.

Further space efficiency can be achieved at the expense of a somewhat slower parser by creating a list for the actions of each state. The list consists of (terminal-symbol, action) pairs. The most frequent action for a state can be  placed at the end of the list, and in place of a terminal we may use the notation "any," meaning that if the current input symbol has not been found so far on the list, we should do that action no matter what the input is. Moreover, error entries can safely be replaced by reduce actions, for further uniformity along a row. The errors will be detected later, before a shift move.

Example 4.6 5 : Consider the parsing table of Fig. 4.37. First, note that the actions for states 0, 4, 6, and 7 agree. We can represent them all by the list

In state 2, we can replace the error entries by r2, so reduction by production 2 will occur on any input but *. Thus the list for state 2 is

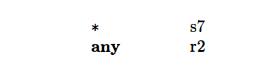
State 3 has only error and r4 entries. We can replace the former by the latter, so the list for state 3 consists of only the pair (any, r4). States 5, 10, and 11 can be treated similarly. The list for state 8 is

We can also encode the G O T O table by a list, but here it appears more efficient to make a list of pairs for each nonterminal A. Each pair on the list for A is of the form (currentState,nextState), indicating

 GOTO [currentState, A] = next State

This technique is useful because there tend to be rather few states in any one column of the GOTO table. The reason is that the GOTO on nonterminal A can only be a state derivable from a set of items in which some items have A immediately to the left of a dot. No set has items with X and Y immediately to the left of a dot if X ^ Y. Thus, each state appears in at most one GOTO column.

For more space reduction, we note that the error entries in the goto table are never consulted. We can therefore replace each error entry by the most common non-error entry in its column. This entry becomes the default; it is represented

in the list for each column by one pair with any in place of currentState.

E x a m p l e 4 . 6 6 :  Consider Fig. 4.37 again.  The column for F has entry 10 for state 7, and all other entries are either 3 or error. We may replace error by 3 and create for column F the list

For column E we may choose either 1 or 8 to be the default; two entries are necessary in either case. For example, we might create for column E the list

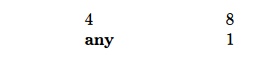
This space savings in these small examples may be misleading, because the total number of entries in the lists created in this example and the previous one together with the pointers from states to action lists and from nonterminals to next-state lists, result in unimpressive space savings over the matrix imple-mentation of Fig. 4.37. For practical grammars, the space needed for the list representation is typically less than ten percent of that needed for the matrix representation. The table-compression methods for finite automata that were discussed in Section 3.9.8 can also be used to represent LR parsing tables.

7. Exercises for Section 4.7

Exercise 4 . 7 . 1 :  Construct the

            canonical LR, and

LALR

sets of items for the grammar S-+SS + 1SS*1aof Exercise 4.2.1.

Exercise 4 . 7 . 2 : Repeat Exercise 4.7.1 for each of the (augmented) grammars of Exercise 4.2.2(a)-(g).

! Exercise 4 . 7 . 3 : For the grammar of Exercise 4.7.1, use Algorithm 4.63 to compute the collection of LALR sets of items from the kernels of the LR(0) sets of items.

! Exercise 4 . 7 . 4 : Show that the following grammar

is LR(1) but not LALR(l) .