Parser Generators

Parser Generators

1 The Parser Generator Yacc

2 Using Yacc with Ambiguous Grammars

3 Creating Yacc Lexical Analyzers with Lex

4 Error Recovery in Yacc

5 Exercises for Section 4.9

This section shows how a parser generator can be used to facilitate the construc-tion of the front end of a compiler. We shall use the LALR parser generator Yacc as the basis of our discussion, since it implements many of the concepts discussed in the previous two sections and it is widely available. Yacc stands for "yet another compiler-compiler," reflecting the popularity of parser generators in the early 1970s when the first version of Yacc was created by S. C. Johnson. Yacc is available as a command on the UNIX system, and has been used to help implement many production compilers.

1. The Parser Generator Yacc

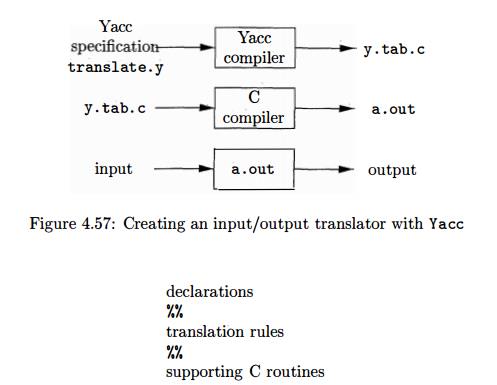
A translator can be constructed using Yacc in the manner illustrated in Fig. 4.57. First, a file, say translate.y, containing a Yacc specification of the translator is prepared. The UNIX system command

yacc  translate.y

transforms the file translate.y into a C program called y.tab.c using the LALR method outlined in Algorithm 4.63. The program y.tab.c is a repre-sentation of an LALR parser written in C, along with other C routines that the user may have prepared. The LALR parsing table is compacted as described in Section 4.7. By compiling y.tab.c along with the ly library that contains the LR parsing program using the command

cc  y.tab.c  -ly

we obtain the desired object program a. out that performs the translation spec-ified by the original Yacc program . ⁷ If other procedures are needed, they can be compiled or loaded with y.tab.c, just as with any C program.

A Yacc source program has three parts:

Example 4.69 : T0 illustrate how to prepare a Yacc source program, let us construct a simple desk calculator that reads an arithmetic expression, evaluates it, and then prints its numeric value. We shall build the desk calculator starting with the with the following grammar for arithmetic expressions:

E       ->      E       +       T       |         T

T         -->        T       *        F       |         F

F       -->     ( E ) |        digit

The token digit is a single digit between 0 and 9. A Yacc desk calculator program derived from this grammar is shown in Fig. 4.58. •

The  Declarations  Part

There are two sections in the declarations part of a Yacc program; both are optional. In the first section, we put ordinary C declarations, delimited by .'/.{ and '/,}. Here we place declarations of any temporaries used by the translation rules or procedures of the second and third sections. In Fig. 4.58, this section contains only the include-statement

# i n c l u d e         <ctype. h>

that causes the C preprocessor to include the standard header file <ctype. h> that contains the predicate i s d i g i t .

Also in the declarations part are declarations of grammar tokens. In Fig. 4.58, the statement

%token DIGIT

declares DIGIT to be  a token.   Tokens declared in this  section can then  be used in the second and third parts of the Yacc specification.  If Lex is used to create the lexical analyzer that passes token to the Yacc parser, then these token declarations are also made available to the analyzer generated by Lex, as discussed in Section 3.5.2.

The  Translation Rules  Part

In the part of the Yacc specification after the first %% pair, we put the translation rules. Each rule consists of a grammar production and the associated semantic action. A set of productions that we have been writing:

In a Yacc production, unquoted strings of letters and digits not declared to be tokens are taken to be nonterminals. A quoted single character, e.g. ' c', is taken to be the terminal symbol c, as well as the integer code for the token represented by that character (i.e., Lex would return the character code for ' c' to the parser, as an integer). Alternative bodies can be separated by a vertical bar, and a semicolon follows each head with its alternatives and their semantic actions. The first head is taken to be the start symbol.

A Yacc semantic action is a sequence of C statements. In a semantic action, the symbol $$ refers to the attribute value associated with the nonterminal of the head, while $i refers to the value associated with the ith grammar symbol (terminal or nonterminal) of the body. The semantic action is performed when-ever we reduce by the associated production, so normally the semantic action computes a value for $$ in terms of the $i's. In the Yacc specification, we have

Written the two    E-productions

Note that the nonterminal term in the first production is the third grammar symbol of the body, while + is the second. The semantic action associated with the first production adds the value of the expr and the term of the body and assigns the result as the value for the nonterminal expr of the head. We have omitted the semantic action for the second production altogether, since copying the value is the default action for productions with a single grammar symbol in the body. In general, { $$ = $ 1 ;  } is the default semantic action.

Notice that we have added a new starting production

to the Yacc specification. This production says that an input to the desk calculator is to be an expression followed by a newline character. The semantic action associated with this production prints the decimal value of the expression followed by a newline character.

The Supporting C - Routines Part

The third part of a Yacc specification consists of supporting C-routines. A lexical analyzer by the name y y l e x O must be provided. Using Lex to produce y y l e x O is a common choice; see Section 4.9.3. Other procedures such as error recovery routines may be added as necessary.

The lexical analyzer y y l e x O produces tokens consisting of a token name and its associated attribute value. If a token name such as DIGIT is returned, the token name must be declared in the first section of the Yacc specification. The attribute value associated with a token is communicated to the parser through a Yacc-defined variable y y l v a l .

The lexical analyzer in Fig. 4.58 is very crude. It reads input characters one at a time using the C-function get char ( ) . If the character is a digit, the value of the digit is stored in the variable y y l v a l , and the token name DIGIT is returned. Otherwise, the character itself is returned as the token name.

2. Using Yacc with Ambiguous Grammars

Let us now modify the Yacc specification so that the resulting desk calculator becomes more useful. First, we shall allow the desk calculator to evaluate a sequence of expressions, one to a line. We shall also allow blank lines between expressions. We do so by changing the first rule to

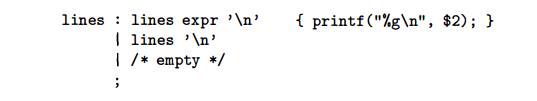
In Yacc, an empty alternative, as the third line is, denotes e.

Second, we shall enlarge the class of expressions to include numbers instead of single digits and to include the arithmetic operators +, —, (both binary and unary), *, and /. The easiest way to specify this class of expressions is to use

the ambiguous grammar

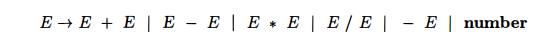
The resulting Yacc specification is shown in Fig. 4.59.

Since the grammar in the Yacc specification in Fig. 4.59 is ambiguous, the LALR algorithm will generate parsing-action conflicts. Yacc reports the num-ber of parsing-action conflicts that are generated. A description of the sets of items and the parsing-action conflicts can be obtained by invoking Yacc with a -v option. This option generates an additional file y . o u t p u t that contains the kernels of the sets of items found for the grammar, a description of the parsing action conflicts generated by the LALR algorithm, and a readable represen-tation of the LR parsing table showing how the parsing action conflicts were resolved. Whenever Yacc reports that it has found parsing-action conflicts, it is wise to create and consult the file y. output to see why the parsing-action conflicts were generated and to see whether they were resolved correctly. Unless otherwise instructed Yacc will resolve all parsing action conflicts using the following two rules:

     A reduce/reduce conflict is resolved by choosing the conflicting production listed first in the Yacc specification.

     A shift/reduce conflict is resolved in favor of shift. This rule resolves the shift /reduce conflict arising from the dangling-else ambiguity correctly.

Since these default rules may not always be what the compiler writer wants, Yacc provides a general mechanism for resolving shift/reduce conflicts. In the declarations portion, we can assign precedences and associativities to terminals. The declaration

'/.left ' + ' '-'

makes + and - be of the same precedence and be left associative. We can declare an operator to be right associative by writing

'/.right

and we can force an operator to be a nonassociative binary operator (i.e., two occurrences of the operator cannot be combined at all) by writing

°/₀ nonassoc                                ' < '

The tokens are given precedences in the order in which they appear in the declarations part, lowest first. Tokens in the same declaration have the same precedence. Thus, the declaration

'/.right UMINUS

in Fig. 4.59 gives the token UMINUS a precedence level higher than that of the five preceding terminals.

Yacc resolves shift/reduce conflicts by attaching a precedence and associa-tivity to each production involved in a conflict, as well as to each terminal involved in a conflict. If it must choose between shifting input symbol a and re-ducing by production A ->• a, Yacc reduces if the precedence of the production is greater than that of a, or if the precedences are the same and the associativity of the production is left. Otherwise, shift is the chosen action.

Normally, the precedence of a production is taken to be the same as that of its rightmost terminal. This is the sensible decision in most cases. For example, given productions

E       ->•     E + E |         E+E

we  would  prefer to  reduce  by E -^-E+E with  lookahead  +, because the  +  in the body has the same precedence as the lookahead, but is left associative. With lookahead *, we would prefer to shift, because the lookahead has higher precedence than the + in the production.

In those situations where the rightmost terminal does not supply the proper precedence to a production, we can force a precedence by appending to a pro-duction the tag

°/.prec  (terminal)

The precedence and associativity of the production will then be the same as that of the terminal, which presumably is defined in the declaration section. Yacc does not report shift/reduce conflicts that are resolved using this precedence and associativity mechanism.

This "terminal" can be a placeholder, like UMINUS in Fig. 4.59; this termi-nal is not returned by the lexical analyzer, but is declared solely to define a precedence for a production. In Fig. 4.59, the declaration

•/.right UMINUS

assigns to the token UMINUS a precedence that is higher than that of * and /. In the translation rules part, the tag:

⁰ /,prec UMINUS

at the end of the production

expr                                    :  ' - '       expr

makes the unary-minus operator in this production have a higher precedence than any other operator.

3. Creating Yacc Lexical Analyzers with Lex

Lex was designed to produce lexical analyzers that could be used with Yacc. The Lex library 11 will provide a driver program named y y l e x O , the name required by Yacc for its lexical analyzer. If Lex is used to produce the lexical analyzer,

we replace the routine y y l e x O  in the third part of the Yacc specification by the  statement

# i n c l u d e                        "lex . yy . c"

and we have each Lex action return a terminal known to Yacc. By using the # i n c l u d e "lex . yy . c" statement, the program yylex has access to Yacc's names for tokens, since the Lex output file is compiled as part of the Yacc output file y.tab.c.

Under the UNIX system, if the Lex specification is in the file first . l and the Yacc specification in second . y, we can say         lex     first.1

          yacc   second.y

          cc  y.tab.c  -ly  -11

to obtain the desired translator.

The Lex specification in Fig. 4.60 can be used in place of the lexical analyzer in Fig. 4.59. The last pattern, meaning "any character," must be written 1n| . since the dot in Lex matches any character except newline,

Figure 4.60:  Lex specification for yylexQ in Fig. 4.59

4. Error Recovery in Yacc

In Yacc, error recovery uses a form of error productions. First, the user de-cides what "major" nonterminals will have error recovery associated with them. Typical choices are some subset of the nonterminals generating expressions, statements, blocks, and functions. The user then adds to the grammar error productions of the form A -» error a, where A is a major nonterminal and a is a string of grammar symbols, perhaps the empty string; error is a Yacc reserved word. Yacc will generate a parser from such a specification, treating the error productions as ordinary productions.

However, when the parser generated by Yacc encounters an error, it treats the states whose sets of items contain error productions in a special way. On encountering an error, Yacc pops symbols from its stack until it finds the top-most state on its stack whose underlying set of items includes an item of the form A —> • error a. The parser then "shifts" a fictitious token error onto the stack, as though it saw the token error on its input.

When cc is e, a reduction to A occurs immediately and the semantic action associated with the production A —>• • error (which might be a user-specified error-recovery routine) is invoked. The parser then discards input symbols until it finds an input symbol on which normal parsing can proceed.

If a is not empty, Yacc skips ahead on the input looking for a substring that can be reduced to a. If a consists entirely of terminals, then it looks for this string of terminals on the input, and "reduces" them by shifting them onto the stack. At this point, the parser will have error a on top of its stack. The parser will then reduce error a to A, and resume normal parsing.

For example, an error production of the form

would specify to the parser that it should skip just beyond the next semicolon on seeing an error, and assume that a statement had been found. The semantic routine for this error production would not need to manipulate the input, but could generate a diagnostic message and set a flag to inhibit generation of object code, for example.

E x a m p l e 4 . 7 0 : Figure 4.61 shows the Yacc desk calculator of Fig. 4.59 with the error production

lines  :  error  '\n'

This error production causes the desk calculator to suspend normal parsing when a syntax error is found on an input line. On encountering the error, the parser in the desk calculator starts popping symbols from its stack until it encounters a state that has a shift action on the token error. State 0 is such a state (in this example, it's the only such state), since its items include

lines  —y                                • error ' \ n '

Also, state 0 is always on the bottom of the stack. The parser shifts the token error onto the stack, and then proceeds to skip ahead in the input until it has found a newline character. At this point the parser shifts the newline onto the stack, reduces error ' 1 n ' to lines, and emits the diagnostic message "reenter previous line:". The special Yacc routine yyerrok resets the parser to its normal mode of operation. •

5. Exercises for Section 4.9

      Exercise 4 . 9 . 1 : Write a Yacc program that takes boolean expressions as input [as given by the grammar of Exercise 4.2.2(g)] and produces the truth value of the expressions.

      Exercise 4 . 9 . 2 : Write a Yacc program that takes lists (as defined by the grammar of Exercise 4.2.2(e), but with any single character as an element, not just a) and produces as output a linear representation of the same list; i.e., a

single list of the elements, in the same order that they appear in the input.

! Exercise 4 . 9 . 3 : Write a Yacc program that tells whether its input is a palin-drome (sequence of characters that read the same forward and backward).

! Exercise 4 . 9 . 4 : Write a Yacc program that takes regular expressions (as de-fined by the grammar of Exercise 4.2.2(d), but with any single character as an argument, not just a) and produces as output a transition table for a nonde-terministic finite automaton recognizing the same language.