Context-Free Grammars

Context-Free Grammars

1 The Formal Definition of a Context-Free Grammar

2 Notational Conventions

3 Derivations

4 Parse Trees and Derivations

5 Ambiguity

6 Verifying the Language Generated by a Grammar

7 Context-Free Grammars Versus Regular Expressions

8 Exercises for Section 4.2

Grammars were introduced in Section 2.2 to systematically describe the syntax of programming language constructs like expressions and statements. Using a syntactic variable stmt to denote statements and variable expr to denote expressions, the production

stmt  —>  if ( expr )  stmt else stmt     (4.4)

specifies the structure of this form of conditional statement. Other productions then define precisely what an expr is and what else a stmt can be.

This section reviews the definition of a context-free grammar and introduces terminology for talking about parsing. In particular, the notion of derivations is very helpful for discussing the order in which productions are applied during parsing.

1. The Formal Definition of a Context-Free Grammar

From Section 2.2, a context-free grammar (grammar for short) consists of terminals, nonterminals, a start symbol, and productions.

            Terminals are the basic symbols from which strings are formed. The term "token name" is a synonym for "terminal" and frequently we will use the

word "token" for terminal when it is clear that we are talking about just the token name. We assume that the terminals are the first components of the tokens output by the lexical analyzer. In (4.4), the terminals are the keywords if and else and the symbols "(" and " ) . "

            Nonterminals are syntactic variables that denote sets of strings. In (4.4), stmt and expr are nonterminals. The sets of strings denoted by nontermi-nals help define the language generated by the grammar. Nonterminals impose a hierarchical structure on the language that is key to syntax analysis and translation.

            In a grammar, one nonterminal is distinguished as the start symbol, and the set of strings it denotes is the language generated by the grammar. Conventionally, the productions for the start symbol are listed first.

            The productions of a grammar specify the manner in which the termi-nals and nonterminals can be combined to form strings. Each production consists of:

            A nonterminal called the head or left side of the production; this production defines some of the strings denoted by the head.

(b)  The symbol -K  Sometimes  : : = has been used in place of the arrow.

A body or right side consisting of zero or more terminals and non-terminals. The components of the body describe one way in which strings of the nonterminal at the head can be constructed.

Example     4.5 :  The grammar in Fig. 4.2 defines simple arithmetic expressions. In this grammar, the terminal symbols are  

i d +  -        *        /         (        )

The nonterminal symbols are expression, term and factor, and expression is the start symbol •

expression   ->      expression +         term

expression       ->         expression - term

expression   ->      term                     

term   ->      term   *        factor

term     ->    term   /         factor

term    ->    factor                   

factor       ->      ( expression )

factor ->      i d                        

 Figure 4.2:  Grammar for simple arithmetic expressions

2. Notational Conventions

To avoid always having to state that "these are the terminals," "these are the nonterminals," and so on, the following notational conventions for grammars will be used throughout the remainder of this book.

            These symbols are terminals:

                               Lowercase letters early in the alphabet, such as a, b, c.

                               Operator symbols such as +, *, and so on.

                               Punctuation symbols such as parentheses, comma, and so on.

            The digits 0 , 1 , . . . ,9 .

                               Boldface strings such as id or if, each of which represents a single terminal symbol.

            These symbols are nonterminals:

                               Uppercase letters early in the alphabet, such as A, B, C.

                               The letter S, which, when it appears, is usually the start symbol.

                              Lowercase, italic names such as expr or stmt.

                              When discussing programming constructs, uppercase letters may be used to represent nonterminals for the constructs. For example, non-terminals for expressions, terms, and factors are often represented by E, T, and F, respectively.

                              Uppercase letters late in the alphabet, such as X, 7, Z, represent grammar symbols; that is, either nonterminals or terminals.

                              4. Lowercase letters late in the alphabet, chiefly u,v,..., z, represent (possibly empty) strings of terminals.

                              5. Lowercase Greek letters, a, 0, 7 for example, represent (possibly empty) strings of grammar symbols. Thus, a generic production can be written as A ->• a, where A is the head and a the body.

                              6. A set of productions A -» ai, A -»• a2,... , A -> ak with a common head

                              A (call them A-productions), may be written A ->• a1 | 0:2 | • • • | 0 ^ . Call

                              a i , « 2 5 • • • ? c K f c the alternatives for A.

                              Unless stated otherwise, the head of the first production is the start sym-bol.

                              Exam p l e 4 .6 : Using these conventions, the grammar of Example 4.5 can be rewritten concisely as

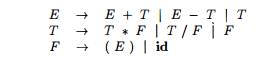
                              The notational conventions tell us that E, T, and F are nonterminals, with E the start symbol. The remaining symbols are terminals. •

3. Derivations

The construction of a parse tree can be made precise by taking a derivational view, in which productions are treated as rewriting rules. Beginning with the start symbol, each rewriting step replaces a nonterminal by the body of one of its productions. This derivational view corresponds to the top-down construction of a parse tree, but the precision afforded by derivations will be especially helpful when bottom-up parsing is discussed. As we shall see, bottom-up parsing is related to a class of derivations known as "rightmost" derivations, in which the rightmost nonterminal is rewritten at each step.

For example, consider the following grammar, with a single nonterminal E, which adds a production E ->• — E to the grammar (4.3):

            which is read, "E derives —E." The production E -> ( E ) can be applied to replace any instance of E in any string of grammar symbols by (E), e.g., E* E (E) *E or E*E=>E* (E). We can take a single E and repeatedly apply productions in any order to get a sequence of replacements. For example,

             E=>-E=>-(E) => - ( i d )

            We call such a sequence of replacements a derivation of - ( i d ) from E. This derivation provides a proof that the string - ( i d ) is one particular instance of an expression.

            For a general definition of derivation, consider a nonterminal A in the middle of a sequence of grammar symbols, as in aA(3, where . a and (3 are arbitrary strings of grammar symbols. Suppose A ->• 7 is a production. Then, we write aAj3 aj(3. The symbol means, "derives in one step." When a sequence of derivation steps a1 =>• a2 => • • • an rewrites a± to an, we say at derives an. Often, we wish to say, "derives in zero or more steps." For this purpose, we can use the symbol =>•. Thus,

     where S is the start symbol of a grammar G, we say that a is a sentential form of G. Note that a sentential form may contain both terminals and nonterminals, and may be empty. A sentence of G is a sentential form with no nonterminals. The language generated by a grammar is its set of sentences. Thus, a string of terminals w is in L(G), the language generated by G, if and only if w is a sentence of G (or S =>• w). A language that can be generated by a grammar is said to be a context-free language. If two grammars generate the same language, the grammars are said to be equivalent.

            The string - ( i d + id) is a sentence of grammar (4.7) because there is a derivation

            The strings E, -E, -(E),... , - (id + id) are all sentential forms of this grammar. We write E ^ - ( i d + id) to indicate that - ( i d + id) can be derived from E.

            At each step in a derivation, there are two choices to be made. We need to choose which nonterminal to replace, and having made this choice, we must pick a production with that nonterminal as head. For example, the following alternative derivation of - ( i d + id) differs from derivation (4.8) in the last two steps:

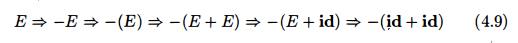
            Each nonterminal is replaced by the same body in the two derivations, but the order of replacements is different.

            To understand how parsers work, we shall consider derivations in which the nonterminal to be replaced at each step is chosen as follows:

            Analogous definitions hold for rightmost derivations. Rightmost derivations are sometimes called canonical derivations.

4. Parse Trees and Derivations

            A parse tree is a graphical representation of a derivation that filters out the order in which productions are applied to replace nonterminals. Each interior node of a parse tree represents the application of a production. The interior node is labeled with the nonterminal A in the head of the production; the children of the node are labeled, from left to right, by the symbols in the body of the production by which this A was replaced during the derivation.

            For example, the parse tree for - ( i d + id) in Fig. 4.3, results from the derivation (4.8) as well as derivation (4.9).

            The leaves of a parse tree are labeled by nonterminals or terminals and, read from left to right, constitute a sentential form, called the yield or frontier of the tree.

            To see the relationship between derivations and parse trees, consider any derivation  is a single nonterminal A. For each sentential form at in the derivation, we can construct a parse tree whose yield is ai. The process is an induction on i.

            BASIS: The tree for a1 = A is a single node labeled A.

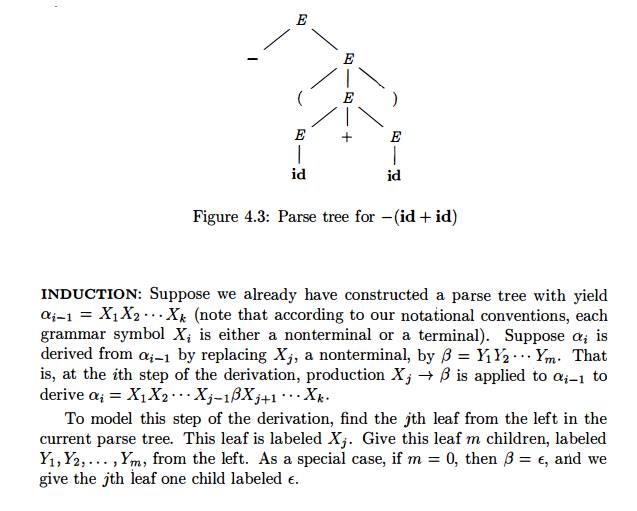
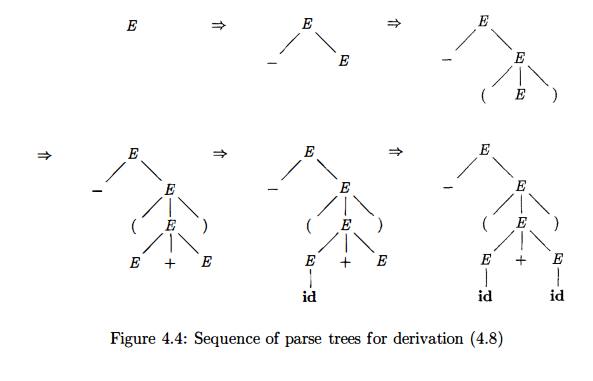
            Example 4.10 : The sequence of parse trees constructed from the derivation (4.8) is shown in Fig. 4.4. In the first step of the derivation, E -E. To model this step, add two children, labeled — and E, to the root E of the initial tree. The result is the second tree.

            In the second step of the derivation, —E =$> -(E). Consequently, add three children, labeled (_j E, and ), to the leaf labeled E of the second tree, to obtain the third tree with yield -(E). Continuing in this fashion we obtain the complete parse tree as the sixth tree. •

            Since a parse tree ignores variations in the order in which symbols in senten-tial forms are replaced, there is a many-to-one relationship between derivations and parse trees. For example, both derivations (4.8) and (4.9), are associated with the same final parse tree of Fig. 4.4.

            In what follows, we shall frequently parse by producing a leftmost or a rightmost derivation, since there is a one-to-one relationship between parse trees and either leftmost or rightmost derivations. Both leftmost and rightmost derivations pick a particular order for replacing symbols in sentential forms, so they too filter out variations in the order. It is not hard to show that every parse tree has associated with it a unique leftmost and a unique rightmost derivation.

5. Ambiguity

From Section 2.2.4, a grammar that produces more than one parse tree for some sentence is said to be ambiguous. P u t another way, an ambiguous grammar is one that produces more than one leftmost derivation or more than one rightmost derivation for the same sentence.

E x a m p l e 4 . 1 1 : The arithmetic expression grammar (4.3) permits two distinct leftmost derivations for the sentence id + id * id:

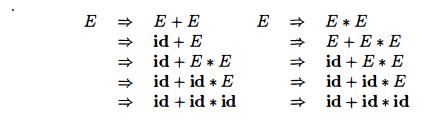
The corresponding parse trees appear in Fig. 4.5.

Note that the parse tree of Fig. 4.5(a) reflects the commonly assumed prece-dence of + and *, while the tree of Fig. 4.5(b) does not. That is, it is customary to treat operator * as having higher precedence than +, corresponding to the fact that we would normally evaluate an expression like a + b * c as a + (b * c), rather than as (a + b) * c. •

For most parsers, it is desirable that the grammar be made unambiguous, for if it is not, we cannot uniquely determine which parse tree to select for a sentence. In other cases, it is convenient to use carefully chosen ambiguous grammars, together with disambiguating rules that "throw away" undesirable parse trees, leaving only one tree for each sentence.

6. Verifying the Language Generated by a Grammar

Although compiler designers rarely do so for a complete programming-language grammar, it is useful to be able to reason that a given set of productions gener-ates a particular language. Troublesome constructs can be studied by writing a concise, abstract grammar and studying the language that it generates. We shall construct such a grammar for conditional statements below.

A proof that a grammar G generates a language L has two parts: show that every string generated by G is in L, and conversely that every string in L can indeed be generated by G.

Example 4.12 :  Consider the following grammar:       

It may not be initially apparent, but this simple grammar generates all strings of balanced parentheses, and only such strings. To see why, we shall show first that every sentence derivable from S is balanced, and then that every balanced string is derivable from 5. To show that every sentence derivable from S is balanced, we use an inductive proof on the number of steps n in a derivation.

BASIS: The basis is n = 1. The only string of terminals derivable from S in one step is the empty string, which surely is balanced.

INDUCTION : Now assume that all derivations of fewer than n steps produce balanced sentences, and consider a leftmost derivation of exactly n steps. Such a derivation must be of the form

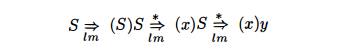
The derivations of x and y from S take fewer than n steps, so by the inductive hypothesis x and y are balanced. Therefore, the string (x)y must be balanced. That is, it has an equal number of left and right parentheses, and every prefix has at least as many left parentheses as right.

Having thus shown that any string derivable from S is balanced, we must next show that every balanced string is derivable from S. To do so, use induction on the length of a string.

B A S I S: If the string is of length 0, it must be e, which is balanced.

I N D U C T I O N : First, observe that every balanced string has even length. As-sume that every balanced string of length less than 2n is derivable from 5, and consider a balanced string w of length 2n, n > 1. Surely w begins with a left parenthesis. Let (x) be the shortest nonempty prefix of w having an equal number of left and right parentheses. Then w can be written as w = (x)y where both x and y are balanced. Since x and y are of length less than 2n, they are derivable from S by the inductive hypothesis. Thus, we can find a derivation of the form

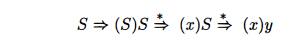
proving that w = (x)y is also derivable from 5.    •

7. Context-Free Grammars Versus Regular Expressions

Before leaving this section on grammars and their properties, we establish that grammars are a more powerful notation than regular expressions. Every con-struct that can be described by a regular expression can be described by a gram-mar, but not vice-versa. Alternatively, every regular language is a context-free language, but not vice-versa.

For example, the regular expression (a|b)*abb and the grammar

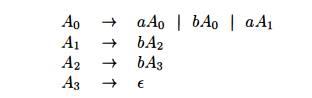
describe the same language, the set of strings of a's and 6's ending in abb.

We can construct mechanically a grammar to recognize the same language as a nondeterministic finite automaton (NFA). The grammar above was con-structed from the NFA in Fig. 3.24 using the following construction:

1. For each state i of the NFA, create a nonterminal Ai.

            If state i has a transition to state j on input a, add the production Ai —> aAj. If state i goes to state j on input e, add the production Ai —• Aj.

            Hi is an accepting state, add Ai —> e.

If i is the start state, make Ai be the start symbol of the grammar.

On the other hand, the language L =  {aⁿbⁿ | n >= 1}with an equal number of a's and 6's is a prototypical example of a language that can be described by a grammar but not by a regular expression. To see why, suppose L were the language defined by some regular expression. We could construct a DFA D with a finite number of states, say k, to accept L. Since D has only k states, for an input beginning with more than k a's, D must enter some state twice, say Si, as in Fig. 4.6. Suppose that the path from Si back to itself is labeled with a sequence aⁱbⁱ Since a1 bl is in the language, there must be a path labeled bl from Si to an accepting state /. But, then there is also a path from the initial state «o through to / labeled aⁱbⁱ, as shown in Fig. 4.6. Thus, D also accepts aⁱbⁱ, which is not in the language, contradicting the assumption that L is the language accepted by D.

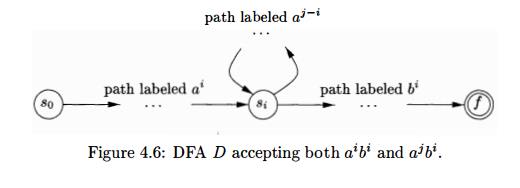
Colloquially, we say that "finite automata cannot count," meaning that a finite automaton cannot accept a language like {anbn1n > 1} that would require it to keep count of the number of a's before it sees the 6's. Likewise, "a grammar can count two items but not three," as we shall see when we consider non-context-free language constructs in Section 4.3.5.

8. Exercises for Section 4.2

Exercis 4 . 2 . 1 :  Consider the context-free grammar:

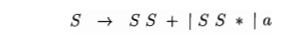
and the string aa + a*.

            Give a leftmost derivation for the string.

            Give a rightmost derivation for the string.

            Give a parse tree for the string.

! d)  Is the grammar ambiguous or unambiguous? Justify your answer.

! e)  Describe the language generated by this grammar.

Exercise 4 . 2 . 2 :  Repeat Exercise 4.2.1 for each of the following grammars and strings:

Exercise 4 . 2 . 3 :  Design grammars for the following languages:

a) The set of all strings of 0s and Is such that every 0 is immediately followed by at least one 1.

! b) The set of all strings of 0s and Is that are palindromes; that is, the string reads the same backward as forward.

! c)  The set of all strings of 0s and Is with an equal number of 0s and Is.

!! d) The set of all strings of 0s and Is with an unequal number of 0s and Is.

! e) The set of all strings of 0s and Is in which Oil does not appear as a substring.

!! f) The set of all strings of 0s and Is of the form xy, where x ^ y and x and y are of the same length.

Exercise 4 . 2 . 4 : There is an extended grammar notation in common use. In this notation, square and curly braces in production bodies are metasymbols (like —>• or |) with the following meanings:

i) Square braces around a grammar symbol or symbols denotes that these constructs are optional. Thus, production A —> X [Y] Z has the same effect as the two productions A X Y Z and A -± X Z.

ii) Curly braces around a grammar symbol or symbols says that these symbols may be repeated any number of times, including zero times. Thus,

 A —>• X {Y Z} has the same effect as the infinite sequence of productions A-*X,A->XYZ,A-*XYZYZ, and so on.

Show that these two extensions do not add power to grammars; that is, any language that can be generated by a grammar with these extensions can be generated by a grammar without the extensions.

Exercise 4.2.5 :  Use the braces described in Exercise 4.2.4 to  simplify the following grammar for statement blocks and conditional statements:

      Exercise 4 . 2 . 6 : Extend the idea of Exercise 4.2.4 to allow any regular expres-sion of grammar symbols in the body of a production. Show that this extension does not allow grammars to define any new languages.

      Exercise 4 . 2 . 7:  A grammar symbol X (terminal or nonterminal) is useless if there is no derivation of the form S wXy  ^ wxy. That is,  X  can never  appear in the derivation of any sentence.

            Give an algorithm to eliminate from a grammar all productions containing useless symbols.

            Apply your algorithm to the grammar:

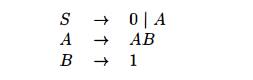
             Exercise 4 . 2 . 8:     The grammar in  Fig.  4.7 generates declarations for a single numerical identifier; these declarations involve four different, independent properties of numbers.

Figure 4.7:  A grammar for multi-attribute declarations

a) Generalize the grammar of Fig. 4.7 by allowing n options Ai, for some fixed n and for i = 1,2 ... ,n, where Ai can be either ai or bi. Your grammar should use only 0(n) grammar symbols and have a total length of productions that is 0(n).

! b) The grammar of Fig. 4.7 and its generalization in part (a) allow declara-tions that are contradictory and/or redundant, such as:

declare foo real fixed real floating

We could insist that the syntax of the language forbid such declarations; that is, every declaration generated by the grammar has exactly one value for each of the n options. If we do, then for any fixed n there is only a finite number of legal declarations. The language of legal declarations thus has a grammar (and also a regular expression), as any finite language does. The obvious grammar, in which the start symbol has a production for every legal declaration has n! productions and a total production length of 0 ( n x n!). You must do better: a total production length that is 0 ( n 2 n ) .

!! c) Show that any grammar for part (b) must have a total production length of at least 2 n .

d) What does part (c) say about the feasibility of enforcing nonredundancy and noncontradiction among options in declarations via the syntax of the programming language?