Chapter: Compilers : Principles, Techniques, & Tools : Syntax Analysis
Introduction to LR Parsing: Simple LR
Introduction to LR Parsing:
Simple LR
1 Why LR Parsers?
2 Items and the LR(0) Automaton
3 The LR-Parsing Algorithm
4 Constructing SLR-Parsing Tables
5 Viable Prefixes
6 Exercises for Section 4.6
The most prevalent type of bottom-up parser today is based on a concept
called LR(fc) parsing; the "L" is for left-to-right scanning of the
input, the "R" for constructing a rightmost derivation in reverse,
and the k for the number of input
symbols of lookahead that are used in making parsing decisions. The cases k = 0 or k = 1 are of practical interest, and we shall only consider LR parsers
with k < 1 here. When (k) is omitted, k is assumed to be 1.
This section introduces the basic concepts of LR parsing and the easiest
method for constructing shift-reduce parsers, called "simple LR" (or
SLR, for short). Some familiarity with the basic concepts is helpful even if
the LR parser itself is constructed using an automatic parser generator. We
begin with "items" and "parser states;" the diagnostic
output from an LR parser generator typically includes parser states, which can
be used to isolate the sources of parsing conflicts.
Section 4.7 introduces two, more complex methods — canonical-LR and LALR
— that are used in the majority of LR parsers.
1. Why LR Parsers?
LR parsers are table-driven, much like the nonrecursive LL parsers of
Sec-tion 4.4.4. A grammar for which we can construct a parsing table using one
of the methods in this section and the next is said to be an LR grammar. Intu-itively, for a grammar
to be LR it is sufficient that a left-to-right shift-reduce parser be able to
recognize handles of right-sentential forms when they appear on top of the
stack.
LR
parsing is attractive for a variety of reasons:
LR parsers can be constructed to
recognize virtually all programming-language constructs for which context-free
grammars can be written. Non-LR context-free grammars exist, but these can
generally be avoided for typical programming-language constructs.
The LR-parsing method is the most
general nonbacktracking shift-reduce parsing method known, yet it can be
implemented as efficiently as other,
more
primitive shift-reduce methods (see the bibliographic notes).
An LR parser can detect a
syntactic error as soon as it is possible to do so on a left-to-right scan of
the input.
The class of grammars that can be
parsed using LR methods is a proper superset of the class of grammars that can
be parsed with predictive or LL methods. For a grammar to be LR(fc), we must be
able to recognize the occurrence of the right side of a production in a
right-sentential form, with k input
symbols of lookahead. This requirement is far less stringent than that for
LL(ife) grammars where we must be able to recognize the use of a production
seeing only the first k symbols of
what its right side derives. Thus, it should not be surprising that LR grammars
can describe more languages than LL grammars.
The principal drawback of the LR method is that it is too much work to
construct an LR parser by hand for a typical programming-language grammar. A
specialized tool, an LR parser generator, is needed. Fortunately, many such
generators are available, and we shall discuss one of the most commonly used
ones, Yacc, in Section 4.9. Such a
generator takes a context-free grammar and automatically produces a parser for
that grammar. If the grammar contains ambiguities or other constructs that are
difficult to parse in a left-to-right scan of the input, then the parser
generator locates these constructs and provides detailed diagnostic messages.
2. Items and the LR(O) Automaton
How does a shift-reduce parser know when to shift and when to reduce?
For example, with stack contents $ T and next input symbol * in Fig. 4.28, how
does the parser know that T on the top of the stack is not a handle, so the
appropriate action is to shift and not to reduce TtoEP.
An LR parser makes shift-reduce decisions by maintaining states to keep
track of where we are in a parse. States represent sets of "items."
An LR(0) item (item for short) of a grammar G is a production of G with a dot
at some position of the body. Thus, production A XYZ yields the four items
A -XYZ
A -+ XYZ
A -> XYZ
A XYZ-
The production A ->• e generates only one item, A .
Intuitively, an item indicates how much of a production we have seen at
a given point in the parsing process. For example, the item A -» XYZ indicates
that we hope to see a string derivable from XYZ next on the input. Item
Representing Item Sets
A parser generator that produces a bottom-up parser may need to
rep-resent items and sets of items conveniently. Note that an item can be
represented by a pair of integers, the first of which is the number of one of
the productions of the underlying grammar, and the second of which is the
position of the dot. Sets of items can be represented by a list of these pairs.
However, as we shall see, the necessary sets of items often include
"closure" items, where the dot is at the beginning of the body. These
can always be reconstructed from the other items in the set, and we do not have
to include them in the list.
A -» XYZ indicates that we have just seen on the input a string derivable from X and that we hope next to see a string
derivable from YZ. Item A —> XYZ-indicates that we have seen
the body XYZ and that it may be time
to reduce
XYZ to A.
One collection of sets of LR(0) items, called the canonical LR(0) collection, provides the basis for constructing a
deterministic finite automaton that is used to make parsing decisions. Such an
automaton is called an LR(0) automaton.3 In particular, each state of the LR(0) automaton represents a set of
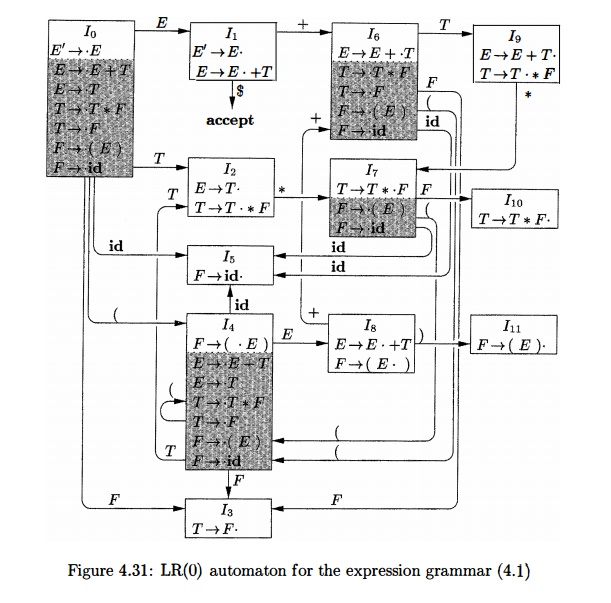
items in the canonical LR(0) collection. The automaton for the expression
grammar (4.1), shown in Fig. 4.31, will serve as the running example for
discussing the canonical LR(0) collection for a grammar.
To construct the canonical LR(0) collection for a grammar, we define an
augmented grammar and two functions, CLOSURE and GOTO . If G is a grammar with start symbol S, then G', the augmented
grammar for G, is G with a new
start symbol 5" and production S'
—> S. The purpose of this new starting production is to indicate to the
parser when it should stop parsing and announce acceptance of the input. That
is, acceptance occurs when and only when the parser is about to reduce by S' -» S.
Closure of
Item Sets
If I is a set of items for a grammar G,
then CLOSURE(I) is the set of items constructed from / by the two rules:
Initially, add every item in / to
CLOSURE(Z).
If A -» a-B/3 is in
CLOSURE(J) and B ->• 7 is a
production, then add the item B -7 to
CLOSURE(7), if it is not already there. Apply this rule until no more new items
can be added to CLOSURE(J).

Example 4.40 : Consider the augmented expression grammar:
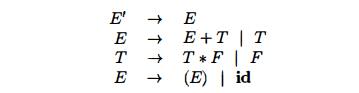
If I is the set of one item {[E' -»• -E]}, then CLOSURE(J) contains the
set of items I0 in Fig. 4.31.
To see how the closure is
computed, E' -»• E is put in C L O S U R E ( J ) by rule
(1). Since there is an E immediately to the right of a dot, we add the E-productions with dots at the
left ends: E -E + T and E ->• T. Now
there is a T immediately to the right of a dot in the latter item, so we add T
-> T*F and T -> F. Next, the F to the right of a dot forces us to add F
->• -(E) and F -» -id, but no other items need to be added. •
The closure can be computed as in Fig. 4.32. A convenient way to imple-ment the function closure is to keep a boolean array added, indexed by the nonterminals of G, such that added[B] is set to true if and when we add the item item b -- > .'g for each B-production b -- > 'g.

Moreover, each set of items of interest is formed by taking the closure
of a set of kernel items; the items added in the closure can never be kernel
items, of course. Thus, we can represent the sets of items we are really
interested in with very little storage if we throw away all nonkernel items,
knowing that they could be regenerated by the closure process. In Fig. 4.31,
nonkernel items are in the shaded part of the box for a state.
The Function
GOTO
The second useful function is GOTO (I, X) where I is a set of items and
X is a grammar symbol. GOTO (I, X) is
defined to be the closure of the set of all items [A -> aX-b] such
that [A -> a • Xb] is in I.
Intuitively, the GOTO function is used to define the transitions in the LR(0)
automaton for a grammar. The states of the automaton correspond to sets of
items, and GOTO(I,X) specifies the transition from the state for I under input
X.

We are now ready for the algorithm to construct C, the canonical
collection of sets of LR(0) items for an augmented grammar G' — the algorithm
is shown in Fig. 4.33.
void items(G') {
C = CLOSURE({[S' -> S]}); repeat
for ( each set of items I in C )
for ( each grammar symbol X )
if ( GOTO (I, X) is not empty and
not in C )
add GOTO(I, X) to C;
until no new sets of items are added to C on a round;
}
Figure 4.33: Computation of the
canonical collection of sets of LR(0) items
Example 4.42 : The canonical collection of sets
of LR(0) items for grammar (4.1) and the GOTO function are shown in Fig. 4.31.
GOTO is encoded by the transitions in the figure. •
Use of the LR(O)
Automaton
The central idea behind "Simple LR," or SLR, parsing is the
construction from the grammar of the LR(0) automaton. The states of this
automaton are the sets of items from the canonical LR(0) collection, and the
transitions are given by the G O T O
function. The LR(0) automaton for the expression grammar (4.1) appeared earlier
in Fig. 4.31.
The start state of the LR(0) automaton is C L O S U R E ( { [ S' ->• S]}), where S' is the start symbol of the augmented grammar. All states are
accepting states. We say "state j" to refer to the state
corresponding to the set of items Ij.
How can LR(0) automata help with shift-reduce decisions? Shift-reduce
decisions can be made as follows. Suppose that the string 7 of grammar symbols
takes the LR(0) automaton from the start state 0 to some state j. Then, shift on next input symbol a if state j has a transition on a.
Otherwise, we choose to reduce; the items in state j will tell us which production to use.
The LR-parsing algorithm to be introduced in Section 4.6.3 uses its
stack to keep track of states as well as grammar symbols; in fact, the grammar
symbol can be recovered from the state, so the stack holds states. The next
example gives a preview of how an LR(0) automaton and a stack of states can be
used to make shift-reduce parsing decisions.
Example 4.43 : Figure 4.34 illustrates the actions of a shift-reduce parser
on input id * id, using the LR(0) automaton in Fig. 4.31. We use a stack to
hold states; for clarity, the grammar symbols corresponding to the states on
the stack appear in column S Y M B O L S . At line (1), the stack holds the
start state 0 of the automaton; the corresponding symbol is the bottom-of-stack
marker $.

The next input symbol is id
and state 0 has a transition on id
to state 5. We therefore shift. At line (2), state 5 (symbol id) has been pushed onto the stack.
There is no transition from state 5 on input *, so we reduce. From item [F -»
id] in state 5, the reduction is
by production F ->• id.
With symbols, a reduction is implemented by popping the body of the
pro-duction from the stack (on line (2), the body is id) and pushing the head of the production (in this case, F). With states, we pop state 5 for
symbol id, which brings state 0 to
the top and look for a transition on F,
the head of the production. In Fig. 4.31, state 0 has a transition on F to state 3, so we push state 3, with
corresponding symbol F; see line (3).
As another example, consider line (5), with state 7 (symbol *) on top of
the stack. This state has a transition to state 5 on input id, so we push state 5 (symbol id).
State 5 has no transitions, so we reduce by F
—> id. When we pop state 5
for the body id, state 7 comes to the top of the stack. Since state 7 has a
transition on F to state 10, we push state 10 (symbol F).
3. The LR-Parsing Algorithm
A schematic of an LR parser is shown in Fig. 4.35. It consists of an
input, an output, a stack, a driver program, and a parsing table that has two
parts (ACTION and GOTO). The driver program is the same for all LR parsers;
only the parsing table changes from one parser to another. The parsing program
reads characters from an input buffer one at a time. Where a shift-reduce
parser would shift a symbol, an LR parser shifts a state. Each state summarizes the information contained in the stack
below it.
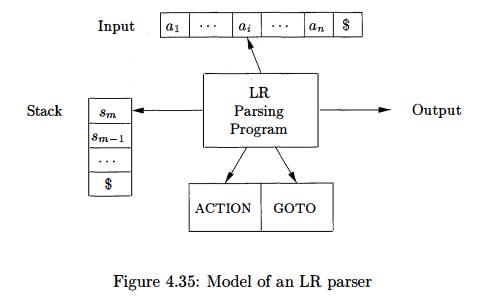
The stack holds a sequence of states, sosi • • • sm, where sm is on top. In the SLR method, the stack holds states from the LR(0)
automaton; the canonical-LR and LALR methods are similar. By construction, each
state has a corre-sponding grammar symbol. Recall that states correspond to
sets of items, and that there is a transition from state i to state j if GOTO(Ii,X) = Ij. All tran-sitions to
state j must be for the same grammar
symbol X. Thus, each state, except
the start state 0, has a unique grammar symbol associated with it . 4
Structure of
the LR Parsing Table
The
parsing table consists of two parts: a parsing-action function ACTION and a
goto function GOTO.
1. The ACTION function takes as arguments a state i and a terminal a (or $,
the input endmarker). The value of ACTION[i,a] can have one of four forms:
Shift j, where j is a state.
The action taken by the parser effectively shifts input a to the stack, but uses state j
to represent a.
Reduce A-> b. The action of the parser effectively reduces b on the top of the stack to head A.
Accept. The parser accepts the input and finishes
parsing.
Error. The parser discovers an
error in its input and takes some corrective action. We shall have more to say
about how such error-recovery routines work in Sections 4.8.3 and 4.9.4.
We extend the GOTO function,
defined on sets of items, to states: if GOTO[/i, A] = Ij, then GOTO also maps a state i and a nonterminal A to
state j .
LR - Parser Configurations
To describe the behavior of an LR parser, it helps to have a notation
repre-senting the complete state of the parser: its stack and the remaining
input. A configuration of ah LR
parser is a pair:
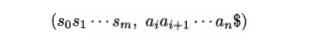
where the first component is the stack contents (top on the right), and
the second component is the remaining input. This configuration represents the
right-sentential form
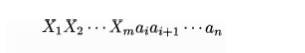
in essentially the same way as a shift-reduce parser would; the only
difference is that instead of grammar symbols, the stack holds states from
which grammar symbols can be recovered. That is, X{ is the grammar symbol
represented by state Si. Note that s0, the start state of the parser, does not represent a grammar symbol, and
serves as a bottom-of-stack marker, as well as playing an important role in the
parse.
Behavir of
the LR Parser
The next move of the parser from the configuration above is determined
by reading a*, the current input symbol, and s m , the state on top of the stack,
and then consulting the entry A C T I O N [ s m , a*] in the
parsing action table. The configurations resulting after each of the four types
of move are as follows
1. If
ACTION[s m ,ai] = shift s, the parser executes a
shift move; it shifts the next state
s
onto the stack, entering the configuration

The symbol ai need not be held on the stack, since it can be recovered
from s, if needed (which in practice it never is). The current input symbol is now a
j + i .
2. If ACTION [sm, ai] = reduce
A -> b, then the parser executes a reduce
move, entering the configuration
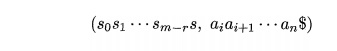
where r is
the length of 0, and s = GOTO[sm-r, A]. Here the parser first popped r
state symbols off the stack, exposing state s T O _ r . The
parser then pushed s, the entry for G O
T O [ s m _ r , A], onto the stack. The
current input symbol is not changed in a reduce move. For the LR parsers we shall construct, Xm-r+i-'Xm,
the sequence of
grammar symbols corresponding to
the states popped off the stack,
will always match (3, the right side of the
reducing production.
The output of an LR parser is generated after a reduce move by executing
the semantic action associated with the reducing production. For the time
being, we shall assume the output consists of just printing the reducing
production.
3. If ACTlON [ s m , ai1 = accept, parsing is completed.
4. If ACTlON [ s m , ai1 = error, the parser has discovered an error and
calls an error recovery routine.
The LR-parsing algorithm is
summarized below. All LR parsers behave in this fashion; the only
difference between one LR parser and another is the information in the ACTION
and GOTO fields of the parsing table.
Algorithm 4.44 : LR-parsing algorithm.
INPUT : An input string w and an LR-parsing table with functions ACTION and
grammar G. GOTO for a
OUTPUT : If w is in L(G), the reduction steps of a bottom-up parse for w;
otherwise, an error indication.
METHOD : Initially, the parser has s0 on its stack, where s0 is the initial
state, and w$ in the input buffer. The parser then executes the program in Fig.
4.36.
let a be the first symbol of w$;
w h i l e(1) { /* repeat
forever */
let s be the state on top of the stack;
if ( ACTION[s, a] = shift t ) {
push t onto the stack;
let a be the next input symbol;
} else if ( ACTION [s, a] = reduce A (3 ) { pop 1{31 symbols off the
stack;
let state t now be on top of the stack; push GOTOft, A] onto the stack;
output the production A -» /?;
} else if ( ACTION[s,a] = accept ) break; /* parsing is done */ else
call error-recovery routine;
}
Figure 4.36: LR-parsing program
Example 4 . 4 5 : Figure 4.37 shows the ACTION and GOTO functions of an LR-parsing table
for the expression grammar (4.1), repeated here with the productions numbered:
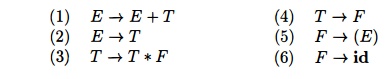
The codes
for the actions are:
1. si means shift and stack state z,
2. rj means reduce by the production
numbered j,
acc means accept,
blank means error.
Note that the value of GOTO[s,
a] for terminal a is found in the ACTION
field connected with the shift action on input a for state s. The GOTO field gives GOTOJs, A] for
nonterminals A. Although we have not
yet explained how the entries for Fig. 4.37 were selected, we shall deal with
this issue shortly.
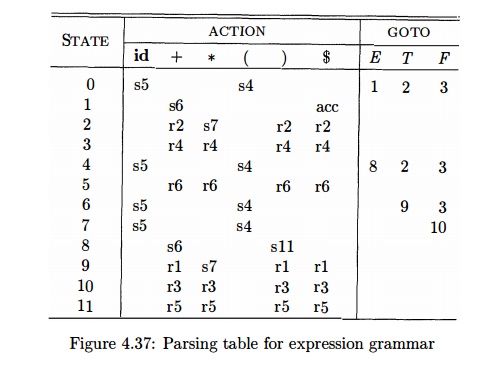
On input id * id + id, the sequence of stack and input contents is shown
in Fig. 4.38. Also shown for clarity, are the sequences of grammar symbols
corresponding to the states held on the stack. For example, at line (1) the LR
parser is in state 0, the initial state with no grammar symbol, and with id the
first input symbol. The action in row 0 and column id of the action field of
Fig. 4.37 is s5, meaning shift by pushing state 5. That is what has happened at
line (2): the state symbol 5 has been pushed onto the stack, and id has been
removed from the input.
Then, * becomes the current input symbol, and the action of state 5 on
input * is to reduce by F id. One state
symbol is popped off the stack. State 0
is then exposed. Since the goto of state 0 on F is 3, state 3 is pushed onto
the stack. We now have the configuration in line (3). Each of the remaining
moves is determined similarly.
4. Constructing SLR-Parsing
Tables
The SLR method for constructing parsing tables is a good starting point
for studying LR parsing. We shall refer to the parsing table constructed by
this method as an SLR table, and to an LR parser using an SLR-parsing table as
an SLR parser. The other two methods augment the SLR method with lookahead
information.
The SLR method begins with LR(0) items and LR(0) automata, introduced in
Section 4.5. That is, given a grammar, G,
we augment G to produce G', with a new start symbol S'. From G', we construct C, the canonical collection of sets of items for G' together with the G O T O function.

The ACTION and GOTO entries in the parsing table are then constructed
using the following algorithm. It requires us to know FOLLOW(A) for each
nonterminal A of a grammar (see Section 4.4).
Algorith m 4 . 4 6 : Constructing an SLR-parsing table.
INPUT : An augmented grammar G'.
OUTPUT : The SLR-parsing table functions ACTION and GOTO for G'.
METHOD :

If any conflicting actions result from the above rules, we say the
grammar is not SLR(l) . The algorithm fails to produce a parser in this case.

The parsing table consisting of the ACTION and GOTO functions determined
by Algorithm 4.46 is called the SLR(l)
table for G. An LR parser using the SLR(l) table for G is called the SLR(l) parser for G, and a grammar having an SLR(l) parsing table is said to be SLR(l). We usually omit the
"(1)" after the "SLR," since we shall not deal here with
parsers having more than one symbol of lookahead.
E x a m p l e 4 . 4 7 : Let us construct the SLR table for the augmented
expression grammar. The canonical collection of sets of LR(0) items for the
grammar was shown in Fig. 4.31. First consider the set of items Io:

Example 4.48 : Every SLR(l) grammar is unambiguous, but there are many
unambiguous grammars that are not SLR(l) . Consider the grammar with
pro-ductions
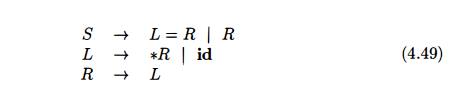
Think of L and R as standing for /-value and r-value, respectively, and
* as an operator indicating "contents of."5 The canonical collection
of sets of LR(0) items for grammar (4.49) is shown in Fig. 4.39.

Consider the set of items I2. The
first item in this set makes A C T I O N [ 2 , = ] be "shift 6."
Since F O L L O W ( J R ) contains = (to
see why, consider the derivation S L = R *R - R), the second item sets
ACTlON[2, =] to "reduce R -> L." Since there is both a shift and a
reduce entry in A C T I O N [ 2 , = ] , state 2 has a shift/reduce conflict on
input symbol =.
Grammar (4.49) is not ambiguous. This shift/reduce conflict arises from
the fact that the SLR parser construction method is not powerful enough to
remember enough left context to decide what action the parser should take on
input =, having seen a string reducible to L. The canonical and LALR methods,
to be discussed next, will succeed on a larger collection of grammars,
including 5 A s in Section 2.8.3, an /-value designates a location and an
r-value is a value that can be stored in a location.
grammar (4.49). Note, however, that there are unambiguous grammars for
which every LR parser construction method will produce a parsing action table
with parsing action conflicts. Fortunately, such grammars can generally be
avoided in programming language applications. •
5. Viable Prefixes
Why can LR(0) automata be used to make shift-reduce decisions? The LR(0)
automaton for a grammar characterizes the strings of grammar symbols that can
appear on the stack of a shift-reduce parser for the grammar. The stack
contents must be a prefix of a right-sentential form. If the stack holds a and the rest of the input is x, then a sequence of reductions will
take ax to S. In
Not all prefixes of
right-sentential forms can appear on the stack, however, since the parser must
not shift past the handle. For example, suppose
Then, at various times
during the parse, the stack will hold (, (E, and (E), but it must not hold
(E)*, since (E) is a handle, which the parser must reduce to F before shifting
*.
The prefixes of right
sentential forms that can appear on the stack of a shift-reduce parser are
called viable prefixes. They are defined as follows: a viable prefix is a
prefix of a right-sentential form that does not continue past the right end of
the rightmost handle of that sentential form. By this definition, it is always
possible to add terminal symbols to the end of a viable prefix to obtain a
right-sentential form.

We can easily compute
the set of valid items for each viable prefix that can appear on the stack of
an LR parser. In fact, it is a central theorem of LR-parsing theory
that the set of valid items for a viable prefix g is exactly the set
of items reached from the initial state along the path labeled g in the LR(0)
automaton for the grammar. In essence, the set of valid items embodies all
the useful information that can be gleaned from the stack. While we shall not
prove this theorem here, we shall give an example.

6. Exercises for Section 4.6
Exercise 4 . 6 . 1 : Describe all the viable prefixes
for the following grammars:
a) The grammar S 0 5 1 | 0 1 o f Exercise 4.2.2(a).
b) The grammar S - > S S + 1
S S * 1 a of Exercise 4.2.1.
c) The grammar S S ( S ) | e of Exercise 4.2.2(c).
Exercise 4 . 6 . 2 : Construct the SLR sets of items for the (augmented) grammar of Exercise
4;2.1. Compute the GOTO function for these sets of items. Show the parsing
table for this grammar. Is the grammar SLR?
Exercise 4 . 6 . 3 : Show the actions of your parsing table from Exercise 4.6.2 on the input
aa * a+.
Exercise 4 . 6 . 4 : For each of the (augmented)
grammars of Exercise 4.2.2(a)-
(g):
Construct the SLR sets of
items and their GOTO function.
Indicate any action
conflicts in your sets of items.
Construct the SLR-parsing
table, if one exists.
Exercise 4 . 6 . 5 : Show that
the following grammar:
S -» Aa Ab | B b B a
A -»• e
B -> e
is LL(1) but not SLR(l) .
Exercise 4 . 6 . 6 : Show that
the following grammar:
S S A | A
A -)• a
is SLR(l) but not LL(1).
Exercise 4 . 6 . 7: Consider the family of grammars
Gn defined by:
5 -» Ai bi for
1 < i < n
Ai -> aj Ai
| aj for 1 < i,j < n
and i ^ j
Show that:
a) Gn has 2 n 2 - n
productions.
b) Gn has 2n + n2 +
n sets of LR(0) items.
c) Gn is
SLR(l) .
What does this analysis say about how large LR parsers can get?
Exercise 4 . 6 . 8 : We suggested that individual items could be
regarded as states of a nondeterministic finite automaton, while sets of valid
items are the states of a deterministic finite automaton (see the box on
"Items as States of an NFA" in Section 4.6.5). For the grammar S S S
+ 1 S S * 1 a of Exercise 4.2.1:
a) Draw the transition diagram (NFA) for the valid items of this grammar
according to the rule given in the box cited above.
b) Apply the subset construction (Algorithm 3.20) to your NFA from part
(a). How does the resulting DFA compare to the set of LR(0) items for
the grammar?
c) Show that in all cases, the subset construction applied to the NFA
that comes from the valid items for a grammar produces the LR(0) sets of items.
Related Topics