Using Ambiguous Grammars

Using Ambiguous Grammars

1 Precedence and Associativity to Resolve Conflicts

2 The "Dangling-Else" Ambiguity

3 Error Recovery in LR Parsing

4 Exercises for Section 4.8

It is a fact that every ambiguous grammar fails to be LR and thus is not in any of the classes of grammars discussed in the previous two sections. How-ever, certain types of ambiguous grammars are quite useful in the specification and implementation of languages. For language constructs like expressions, an ambiguous grammar provides a shorter, more natural specification than any equivalent unambiguous grammar. Another use of ambiguous grammars is in isolating commonly occurring syntactic constructs for special-case optimiza-tion. With an ambiguous grammar, we can specify the special-case constructs by carefully adding new productions to the grammar.

Although the grammars we use are ambiguous, in all cases we specify dis-ambiguating rules that allow only one parse tree for each sentence. In this way, the overall language specification becomes unambiguous, and sometimes it be-comes possible to design an LR parser that follows the same ambiguity-resolving choices. We stress that ambiguous constructs should be used sparingly and in a strictly controlled fashion; otherwise, there can be no guarantee as to what language is recognized by a parser.

1. Precedence and Associativity to Resolve Conflicts

Consider the ambiguous grammar ( 4 . 3 ) for expressions with operators + and *, repeated here for convenience:

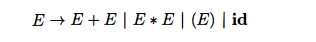
This grammar is ambiguous because it does not specify the associativity or precedence of the operators + and *. The unambiguous grammar ( 4 . 1 ) , which includes productions E -> E + T and T -> T*F, generates the same language, but gives + lower precedence than *, and makes both operators left associative. There are two reasons why we might prefer to use the ambiguous grammar. First, as we shall see, we can easily change the associativity and precedence of the operators + and * without disturbing the productions of ( 4 . 3 ) or the number of states in the resulting parser. Second, the parser for the unam-biguous grammar will spend a substantial fraction of its time reducing by the productions E -> T and T -> F, whose sole function is to enforce associativity and precedence. The parser for the ambiguous grammar ( 4 . 3 ) will not waste time reducing by these single productions (productions whose body consists of a single nonterminal).

The sets of L R ( 0 ) items for the ambiguous expression grammar ( 4 . 3 ) aug-mented by E' -> E are shown in Fig. 4 . 4 8 . Since grammar ( 4 . 3 ) is ambiguous, there will be parsing-action conflicts when we try to produce an LR parsing table from the sets of items. The states corresponding to sets of items Ij and Is generate these conflicts. Suppose we use the SLR approach to constructing the parsing action table. The conflict generated by I7 between reduction by E -> E + E and shift on + or * cannot be resolved, because + and * are each in F O L L O W ( £ ' ) . Thus both actions would be called for on inputs + and *. A similar conflict is generated by Is, between reduction by E -> E * E and shift on inputs + and *. In fact, each of our LR parsing table-construction methods will generate these conflicts.

However, these problems can be resolved using the precedence and associa-tivity information for + and *. Consider the input id + id * id, which causes a parser based on Fig. 4 . 4 8 to enter state 7 after processing id + id; in particular the parser reaches a configuration

For convenience, the symbols corresponding to the states 1, 4, and 7 are also shown under P R E F I X .

If * takes precedence over +, we know the parser should shift * onto the stack, preparing to reduce the * and its surrounding id symbols to an expression. This choice was made by the SLR parser of Fig. 4 . 3 7 , based on an unambiguous grammar for the same language. On the other hand, if + takes precedence over *, we know the parser should reduce E + E to E. Thus the relative precedence

Figure 4.48:  Sets of LR(0) items for an augmented expression grammar

of + followed by * uniquely determines how the parsing action conflict between reducing E -> E + E and shifting on * in state 7 should be resolved.

If the input had been id + id + id instead, the parser would still reach a configuration in which it had stack 0 14 7 after processing input id + id. On input + there is again a shift/reduce conflict in state 7. Now, however, the associativity of the + operator determines how this conflict should be resolved. If + is left associative, the correct action is to reduce by E —y E + E. That is, the id symbols surrounding the first + must be grouped first. Again this choice coincides with what the SLR parser for the unambiguous grammar would do.

In summary, assuming + is left associative, the action of state 7 on input + should be to reduce by E —> E + E , and assuming that * takes precedence over +, the action of state 7 on input * should be to shift. Similarly, assuming that * is left associative and takes precedence over +, we can argue that state 8, which can appear on top of the stack only when E * E are the top three grammar symbols, should have the action reduce E -> E * E on both + and * inputs. In the case of input +, the reason is that * takes precedence over +, while in the case of input *, the rationale is that * is left associative.

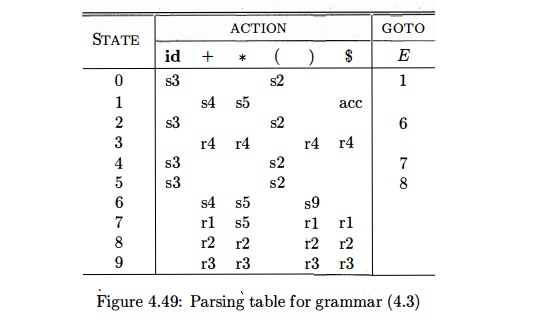
Proceeding in this way, we obtain the LR parsing table shown in Fig. 4.49. Productions 1 through 4 are E -> E + E, E ->• E * E, ->• (E), and E -» id, respectively. It is interesting that a similar parsing action table would be produced by eliminating the reductions by the single productions E -» T and T —»• F from the SLR table for the unambiguous expression grammar (4.1) shown in Fig. 4.37. Ambiguous grammars like the one for expressions can be handled in a similar way in the context of LALR and canonical LR parsing.

2. The "Dangling-Else" Ambiguity

Consider again the following grammar for conditional statements:

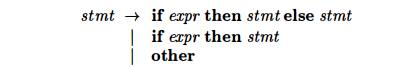
As we noted in Section 4.3.2, this grammar is ambiguous because it does not resolve the dangling-else ambiguity. To simplify the discussion, let us consider an abstraction of this grammar, where i stands for if expr then, e stands for else, and a stands for "all other productions."       We can then write the grammar, with augmenting production S' -- > S, as

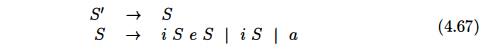
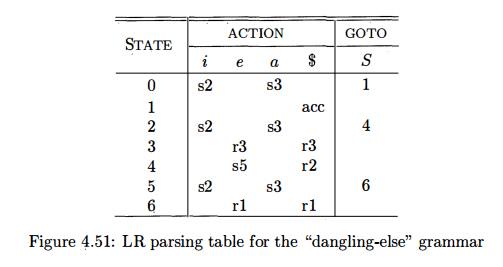
The sets of LR(0) items for grammar (4.67) are shown in Fig. 4.50. The ambi-guity in (4.67) gives rise to a shift/reduce conflict in I4. There, S ->• iS-eS calls for a shift of e and, since F O L L O W ( 5 ) = {e, $}, item S ->• iS- calls for reduction by S -> iS on input e.

Translating back to the if-then-else terminology, given

on the stack and else as the first input symbol, should we shift else onto the stack (i.e., shift e) or reduce if expr t h e n stmt (i.e, reduce by S —> iS)? The answer is that we should shift else, because it is "associated" with the previous then . In the terminology of grammar (4.67), the e on the input, standing for else, can only form part of the body beginning with the iS now on the top of the stack. If what follows e on the input cannot be parsed as an 5, completing body iSeS, then it can be shown that there is no other parse possible.

We conclude that the shift/reduce conflict in J4 should be resolved in favor of shift on input e. The SLR parsing table constructed from the sets of items of Fig. 4.48, using this resolution of the parsing-action conflict in I4 on input e, is shown in Fig. 4.51. Productions 1 through 3 are S -> iSeS, S ->• iS, and S -)• a, respectively.

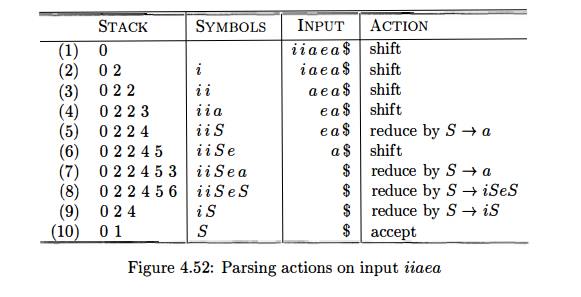
For example, on input iiaea, the parser makes the moves shown in Fig. 4 . 5 2 , corresponding to the correct resolution of the "dangling-else." At line ( 5 ) , state 4 selects the shift action on input e, whereas at line ( 9 ) , state 4 calls for reduction by S ->• iS on input $.

By way of comparison, if we are unable to use an ambiguous grammar to specify conditional statements, then we would have to use a bulkier grammar along the lines of Example 4.16.

3. Error Recovery in LR Parsing

An LR parser will detect an error when it consults the parsing action table and finds an error entry. Errors are never detected by consulting the goto table. An LR parser will announce an error as soon as there is no valid continuation for the portion of the input thus far scanned. A canonical LR parser will not make even a single reduction before announcing an error. SLR and LALR parsers may make several reductions before announcing an error, but they will never shift an erroneous input symbol onto the stack.

In LR parsing, we can implement panic-mode error recovery as follows. We scan down the stack until a state s with a goto on a particular nonterminal A is found. Zero or more input symbols are then discarded until a symbol a is found that can legitimately follow A. The parser then stacks the state GOTO(s, A) and resumes normal parsing. There might be more than one choice for the nonterminal A. Normally these would be nonterminals representing major program pieces, such as an expression, statement, or block. For example, if A is the nonterminal stmt, a might be semicolon or }, which marks the end of a statement sequence.

This method of recovery attempts to eliminate the phrase containing the syntactic error. The parser determines that a string derivable from A contains an error. Part of that string has already been processed, and the result of this processing is a sequence of states on top of the stack. The remainder of the string is still in the input, and the parser attempts to skip over the remainder of this string by looking for a symbol on the input that can legitimately follow

            By removing states from the stack,  skipping over the input,  and pushing GOTO(s, A) on the stack, the parser pretends that it has found an instance of A and resumes normal parsing.

Phrase-level recovery is implemented by examining each error entry in the LR parsing table and deciding on the basis of language usage the most likely programmer error that would give rise to that error. An appropriate recovery procedure can then be constructed; presumably the top of the stack and/or first input symbols would be modified in a way deemed appropriate for each error entry.

In designing specific error-handling routines for an LR parser, we can fill in each blank entry in the action field with a pointer to an error routine that will take the appropriate action selected by the compiler designer. The actions may include insertion or deletion of symbols from the stack or the input or both, or alteration and transposition of input symbols. We must make our choices so that the LR parser will not get into an infinite loop. A safe strategy will assure that at least one input symbol will be removed or shifted eventually, or that the stack will eventually shrink if the end of the input has been reached. Popping a stack state that covers a nonterminal should be avoided, because this modification eliminates from the stack a construct that has already been successfully parsed.

Example 4.68 : Consider again the expression grammar

E -> E + E | E * E | (E) | id

Figure 4.53 shows the LR parsing table from Fig. 4.49 for this grammar, modified for error detection and recovery. We have changed each state that calls for a particular reduction on some input symbols by replacing error entries in that state by the reduction. This change has the effect of postponing the error detection until one or more reductions are made, but the error will still be caught before any shift move takes place. The remaining blank entries from Fig. 4.49 have been replaced by calls to error routines.

The error routines are as follows.

e l : This routine is called from states 0, 2, 4 and 5, all of which expect the beginning of an operand, either an id or a left parenthesis. Instead, +, *, or the end of the input was found.

push state 3 (the goto of states 0, 2, 4 and 5 on id); issue diagnostic "missing operand."

e 2 : Called from states 0, 1, 2, 4 and 5 on finding a right parenthesis.

remove the right parenthesis from the input; issue diagnostic "unbalanced right parenthesis."

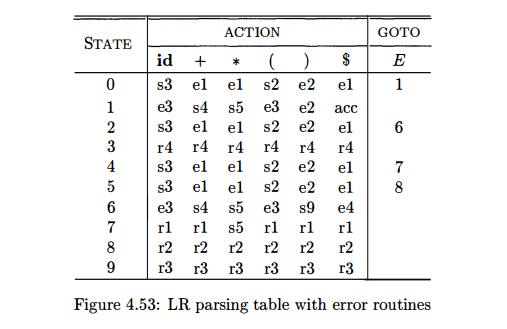
e3: Called from states 1 or 6 when expecting an operator, and an id or right parenthesis is found.

push state 4 (corresponding to symbol +) onto the stack; issue diagnostic "missing operator."

e4:  Called from state 6 when the end of the input is found.

push state 9 (for a right parenthesis) onto the stack; issue diagnostic "missing right parenthesis."

On the erroneous input id + ) , the sequence of configurations entered by the parser is shown in Fig. 4.54. •

4. Exercises for Section 4.8

Exercise 4.8.1 :  The following is an ambiguous grammar for expressions with n binary, infix operators, at n different levels of precedence:

a)  As a function of n, what are the SLR sets of items?

            How would you resolve the conflicts in the SLR items so that all oper-ators are left associative, and 61 takes precedence over 0 ₂ , which takes precedence over # ₃ , and so on?

Show the SLR parsing table that results from your decisions in part (b).

d) Repeat parts (a) and (c) for the unambiguous grammar, which defines the same set of expressions, shown in Fig. 4.55.

How do the counts of the number of sets of items and the sizes of the tables for the two (ambiguous and unambiguous) grammars compare? What does that comparison tell you about the use of ambiguous expression grammars?

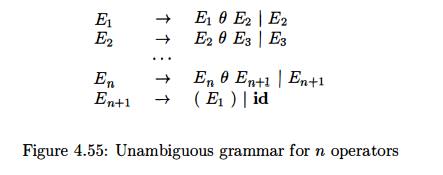
Figure 4.55: Unambiguous grammar for n operators

! Exercise 4 . 8 . 2 : In Fig. 4.56 is a grammar for certain statements, similar to that discussed in Exercise 4.4.12. Again, e and s are terminals standing for conditional expressions and "other statements," respectively.

 Build an LR parsing table for this grammar, resolving conflicts in the usual way for the dangling-else problem.

 Implement error correction by filling in the blank entries in the parsing table with extra reduce-actions or suitable error-recovery routines.

 Show the behavior of your parser on the following inputs:

(i) if e then s ; if e then s end

(ii) while e do begin s ; if e then s ; end