Volume of sphere/hemisphere

1. Volume of sphere

Let r be the radius of a sphere then its volume is given by V = 4/3  πr³ cu. units.

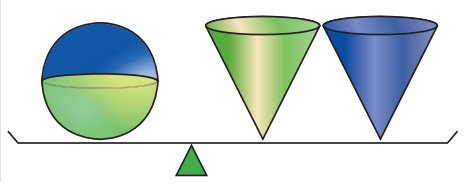
Demonstration

·        Consider a sphere and two right circular cones of same base radius and height such that twice the radius of the sphere is equal to the height of the cones.

·        Then we can observe that the contents of two cones will exactly occupy the sphere.

From the Fig.7.30, we see that

Volume of a sphere  = 2 × (Volume of a cone)

where the diameters of sphere and cone are equal to the height of the cone.

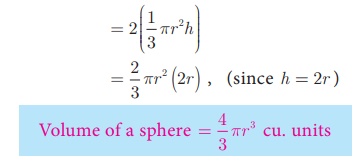
Volume of a sphere = 4/3 πr³ cu. Units

2. Volume of a hollow sphere / spherical shell (volume of the material used)

Let r and R be the inner and outer radius of the hollow sphere. Volume enclosed between the outer and inner spheres

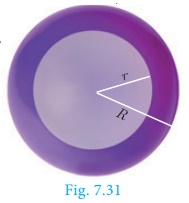
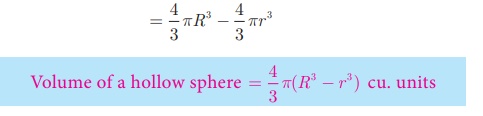
Volume of a hollow sphere = 4/3 π(R³ − r³ ) cu. Units

3. Volume of solid hemisphere

Let r be the radius of the solid hemisphere.

Volume of the solid hemisphere = ½ (volume of sphere)

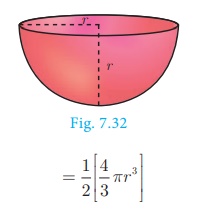
Volume of a solid hemisphere = 2/3 πr³ cu. Units

4. Volume of hollow hemisphere (volume of the material used)

Let r and R be the inner and outer radius of the hollow hemisphere.

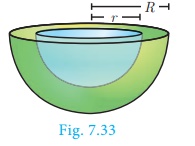
Volume of a hollow hemisphere = 2/3 π(R³ − r³ ) cu. Units

Example 7.21 The volume of a solid hemisphere is 29106 cm³. Another hemisphere whose volume is two-third of the above is carved out. Find the radius of the new hemisphere.

Solution  Let r be the radius of the hemisphere.

Given that, volume of the hemisphere = 29106 cm³

Now, volume of new hemisphere = 2/3 (Volume of original sphere)

=  2/3 × 29106

Volume of new hemisphere = 19404 cm³

2/3 πr ³   = 19404

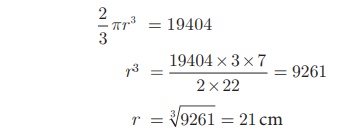
Therefore,  r = 21 cm

Example 7.22 Calculate the weight of a hollow brass sphere if the inner diameter is 14 cm and thickness is 1mm, and whose density is 17.3 g/ cm³.

Solution  Let r and R be the inner and outer radii of the hollow sphere.

Given that, inner diameter d = 14 cm; inner radius r = 7 cm; thickness = 1 mm = 1/10 cm

Outer radius R = 7 + 1/10 = 71/10 = 7.1 cm

But, weight of brass in 1 cm³  = 17.3 gm

Total weight = 17.3×62.48 = 1080.90 gm

Therefore, total weight is 1080.90 grams.