Definition, Formula, Solved Example Problems | Mensuration | Mathematics - Volume of frustum of a cone | 10th Mathematics : UNIT 7 : Mensuration
Chapter: 10th Mathematics : UNIT 7 : Mensuration
Volume of frustum of a cone
Volume of frustum of a cone
Let H and h be the height of cone and frustum respectively, L and l be the slant height of the same.
If
R, r are the radii of the circular bases of the frustum, then volume of the frustum of the cone is the difference
of the volumes of the two cones.
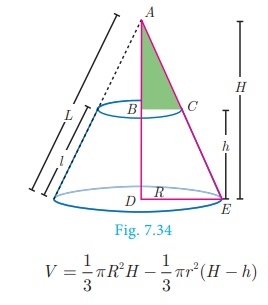
Since
the triangles ABC and ADE are similar, the ratio of their corresponding sides
are proportional.

Example 7.23 If the radii of the circular ends of
a frustum which is 45 cm high are 28 cm and 7 cm, find the volume of the
frustum.
Solution :
Let
h, r and R be the height, top and bottom radii of the frustum.
Given
that, h = 45 cm, R = 28 cm, r = 7 cm

Therefore,
volume of the frustum is 48510 cm3
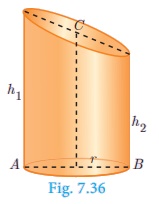
The adjacent figure represents an oblique frustum of a cylinder.
Suppose this solid is cut by a plane through C, not parallel to the base AB,
then
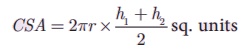
where h1 and
h2 denote the greatest and
least height of the frustum.
Then its volume = 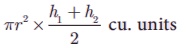
Related Topics