Surface Area: Right Circular Cylinder

Surface Area

Surface area is the measurement of all exposed area of a solid object.

Right Circular Cylinder

Observe the given figures in Fig.7.2 and identify the shape. 

These objects resemble the shape of a cylinder.

Definition : 

A right circular cylinder is a solid generated by the revolution of a rectangle about one of its sides as axis.

If the axis is perpendicular to the radius then the cylinder is called a right circular cylinder. In the Fig.7.3, AB = h represent the height and AD = r represent the radius of the cylinder.

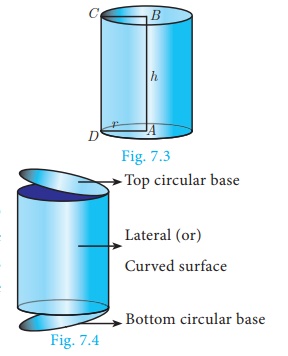
A solid cylinder is an object bounded by two circular plane surfaces and a curved surface.  The area between the two circular bases is called its ‘Lateral Surface Area’ (L.S.A.) or ‘Curved Surface Area’ (C.S.A.).

Formation of a Right Circular Cylinder – Demonstration

(i) Take a rectangle sheet of a paper of length l and breadth b.

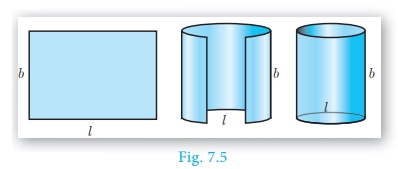
(ii) Revolve the paper about one of its sides, say b to complete a full rotation (without overlapping). 

(iii) The  shape  thus formed will  be a  right  circular cylinder whose circumference of the base is l and the height is b.

Surface Area of a Right Circular Cylinder

(i) Curved surface area

Curved surface area (C.S.A.) of a right circular cylinder

 = Area of the corresponding rectangle

 = l ×b

 = 2πr ×h (since, l is the circumference of the base, b is the height)[see Fig. 7.5]

 = 2πrh

C.S.A. of a right circular cylinder = 2πrh sq. units.

(ii) Total surface area

Total surface area refers to the sum of areas of the curved surface area and the two circular regions at the top and bottom.

That is, total surface area (T.S.A.) of right circular cylinder

= C.S.A + Area of top circular region +Area of bottom circular region.

 = 2πrh + πr ² + πr ²   (Refer Fig.7.4)

= 2πrh + 2πr ²

= 2πr (h + r )

T.S.A. of a right circular cylinder = 2πr (h + r) sq. units

Note

We always consider π = 22/7 , unless otherwise stated.

The term ‘surface area’ refers to ‘total surface area’.

Example 7.1

A cylindrical drum has a height of 20 cm and base radius of 14 cm. Find its curved surface area and the total surface area.

Solution

Given that, height of the cylinder h = 20 cm ; radius r =14 cm

Now, C.S.A. of the cylinder = 2πrh sq. units

C.S.A. of the cylinder  = 2 × (22/7) × 14 ×20 = 2 ×22 × 2 ×20 = 1760 cm²

T.S.A. of the cylinder  = 2πr (h+ r) sq. units

 = 2 × (22/7) × 14 ×(20 + 14) = 2 × 22/7 × 14 ×34

= 2992 cm²

Therefore, C.S.A. = 1760 cm² and T.S.A. = 2992 cm²

Example 7.2

The curved surface area of a right circular cylinder of height 14 cm is 88 cm² . Find the diameter of the cylinder.

Solution

Given that, C.S.A. of the cylinder =88 sq. cm

2πrh =88

2 × (22/7) × r ×14 =88    (given h=14 cm)

2r = (88×7) / (22×14) = 2

Therefore, diameter = 2 cm

Example 7.3

A garden roller whose length is 3 m long and whose diameter is 2.8 m is rolled to level a garden. How much area will it cover in 8 revolutions?

Solution

Given that, diameter d = 2.8 m and height = 3 m

radius r = 1.4 m

Area covered in one revolution = curved surface area of the cylinder

= 2πrh sq. units

= 2 × (22/7) × 1.4 ×3 = 26.4

Area covered in 1 revolution = 26.4 m²

Area covered in 8 revolutions = 8 ×26.4 = 211.2

Therefore, area covered is 211.2 m²

Thinking Corner

1. When ‘h’ coins each of radius ‘r’ units and thickness 1 unit is stacked one upon the other, what would be the solid object you get? Also find its C.S.A.

2. When the radius of a cylinder is double its height, find the relation between its C.S.A. and base area.

3. Two circular cylinders are formed by rolling two rectangular aluminum sheets each of dimensions 12 m length and 5 m breadth, one by rolling along its length and the other along its width. Find the ratio of their curved surface areas.