Volume of a hollow cylinder (volume of the material used)

Volume of a hollow cylinder (volume of the material used)

Let the internal and external radii of a hollow cylinder be r and R units respectively. If the height of the cylinder is h units then

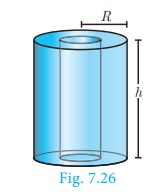
V = πR ²h − πr²h = π(R ² −r² )h

Volume of a hollow cylinder = π(R ² −r² )h cu. units.

Example 7.15

Find the volume of a cylinder whose height is 2 m and whose base area is 250 m².

Solution

Let r and h be the radius and height of the cylinder respectively.

Given that, height h = 2 m, base area = 250 m²

Now, volume of a cylinder = πr²h cu. Units

= base area × h

= 250×2 = 500  m³

Therefore,  volume of the cylinder = 500  m³

Example 7.16

The volume of a cylindrical water tank is 1.078 × 10⁶ litres. If the diameter of the tank is 7 m, find its height.

Solution

Let r and h be the radius and height of the cylinder respectively.

Given that, volume of the tank = 1.078 ×10⁶ = 1078000 litre

= 1078 m³

= 1078 m³ (since 1l = 1/1000 m³)

 diameter = 7m gives radius = 7/2 m

volume of the tank = πr²h cu. Units

1078  = 22/7 × 7/2 × 7/2 ×h

Therefore, height of the tank is 28 m

Example 7.17

Find the volume of the iron used to make a hollow cylinder of height 9 cm and whose internal and external radii are 21 cm and 28 cm respectively.

Solution Let r, R and h be the internal radius, external radius and height of the hollow cylinder respectively.

Given that, r =21cm, R = 28 cm, h = 9 cm

Now, volume of hollow cylinder = π(R² −r² )h cu. Units

= 22/7 (28² − 21² )×9

= 22/7 (784 − 441) ×9 = 9702

Therefore, volume of iron used = 9702 cm³

Example 7.18

For the cylinders A and B (Fig. 7.27),

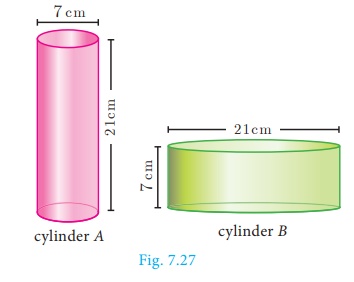
(i) find out the cylinder whose volume is greater.

(ii) verify whether the cylinder with greater volume has greater total surface area.

(iii) find the ratios of the volumes of the cylinders A and B.

Solution

(i) Volume of cylinder = πr²h cu. Units

Volume of cylinder A = 22/7 × 7/2 × 7/2 ×21

= 808. 5 cm³

Volume of cylinder B = 22/7 × 21/2 × 21/2 × 7

= 2425. 5 cm³

Therefore, volume of cylinder B is greater than volume of cylinder A.

(ii) T.S.A. of cylinder = 2πr (h + r) sq. units

T.S.A. of cylinder A = 2 × (22/7) × (7/2) ×(21 + 3. 5) = 539 cm²

T.S.A. of cylinder B = 2 × (22/7) × (21/2) ×(7 + 10. 5) = 1155 cm²

Hence verified that cylinder B with greater volume has a greater surface area.

(iii)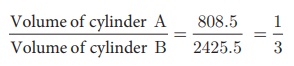 

Therefore, ratio of the volumes of cylinders A and B is 1:3.