Conversion of Solids from one shape to another with no change in Volume

Conversion of Solids from one shape to another with no change in Volume

Conversions or Transformations becomes a common part of our daily life. For example, a gold smith melts a bar of gold to transform it to a jewel. Similarly, a kid playing with clay shapes it into different toys, a carpenter uses the wooden logs to form different house hold articles/furniture. Likewise, the conversion of solids from one shape to another is required for various purposes.

In this section we will be learning problems involving conversions of solids from one shape to another with no change in volume.

Example 7.29 A metallic sphere of radius 16 cm is melted and recast into small spheres each of radius 2 cm. How many small spheres can be obtained?

Solution  Let the number of small spheres obtained be n.

Let r be the radius of each small sphere and R be the radius of metallic sphere.

Here, R = 16 cm, r = 2 cm

Now, n×(Volume of a small sphere) = Volume of big metallic sphere

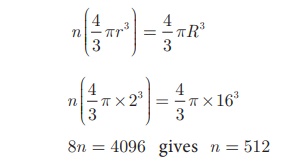
8n = 4096 gives n = 512

Therefore, there will be 512 small spheres.

Example 7.30

A cone of height 24 cm is made up of modeling clay. A child reshapes it in the form of a cylinder of same radius as cone. Find the height of the cylinder.

Solution  Let h₁  and h₂  be the heights of a cone and cylinder respectively.

Also, let r be the raius of the cone.

Given that, height of the cone h₁ = 24 cm; radius of the cone and cylinder r = 6 cm

Since, Volume of cylinder = Volume of cone

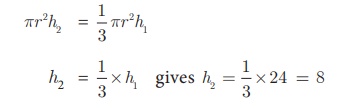
Therefore, height of cylinder is 8 cm

Example 7.31 A right circular cylindrical container of base radius 6 cm and height 15 cm is full of ice cream. The ice cream is to be filled in cones of height 9 cm and base radius 3 cm, having a hemispherical cap. Find the number of cones needed to empty the container.

Solution  Let h and r be the height and radius of the cylinder respectively.

Given that, h = 15 cm, r = 6 cm

Volume of the container V = πr²h cubic units.

= (22/7) × 6 × 6 ×15

Let, r₁ = 3 cm, h₁ = 9 cm be the radius and height of the cone.

Also, r₁ = 3 cm is the radius of the hemispherical cap.

Volume of one ice cream cone =(Volume of the cone + Volume of the hemispherical cap)

Number of ice cream cones needed = 

Thus 12 ice cream cones are required to empty the cylindrical container.