Surface Area: Frustum of a right circular cone

Frustum of a right circular cone

In olden days a cone shaped buckets [Fig.7.21(a)] filled with sand / water were used to extinguish fire during fire accidents. Later, it was reshaped to a round shaped bottom [Fig.7.21(b)] to increase its volume.

The shape in [Fig.7.21(c)] resembling a inverted bucket is called as a frustrum of a cone.

The objects which we use in our daily life such as glass, bucket, street cone are examples of frustum of a cone. (Fig.7.22)

Definition

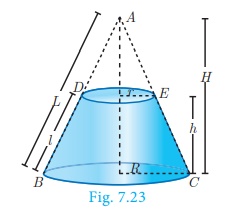
When a cone ABC is cut through by a plane parallel to its base, the portion of the cone DECB between the cutting plane and the base is called a frustum of the cone.

Surface area of a frustum

Let R and r be radii of the base and top region of the frustum DECB respectively, h is the height and l is the slant height of the same.

Therefore, C.S.A. = ½ (sum of the perimeters of base and top region) × slant height 

= ½ (2πR + 2πr)l

C.S.A. of a frustum = π(R + r)l sq. units

Where,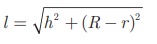 

T.S.A. = C.S.A. + Area of the bottom circular region  + Area of the top circular region.

T.S.A. of a frustum = π(R + r)l + πR²  + πr ²  sq. units

Where,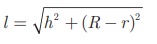 

Example 7.13 The slant height of a frustum of a cone is 5 cm and the radii of its ends are 4 cm and 1 cm. Find its curved surface area.

Solution Let l, R and r be the slant height, top radius and bottom radius of the frustum. 

Given that, l= 5 cm, R = 4 cm, r = 1 cm 

Now,  C.S.A. of the frustum = π (R + r) l sq. units

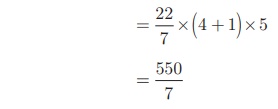
Therefore, C.S.A. = 78.57 cm²

Example 7.14 An industrial metallic bucket is in the shape of the frustum of a right circular cone whose top and bottom diameters are 10 m and 4 m and whose height is 4 m. Find the curved and total surface area of the bucket.

Solution Let h, l, R and r be the height, slant height, outer radius and inner radius of the frustum.

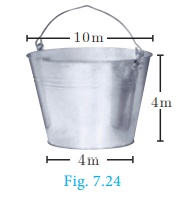
Given that, diameter of the top =10 m; radius of the top R = 5 m.

diameter of the bottom = 4 m; radius of the bottom r = 2 m, height h= 4 m

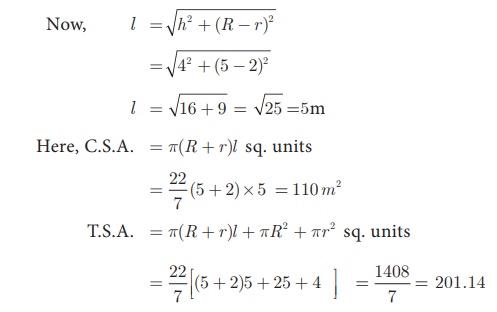
Therefore, C.S.A.  = 110 m² and T.S.A. = 201.14 m²