Surface Area: The Sphere

The Sphere

Definition:

A sphere is a solid generated by the revolution of a semicircle about its diameter as axis.

Every plane section of a sphere is a circle. The line of section of a sphere by a plane passing through the centre of the sphere is called a great circle; all other plane sections are called small circles.

As shown in the diagram, circle with CD as diameter is a great circle, whereas, the circle with QR as diameter is a small circle.

Surface area of a sphere

Archimedes Proof

Place a sphere inside a right circular cylinder of equal diameter and height. Then the height of the cylinder will be the diameter of the sphere. In this case, Archimedes proved that the outer area of the sphere is same as curved surface area of the cylinder.

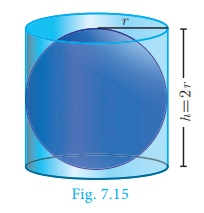
That is, Surface area of sphere =curved surface area of cylinder

 = 2πrh = 2πr (2r)

Surface area of a sphere = 4πr² sq.units

1. Hemisphere

A section of the sphere cut by a plane through any of its great circle is a hemisphere.

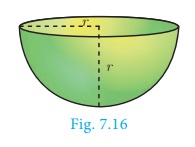
By doing this, we observe that a hemisphere is exactly half the portion of the sphere.

Curved surface area of hemisphere =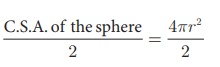 

C.S.A. of a hemisphere = 2πr² sq.units

Total surface area of hemisphere = C.S.A. +Area of top circular region

= 2πr ² +πr²

T.S.A. of a hemisphere = 3πr² sq.units

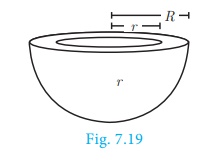
2. Hollow Hemisphere

Let the inner radius be r and outer radius be R, 

then thickness = R−r

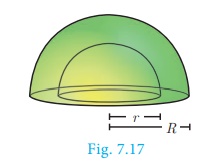
Therefore, C.S.A. = Area of external hemisphere + Area of internal hemisphere

= 2πr² + 2πr²

C.S.A. of a hollow hemisphere = 2π(R²  + r² ) sq. units

T.S.A. = C.S.A. + Area of annulus region

= 2 π (R ²  + r² ) + π (R ² −r² )

= π [2R² + 2r² + R² − r²]

T.S.A. of a hollow hemisphere = π(3R² + r² ) sq. units

Example 7.8

Find the diameter of a sphere whose surface area is 154 m².

Solution

 Let r be the radius of the sphere.

Given that, surface area of sphere = 154 m²

4πr² = 154

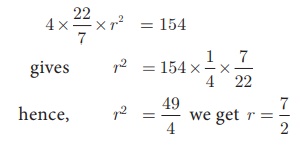
Therefore, diameter is 7 m

Example 7.9

The radius of a spherical balloon increases from 12 cm to 16 cm as air being pumped into it. Find the ratio of the surface area of the balloons in the two cases.

Solution

Let r₁  and r₂ be the radii of the balloons.

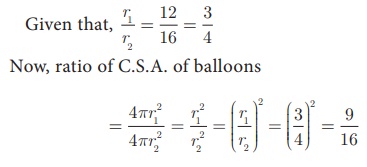
Therefore, ratio of C.S.A. of balloons is 9:16.

Example 7.10

If the base area of a hemispherical solid is 1386 sq. metres, then find its total surface area?

Solution

Let r be the radius of the hemisphere.

Given that, base area = πr²  = 1386 sq. m

T.S.A. = 3πr²  sq.m

 = 3 ×1386  = 4158

Therefore, T.S.A. of the hemispherical solid is 4158 m²  

Note

For finding the C.S.A. and T.S.A. of a hollow sphere, the formulla for finding the surface area of a sphere can be used.

Example 7.11 The internal and external radii of a hollow hemispherical shell are 3 m and 5 m respectively. Find the T.S.A. and C.S.A. of the shell.

Solution Let the internal and external radii of the hemispherical shell be r and R respectively.

Given that, R = 5 m, r =3 m

C.S.A. of the shell = 2π(R²  + r² ) sq. units

= 2 × (22/7) × (25 + 9) = 213.71

T.S.A. of the shell = π (3R²  + r² ) sq. units

= (22/7) × (25 + 9) = 264

Therefore, C.S.A. = 213.71 m²  and T.S.A. = 264 m².

Example 7.12

A sphere, a cylinder and a cone (Fig.7.20) are of the same radius, where as cone and cylinder are of same height. Find the ratio of their curved surface areas.

Solution

Required Ratio = C.S.A. of the sphere: C.S.A. of the cylinder : C.S.A. of the cone

= 4πr²  : 2πrh : πrl ,  (l = √[r ² + h² ] = √[2r²] = √2r units)

= 4 : 2:  √2 = 2√2 :  √2 : 1