Surface Area of Right Circular Cone

Right Circular Cone

Observe the given figures in Fig.7.9 and identify which solid shape they represent?

These objects resemble the shape of a cone.

Definition :

A right circular cone is a solid generated by the revolution of a right angled triangle about one of the sides containing the right angle as axis.

Formation of a Right Circular Cone – Demonstration

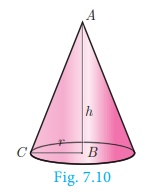
In Fig. 7.10, if the right triangle ABC revolves about AB as axis, the hypotenuse AC generates the curved surface of the cone represented in the diagram. The height of the cone is the length of the axis AB, and the slant height is the length of the hypotenuse AC.

Surface area of a right circular cone

Suppose the surface area of the cone is cut along the hypotenuse AC and then unrolled on a plane, the surface area will take the form of a sector ACD, of which the radius AC and the arc CD are respectively the slant height and the circumference of the base of the cone.

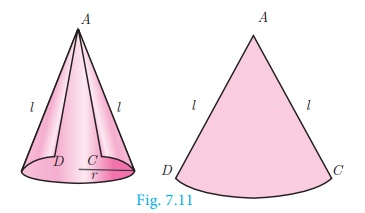
Here the sector of radius ‘l ’ and arc length ‘s’ will be similar to a circle of radius l_.

(i) Curved surface area

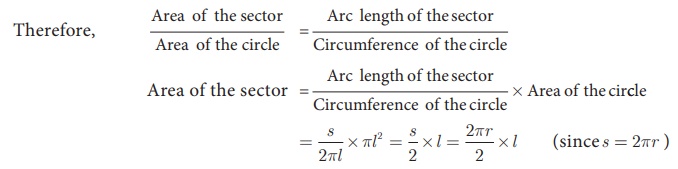
∴ Curved Surface Area of the cone = Area of the Sector = πrl sq. units.

C.S.A. of a right circular cone = πrl sq. units.

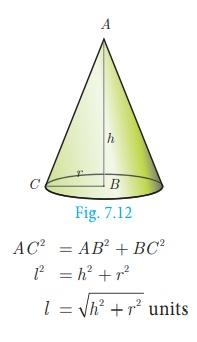
Derivation of slant height ‘l’

ABC is a right angled triangle, right angled at B. The hypotenuse, base and height of the triangle are represented by l, r and h respectively.

Now, using Pythagoras theorem in ΔABC,

(ii) Total surface area

Total surface area of a cone = C.S.A. + base area of the cone

 =  πrl + πr² (since, the base is a circle)

T.S.A. of a right circular cone = πr (l + r ) sq. units.

Example 7.5

The radius of a conical tent is 7 m and the height is 24 m. Calculate the length of the canvas used to make the tent if the width of the rectangular canvas is 4 m? 

Solution

 Let r and h be the radius and height of the cone respectively.

Given that, radius r =7 m and height h = 24 m

Hence, 

C.S.A. of the conical tent = πrl  sq. units

Area of the canvas = (22/7) ×7 ×25 = 550 m²

Now, length of the canvas =  Area of the canvas / width = 550/4 = 137.5 m

Therefore, the length of the canvas is 137.5 m

Example 7.6

If the total surface area of a cone of radius 7cm is 704 cm², then find its slant height.

Solution

Given that, radius r = 7 cm

Now, total surface area of the cone = πr (l + r ) sq. units

T.S.A. = 704 cm²

 704 = (22/7) ×7 (l + 7)

 32 = l + 7  implies l = 25 cm

Therefore, slant height of the cone is 25 cm.

Example 7.7

From a solid cylinder whose height is 2.4 cm and diameter 1.4 cm, a conical cavity of the same height and base is hollowed out (Fig.7.13). Find the total surface area of the remaining solid.

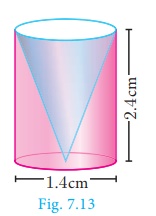
Solution

 Let h and r be the height and radius of the cone and cylinder.

Let l be the slant height of the cone.

Given that, h = 2.4 cm and d = 1.4 cm ; r = 0.7 cm

1= 2.5 cm

Area of the remaining solid = 2πrh + πrl + πr²  sq. units

= πr (2h + l + r )

= (22/7) × 0.7 × [(2 × 2.4) + 2.5 + 0.7]

= 17.6

Therefore, total surface area of the remaining solid is 17.6 m²