Applications of Integration | Mathematics - Volume of a solid obtained by revolving area about an axis | 12th Maths : UNIT 9 : Applications of Integration
Chapter: 12th Maths : UNIT 9 : Applications of Integration
Volume of a solid obtained by revolving area about an axis
Volume of a solid obtained by revolving area about an axis
Definite integrals have applications in finding volumes of solids of revolution about a fixed axis. By a solid of revolution about a fixed axis, we mean that a solid is generated when a plane region in a given plane undergoes one full revolution about a fixed axis in the plane. For instance, consider the semi circular plane region inside the circle x2 + y2 = a2 and above the x-axis. See Fig.9.34.
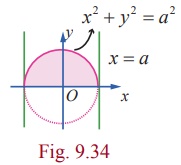
If this region is given one complete rotation (revolution for 360┬░ = 2ŽĆ radians) about x-axis, then a solid called a sphere is generated.

In the same manner, if you want to generate a right-circular cylinder with radius a and height h, you can consider the rectangular plane region bounded between the straight lines y = 0 , y = a , x = 0 and x = h in the xy-plane. See Fig.9.35. If this region is given one complete rotation (revolution for 360┬░ = 2ŽĆ radians) about x-axis, then a solid called a cylinder is generated.
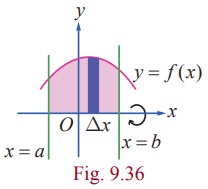
We restrict ourselves to obtain volume of solid of revolution about x-axis or y-axis. Whenever solid of revolution about x-axis is considered, the plane region that is revolved about x-axis lies above the x-axis. So, in this region y Ōēź 0 . Whenever solid of revolution about y-axis is considered, the plane region that is revolved about y-axis lies to the right of y-axis. So, in this region x Ōēź 0 . We shall find the formula for finding the volume of the solid of revolution of the plane region in the first quadrant bounded by the curve y = f ( x) , x-axis and the lines x = a and x = b > a about x-axis. The derivation of the formula is based upon the formula that the volume of a cylinder of radius r and the height is ŽĆr 2 h .
Assume that every line parallel to y-axis lying between the lines x = a and x = b > a cuts the curve y = f ( x) in the first quadrant exactly at one point. Divide [ a,b] into n segments by x1 , x2 ,. . ., xnŌłÆ1 such that

For each i = 0,1, 2,..., n ŌłÆ1 , the region in the xy-plane between the ordinates at xi and xi + ╬öx which lies between the x-axis and the curve y = f ( x) can be approximated to an infinitesimal rectangle having area yi╬öx , where yi = f ( xi ) . When the plane region bounded by the curve y = f ( x) , x-axis, and lines x = a and x = b is rotated by 360┬║ about x-axis, each of the infinitesimal rectangles at x = xi also revolves and generates an elementary solid which is approximately a thin cylindrical disc with radius yi and height ╬öx . See Fig.9.36. The volume of the cylindrical disc at x = xi is given by ŽĆ yi2╬öx , i = 0,1, 2,. . ., n ŌłÆ1 . Summing all these elementary volumes, we get the approximate volume of the solid of revolution as 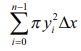 . Let n become larger and larger ( n ŌåÆ Ōł×) such that ╬öx becomes smaller and smaller (╬öx ŌåÆ 0) . Then
. Let n become larger and larger ( n ŌåÆ Ōł×) such that ╬öx becomes smaller and smaller (╬öx ŌåÆ 0) . Then 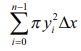 tends to the volume of the solid of revolution. Hence the volume of the solid of revolution is aŌł½b y2dx.
tends to the volume of the solid of revolution. Hence the volume of the solid of revolution is aŌł½b y2dx.
Similarly, we can find the formula for finding the volume of the solid of revolution of the region bounded by the curve x = f ( y ) , y-axis, and the lines y = c and y = d about y-axis. The curve x = f ( y ) lies to the right of y-axis between the lines y = c and y = d > c . Assume that every line parallel to x-axis between y = c and y = d > c cuts the curve x = f ( y ) in the first quadrant exactly at one point. See Fig.9.37. Then, the volume of the solid of revolution is given by ŽĆŌł½cdx2dy.
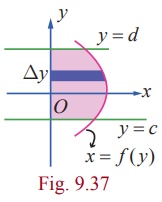
Example 9.62
Find the volume of a sphere of radius a.
Solution
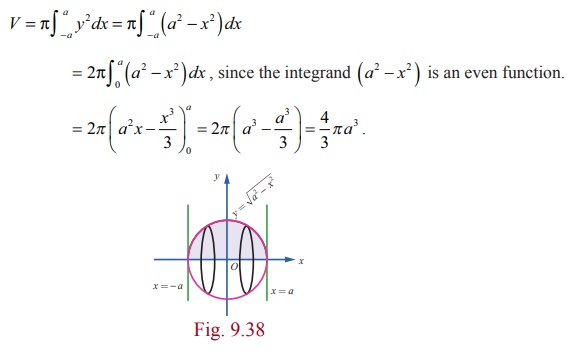
By revolving the upper semicircular region enclosed between the circle x2 + y2 = a2 and the x-axis, we get a sphere of radius a. See Fig. 9.38.
The boundaries of the region are y = ŌłÜ[a2 ŌłÆ x2], x-axis, the lines x = ŌłÆa and x = a . Hence, the volume of the sphere is given by
Example 9.63
Find the volume of a right-circular cone of base radius r and height h.
Solution
Consider the triangular region in the first quadrant which is bounded by the line y = r/h x , x-axis, the lines x = 0 and x = h . See Fig.9.39. By revolving the region about the x-axis, we get a cone of base radius r and height h.
Hence, the volume of the cone is given by

Example 9.64
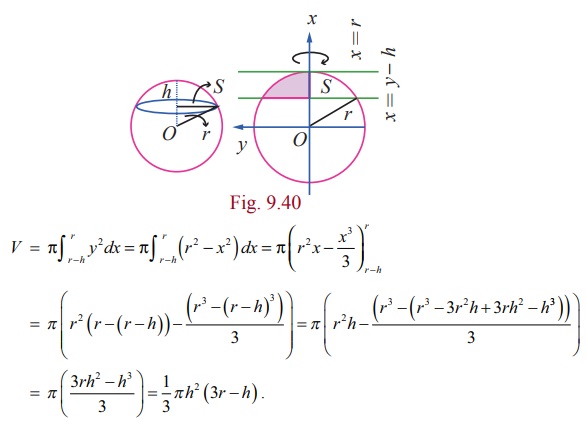
Find the volume of the spherical cap of height h cut of from a sphere of radius r.
Solution
If the region in the first quadrant bounded by the circle x2 + y2 = r 2 , the x-axis, the lines x = r ŌłÆ h and x = r is revolved about the x-axis, then the solid generated is a spherical cap of height h cut of from a sphere of radius r. See Fig. 9.40. Hence, the required volume is given by
Note
We can rewrite the above volume in terms of the radius of the cap.
If Žü is the radius of the cap, then Žü 2 + ( r ŌłÆ h)2 = r2 .
Then, we have
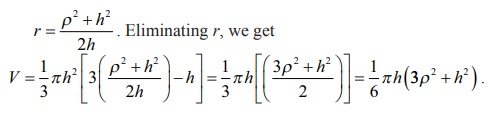
Example 9.65
Find the volume of the solid formed by revolving the region bounded by the parabola y = x2 , x-axis, ordinates x = 0 and x = 1 about the x-axis.
Solution
The region to be revolved about the x-axis is sketched as in Fig.9.41. Hence, the required volume is given by
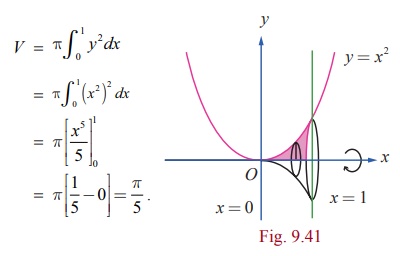
Example 9.66
Find the volume of the solid formed by revolving the region bounded by the ellipse  about the major axis.
about the major axis.
Solution
The ellipse is symmetric about both the axes. The major axis lies along x-axis. The region to be revolved is sketched as in Fig.9.42.
Hence, the required volume is given by

Note
If the region bounded by ellipse  = 1 is revolved about the y-axis, then the volume of the solid of revolution is 4ŽĆa2b / 3 . The solid is called an ellipsoid.
= 1 is revolved about the y-axis, then the volume of the solid of revolution is 4ŽĆa2b / 3 . The solid is called an ellipsoid.
Example 9.67
Find, by integration, the volume of the solid generated by revolving about y-axis the region bounded between the parabola x = y2 +1, the y-axis, and the lines y = 1 and y = ŌłÆ1.
Solution
The parabola x = y2 +1 is y2= x ŌłÆ1. It is symmetrical about x-axis and has the vertex at (1, 0) and focus at (5/4, 0). The region for revolution is shaded in Fig.9.43. Hence, the required volume is given by
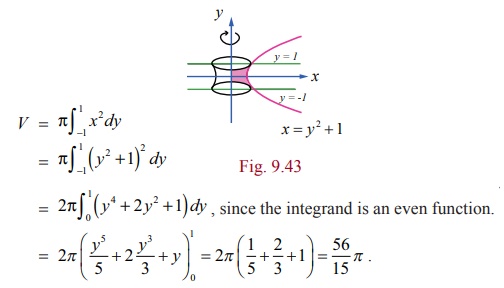
Example 9.68
Find, by integration, the volume of the solid generated by revolving about y-axis the region bounded between the curve y = 3/4 ŌłÜ[x2 ŌłÆ16] , x Ōēź 4 , the y-axis, and the lines y = 1 and y = 6.
Solution
We note that y = 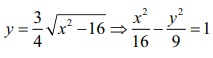 . So, the given curve is a portion of the hyperbola
. So, the given curve is a portion of the hyperbola 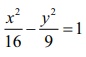 between the lines y =1 and y = 6 and it lies above the x-axis.
between the lines y =1 and y = 6 and it lies above the x-axis.
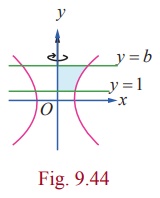
The region to be revolved is sketched in Fig.9.44.
Since revolution is made about y-axis, we write the equation of the portion of the hyperbola as x = 4/3 ŌłÜ[9+y2]. So, the volume of the solid generated is given by

Example 9.69
Find, by integration, the volume of the solid generated by revolving about y-axis the region bounded by the curves y = log x , y = 0 , x = 0 and y = 2 .
Solution
The region to be revolved is sketched in Fig.9.45.
Since revolution is made about the y-axis, the volume of the solid generated is given by
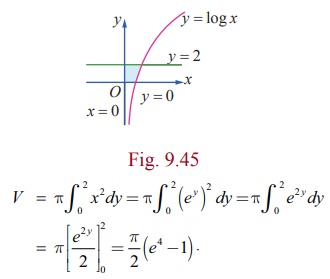
Related Topics