Applications of Integration - BernoulliŌĆÖs Formula | 12th Maths : UNIT 9 : Applications of Integration
Chapter: 12th Maths : UNIT 9 : Applications of Integration
BernoulliŌĆÖs Formula
BernoulliŌĆÖs
Formula
The
evaluation of an indefinite integral of the form Ōł½u (x) v
( x)dx becomes very simple, when u
is a polynomial function of x
(that is, u ( x) = a0
xn +
a1 xnŌłÆ1 + + an )
and v ( x) can be easily integrated successively. It is accomplished by a
formula called BernoulliŌĆÖs
formula. This formula is actually an extension of the formula of
integration by parts. To derive the formula, we use the following notation:

Proceeding
in this way, we get
Ōł½ uvdx = uv(1) ŌłÆ u (1)v( 2) + u ( 2)v( 3) ŌłÆ u (3)v( 4) + .
The
above result is called the BernoulliŌĆÖs formula for integration of product of two
functions.
Note
Since u is a polynomial function of x , the successive derivative u( m)
will be zero for some positive integer m
and so all further derivatives will be zero only. Hence the right-hand-side of
the above formula contains a finite number of terms only.
Example 9.31
Evaluate
ŽĆŌł½0 x2
cos nx dx , where n is a positive integer.
Solution
Taking u = x2
and v = cos nx , and applying the BernoulliŌĆÖs formula, we get
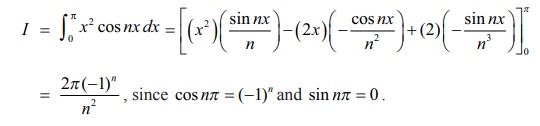
Example 9.32
Evaluate
: 1Ōł½0 eŌłÆ2x (1 + x
ŌłÆ
2x3 ) dx .
Solution
Taking u = 1 + x
ŌłÆ
2x3 and v = eŌłÆ2x , and applying the BernoulliŌĆÖs formula, we get
I = 1Ōł½0 eŌłÆ2x (1+ x
ŌłÆ
2x3 ) dx
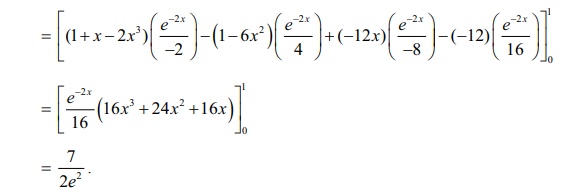
Example 9.33
Evaluate
: 2ŽĆŌł½0 x2
sin nx dx , where n is a positive integer.
Solution
Taking u = x2
and v = sin nx , and applying the BernoulliŌĆÖs formula, we get
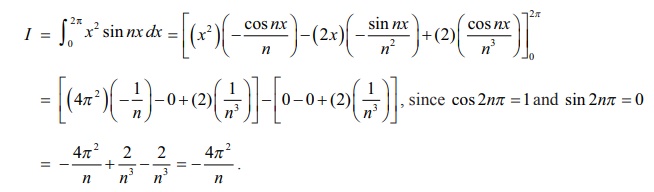
Example 9.34
Evaluate
: 1Ōł½ŌłÆ1 eŌłÆ ╬╗x (1 ŌłÆ x2
) dx .
Solution
Taking u = 1ŌłÆ x2
and v = eŌłÆ╬╗ x
, and applying the BernoulliŌĆÖs formula, we get
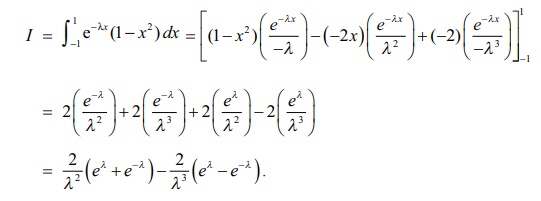
Related Topics