Applications of Integration | Mathematics - Evaluation of a Bounded Plane Area by Integration | 12th Maths : UNIT 9 : Applications of Integration
Chapter: 12th Maths : UNIT 9 : Applications of Integration
Evaluation of a Bounded Plane Area by Integration
Evaluation of a
Bounded Plane Area by Integration
In the
beginning of this chapter, we have already introduced definite integral by a
geometrical approach. In that approach, we have noted that, whenever the
integrand of the definite integral is non-negative, the definite integral
yields the geometrical area. In the present section, we apply the approach for
finding areas of plane regions bounded by plane curves.
1. Area of the region
bounded by a curve, x
ŌĆō axis and the lines x = a and x = b.
Case
(i)
Let y = f
( x ), a Ōēż x Ōēż
b be the equation of the portion of
the continuous curve that lies above the x
ŌłÆ axis (that is, the portion lies either in the first quadrant
or in the second quadrant) between the lines x = a and x = b
. See Fig.9.8. Then, y Ōēź
0 for every point of the portion of the curve. Consider the region bounded by
the curve, x ŌłÆ axis, the ordinates x = a and x = b . It is important to note that y does not change its sign in the
region. Then, the area A of the
region is found as follows:
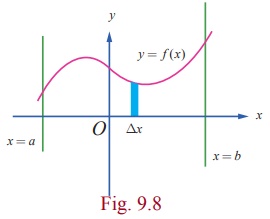
Viewing
in the positive direction of the y ŌłÆ
axis, divide the region into elementary vertical strips (thin rectangles) of
height y and width Δx . Then, A is the limit sum of the areas of the
vertical strips.
Hence,
we get

Case
(ii)
Let y = f
( x ), a Ōēż x Ōēż
b be the equation of the portion of the
continuous curve that lies below the x
ŌłÆ
axis (that is, the portion lies either
in the third quadrant or in the fourth quadrant).
Then, y Ōēż
0 for every point of the portion of the curve. It is important to note that y does not change its sign in the region. Consider the region bounded by the curve,
x
ŌłÆ axis, the ordinates x = a and x = b . See Fig.9.9. Then, the area
A of the region is found as follows:
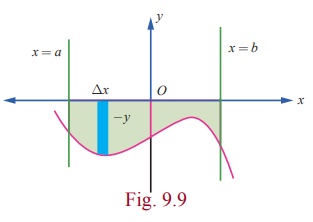
Viewing
in the negative direction of the y ŌłÆ
axis, divide the region into elementary vertical strips (thin rectangles) of
height |y| = ŌłÆ y and width ╬öx . Then, A is the limit of the sum of the areas
of the vertical strips. Hence, we get
A = lim ŌłæaŌēżxŌēżb
ŌłÆy╬öx = ŌłÆbŌł½a ydx = | bŌł½a ydx | .
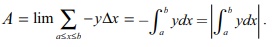
Case
(iii)
Let y = f
( x ), a Ōēż x Ōēż
b be the equation of the portion of
the continuous curve that lies above as well as below the x ŌłÆ axis (that is, the portion may lie in all quadrants).
Draw the
graph of y = f (
x) in the XY ŌłÆ plane. The graph lies alternately above
and below the x ŌłÆ
axis and it is intercepted between the ordinates x = a and x = b.
Divide
the interval[a , b] into subintervals [a ,
c1 ] , [c1 , c2 ] , . . . , [ck
, b] such that f ( x) has the same sign
on each of subintervals. Applying cases (i) and (ii), we can obtain individually,
the geometrical areas of the regions corresponding to the subintervals.
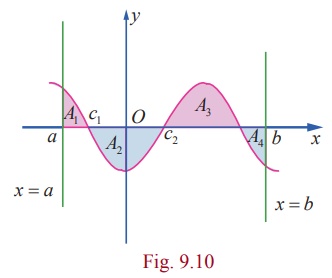
Hence
the geometrical area of the region bounded by the graph of y = f ( x) , the x-axis, the lines x = a and x = b is given by
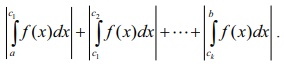
For
instance, consider the shaded region in Fig. 9.10. Here A1 , A2
, A3 , and A4 denote geometric areas
of the individual parts. Then, the total area is given by
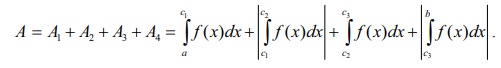
2. Area of the region bounded by a curve, yŌĆō axis and the lines y = c and y = d.
Case
(iv)
Let x = f
( y ), c Ōēż y Ōēż
d be the equation of the portion of the
continuous curve that lies to the right side of y
ŌłÆ axis (that is, the portion lies either in the first quadrant
or in the fourth quadrant). Then, x Ōēź 0 for every point of the portion of the curve. It is
important to note that x does not
change its sign in the region.

Consider
the region bounded by the curve, y ŌłÆ axis, the lines y = c and y = d . The region is sketched as in Fig.
9.11. Then, the area A of the region
is found as follows:
Viewing in the positive direction of the x ŌłÆ axis, divide the region into thin horizontal strips (thin rectangles) of length x and width ╬öy . Then, A is the limit of the sum of the areas of the horizontal strips. Hence, we get A = lim ŌłæcŌēżyŌēżd x╬ö y = dŌł½c xdy.
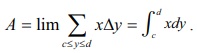
Case
(v)
Let x = f
( y ), c Ōēż y Ōēż
d be the equation of the portion of the
continuous curve that lies to the left side of y ŌłÆ axis (that is, the portion lies either in the second
quadrant or in the third quadrant). Then, x
Ōēż
0 for every point of the portion of the curve. It is important to note that x does not change its sign in the region. Consider the region bounded by
the curve, y ŌłÆ axis, the lines y = c and y = d . The region is sketched as in Fig.
9.12. Then, the area A of the region
is found as follows:
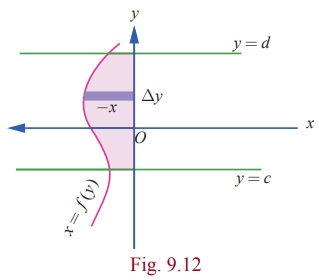
Viewing
in the positive direction of the x ŌłÆ
axis, divide the region into thin horizontal strips (thin rectangles) of length
|x| = ŌłÆx and width ╬öy . Then, A is the limit of the sum of the areas
of the horizontal strips.
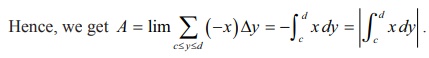
Case
(vi)
Let x = f
( y ), c Ōēż y Ōēż
d be the equation of the portion of
the continuous curve that lies to the right as well as to the left of the y ŌłÆ axis (that is, the portion may lie
in all quadrants). Draw the graph of x
=
f ( y) in the XY ŌłÆ
plane. The graph lies alternately to the right and to the left of the y ŌłÆ axis and it is intercepted between
the lines y =
c and y = d . Divide the
interval [c , d ] into subintervals [c
, a1 ] , [a1 , a2 ] , . . . , [ak
, d ] such that f ( y) has the same sign
on each of subintervals. Applying cases (iii) and (iv), we can obtain
individually, the geometrical areas of the regions corresponding to the subintervals.

Hence the
geometrical area A of the region bounded by the graph of x = f ( y) , the y-axis,
the lines y = c and y = d
is given by
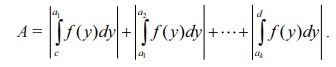
For
instance, consider the shaded region in Fig. 9.13. Here, B1 , B2
, B3
and B4 denote geometric
areas of the individual parts. Then the
total area B
of the region bounded by the curve
x = f(y), y ŌłÆ axis and the lines y = c and y = d
is given by
B = B1+B2+B3+B4

Example 9.47
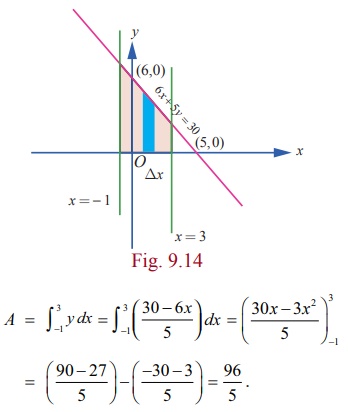
Find the
area of the region bounded by the line 6x
+
5y = 30 , x ŌłÆ axis and the lines x
= ŌłÆ1
and x = 3 .
Solution
The
region is sketched in Fig. 9.14. It lies above the x ŌłÆ axis. Hence, the required area is given by
Example 9.48
Find the
area of the region bounded by the line 7x
ŌłÆ
5y = 35 , x ŌłÆ axis and the lines x
= ŌłÆ2
and x = 3.
Solution
The
region is sketched in Fig. 9.15. It lies below the x ŌłÆ axis. Hence, the required area is given by

Example 9.49
Find the
area of the region bounded by the ellipse
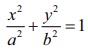
Solution
The
ellipse is symmetric about both major and minor axes. It is sketched as in
Fig.9.16. So, viewing in the positive direction of y -axis, the required area A is
four times the area of the region bounded by the portion of the ellipse in the
first quadrant

Note
Viewing
in the positive direction of x -axis,
the required y area A is four times the area of the region
bounded by the portion of the ellipse in the first quadrant
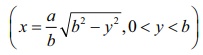
y-axis,
y = 0 and y = b. Hence, by taking horizontal strips (see Fig.9.17), we get
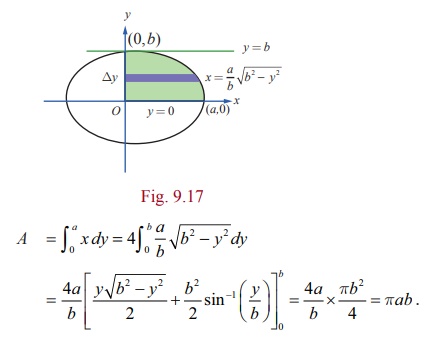
Note
Putting b = a
in the above result, we get that the area of the region enclosed by the circle x2+ y2 = a2 is ŽĆa2 .
Example 9.50
Find the
area of the region bounded between the parabola y2 = 4ax and its
latus rectum.
Solution
The equation of the latus-rectum is x = a . It intersects the parabola at the points L ( a, 2a) and L1 ( a, ŌłÆ2a) . The required area is sketched in Fig. 9.18. By symmetry, the required area A is twice the area bounded by the portion of the parabola
y = 2 ŌłÜaŌłÜx ,
x -axis, x = 0 and x = a.
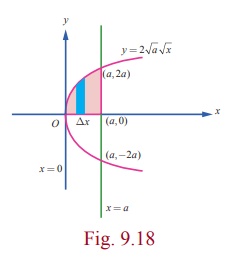
Hence,
by taking vertical strips, we get
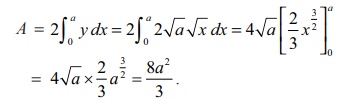
Note
Viewing
in the positive direction of x-axis,
and making horizontal strips (see Fig. 9.19), we get

Note
It is
quite interesting to note that the above area is equal to two-thirds the base
(latus-rectum) times the height (the distance between the focus and the
vertex). This verifies ArchimedesŌĆÖ formula for areas of parabolic arches which
states that the area under a parabolic arch is two-thirds the area of the
rectangle having base of the arch as length and height of the arch as the breadth.
It is also equal to four-thirds the area of the triangle with base
(latus-rectum) and height (the distance between the focus and the vertex).
Example 9.51
Find the
area of the region bounded by the y
-axis and the parabola x =
5 ŌłÆ
4 y ŌłÆ y2.
Solution
The
equation of the parabola is ( y +
2)2 = ŌłÆ ( x ŌłÆ 9) . The parabola crosses the y -axis at (0, ŌłÆ5) and (0,1) .The vertex is at (9, ŌłÆ2)
and the axis of the parabola is y = ŌłÆ2
. The required area is sketched as in Fig. 9.20.
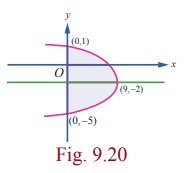
Viewing
in the positive direction of x ŌłÆ
axis, and making horizontal strips, the required area A is given by
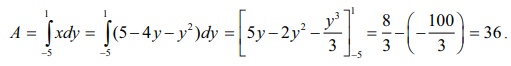
Note
As in
the previous problem, we again verify ArchimedesŌĆÖ formula that the area of the
parabolic arch is equal to two-thirds the base times the height.
Example 9.52
Find the
area of the region bounded by x ŌłÆ axis, the sine curve y
= sin x , the lines x = 0
and x = 2ŽĆ .
Solution
The required area is sketched in Fig. 9.21. One portion of the region lies above the x ŌłÆ axis between x = 0 and x = ŽĆ , and the other portion lies below x ŌłÆ axis between x = ŽĆ and x = 2ŽĆ .
So, the
required area is given by
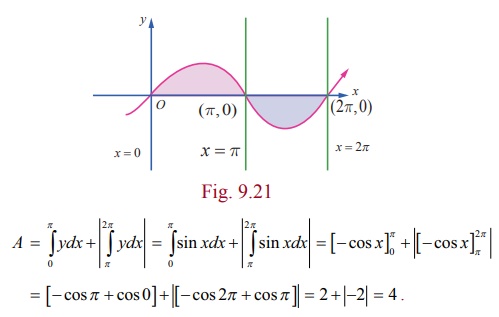
Note
If we
compute the definite integral 2ŽĆŌł½0sin xdx , we get
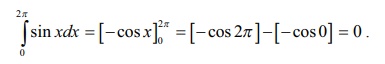
So 2ŽĆŌł½0
f (x)dx does not represent
the area of the region bounded by the curve
y = sin x , x ŌłÆ axis, the lines x = 0 and x = 2ŽĆ .
Example 9.53
Find the
area of the region bounded by x ŌłÆ
axis, the curve y =
|cos x|, the lines x = 0 and x = ŽĆ
.
Solution
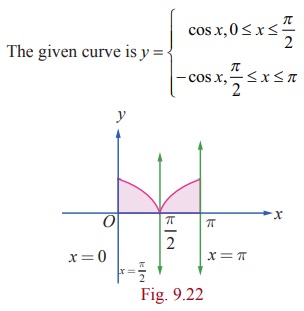
It lies
above the x ŌłÆ axis. The required area is sketched in Fig. 9.22. So, the
required area is given by
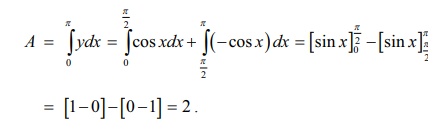
3. Area of the region bounded between two curves
Case
(i)
Let y = f
( x) and y = g( x) be the equations of two curves in the
XOY ŌłÆ plane such that f (x) Ōēź g ( x) for all x Ōłł [a, b] . We want to find the area A of
the region bounded between the two
curves, the ordinates x = a and x = b .
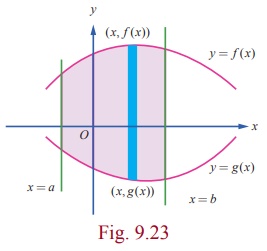
The
required area is sketched in Fig. 9.23. To compute A , we divide the region
into thin vertical strips of width Δx and
height f ( x) ŌłÆ g (
x) . It is important note that f (x) ŌłÆ g (x) Ōēź 0 for all x Ōłł[a,
b] . As before, the required area
is the limit of the sum of the areas of the vertical strips. Hence, we get
A = bŌł½a [ f (x) - g(x)]dx
Note
Viewing
in the positive direction of y ŌłÆ
axis, the curve y =
f ( x) can be termed as the upper curve (U) and the curve y = g(
x) as the lower curve (L). Thus, we
get A = bŌł½a [ yU ŌłÆ yL]dx
Case
(ii)
Let x = f ( y) and x = g( y) be the equations of two curves in the XOY ŌłÆ plane such that f ( y) Ōēź g ( y) for all y Ōłł[c, d ] . We want to find the area A of the region bounded between the two curves, the lines y = c and y = d . The required area is sketched in Fig. 9.24.
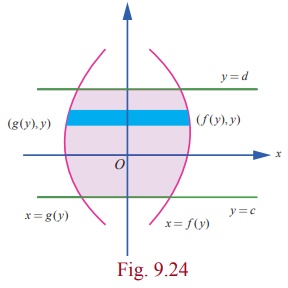
To compute A , we view in
the positive direction of the x ŌĆō
axis and divide the region into thin horizontal strips of width ╬öy and height f ( y) ŌłÆ g
( y) . It is important note that f ( y)
ŌłÆ
g ( y) Ōēź 0 for all y Ōłł[c,
d ] . As before, the required
area is the limit of the sum of the areas of the horizontal strips. Hence, we get
A = dŌł½c [ f (x) - g(x)]dx
Note
Viewing
in the positive direction of x ŌłÆ
axis, the curve x =
f ( y) can be termed as the right curve (R) and the curve x = f
( y) as the left curve (L). Thus, we
get A = bŌł½a [ xR ŌłÆ x
L ]dy .
Example 9.54
Find the
area of the region bounded between the parabolas y2 = 4x and x2 = 4y.
Solution
First,
we get the points of intersection of the parabolas. For this, we solve y2
= 4x and x2 = 4y simultaneously: Eliminating y between them, we get x4 =
64x and so x = 0 and x = 4 . Then the points of intersection
are (0, 0) and (4, 4) . The required region is sketched in Fig.9.25.
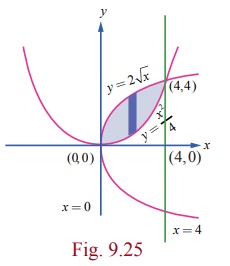
Viewing
in the direction of y -axis, the
equation of the upper boundary is y =
2ŌłÜx for 0 Ōēż x Ōēż 4 and the equation of the lower boundary is y = x2/4 for 0 Ōēż x Ōēż 4 . So, the required area ╬ö is
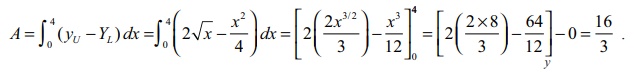
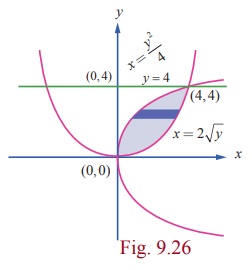
Note
Viewing
in the positive direction of x -axis,
the right bounding curve is x2
= 4y and the left bounding curve is y2 = 4x . See Fig. 9.26. The
equation of the right boundary is x =
2ŌłÜy for 0 Ōēż y Ōēż 4 and the equation of the left boundary is x = y2/4 for 0 Ōēż
y Ōēż 4 . So, the required area A is
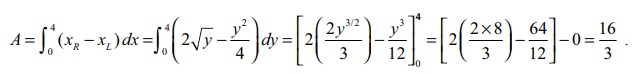
Example 9.55
Find the
area of the region bounded between the parabola x2 = y and the
curve y = |x|.
Solution
Both the
curves are symmetrical about y -axis.
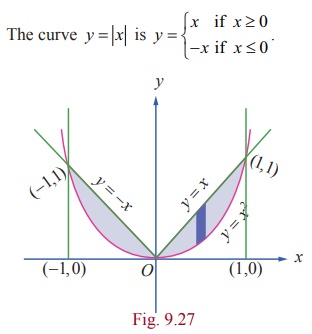
It
intersects the parabola x2
= y at ( 1,1) and ( ŌłÆ1, 1).
The area of the region bounded by the curves is sketched in Fig. 9.27. It lies in the first quadrant as well as in the second quadrant. By symmetry, the required area is twice the area in the first quadrant.
In the
first quadrant, the upper curve is y = x, 0 Ōēż x Ōēż 1 and the lower curve is y
= x2, 0 Ōēż x Ōēż 1. Hence,
the required area is given by
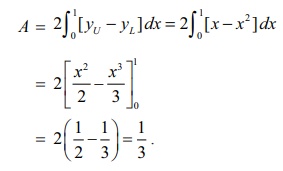
Example 9.56
Find the
area of the region bounded by y = cos
x, y = sin x, the lines x = ŽĆ/4 and x = 5ŽĆ/4.
Solution
The
region is sketched in Fig. 9.28. The upper boundary of the region is y = sin x for ŽĆ/4 Ōēż x Ōēż 5ŽĆ/4 and the lower boundary of the region is y = cos x for ŽĆ/4 Ōēż x Ōēż 5ŽĆ/4. So the required area A is given by
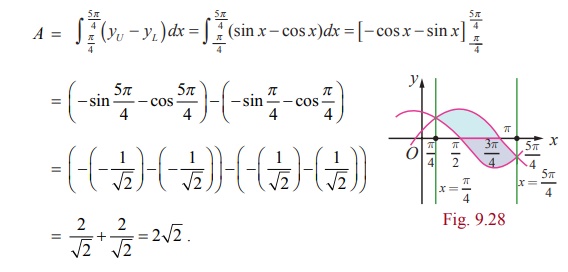
Example 9.57
The
region enclosed by the circle x2
+
y2 =
a2 is divided into two
segments by the line x =
h. Find the area of the smaller
segment.
Solution
The
smaller segment is sketched in Fig. 9.29. Here 0 < h < a
. By symmetry about the x -axis, the
area of the smaller segment is given by

Example 9.58
Find the
area of the region in the first quadrant bounded by the parabola y2 =
4x , the line x + y = 3 and y -axis.
Solution
First,
we find the points of intersection of x + y = 3 and y2 ŌłÆ 4x :
x + y = 3 ŌćÆ y = 3 ŌłÆ x .
Ōł┤ y 2 = 4x ŌćÆ (3 ŌłÆ x )2 = 4x
ŌćÆ x 2 ŌłÆ 10x + 9
= 0
ŌćÆ x = 1, x = 9 .
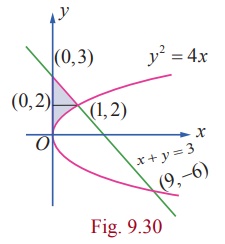
Ōł┤ x =1 in
x + y = 3 ŌćÆ y = 2 , and x = 9
in x + y = 3 ŌćÆ y = ŌłÆ6 .
Ōł┤(1,
2) and (9, ŌłÆ6) are the points of intersection.
The line
x + y
=
3 meets the y -axis at (0, 3) .
The
required area is sketched in Fig. 9.30.
Viewing
in the direction of y -axis, on the
right bounding curve is given by

Example 9.59
Find, by
integration, the area of the region bounded by the lines 5x ŌłÆ 2 y =
15, x + y
+
4 =
0 and the x-axis.
Solution
The
lines 5x ŌłÆ
2 y = 15, x + y +
4 =
0 intersect at (1, ŌłÆ5) . The line 5x ŌłÆ 2 y =
15 meets the x-axis at (
3, 0)
. The line x +
y + 4 = 0 meets the x-axis at ( ŌłÆ4, 0) . The required area is shaded in
Fig.9.31. It lies below the x-axis.
It can be computed either by considering vertical strips or horizontal strips.
When we
do by vertical strips, the region has to be divided into two sub-regions by the
line x = 1 . Then, we get

When we
do by horizontal strips, there is no need to subdivide the region. In this
case, the area is bounded on the right by the line 5x ŌłÆ 2 y =
15 and on the left by x +
y + 4 = 0 . So, we get
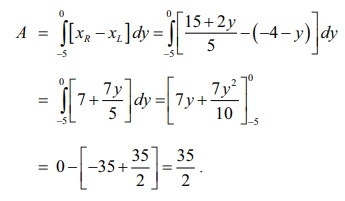
Note
The
region is triangular with base 7 units and height 5 units. Hence its area is
35/2 without using integration.
Example 9.60
Using
integration find the area of the region bounded by triangle ABC, whose vertices A, B, and C are (
ŌłÆ1,1),
(
3, 2)
, and (
0, 5)
respectively.
Solution
See Fig.
9.32.

Example 9.61
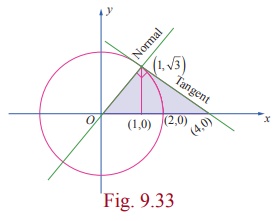
Using
integration, find the area of the region which is bounded by x-axis, the tangent and normal to the
circle x2 + y2 = 4 drawn at (1, ŌłÜ3) .
Solution
We recall
that the equation of the tangent to the circle x2 + y2= a2 at ( x1 , y1 ) is xx1 + yy1 = a2 .
So, the equation of the tangent to the circle x2 + y2 = 4 at
(1,
ŌłÜ3)
is x + y
ŌłÜ3 =
4 ; that is, y = ŌłÆ 1/ŌłÜ3 (x
ŌłÆ
4) . The tangent meets the x-axis at
the point (4,0). The slope of the tangent is ŌĆō1/ŌłÜ3. So the slope of
the normal is ŌłÜ3 and hence equation of the normal is y ŌłÆ ŌłÜ3 = ŌłÜ3( x ŌłÆ1) ; that is y = ŌłÜ3x and it passes through the origin. The
area to be found is shaded in the adjoining figure. It can be found by two
methods.
Method 1
Viewing
in the postive direction of y-axis,
the required area is the area of the region bounded by x-axis, y =
ŌłÜ3x and x + y ŌłÜ3 =
4 . So it can be obtained by applying the formula bŌł½a ydx
. For this, we have to split the region into sub-regions, one sub-region
bounded by x-axis, the normal y = ŌłÜ3x and the line x = 1 ; the other
sub-region bounded by x-axis, the
tangent x + yŌłÜ3= 4 and the line x = 1 axis.
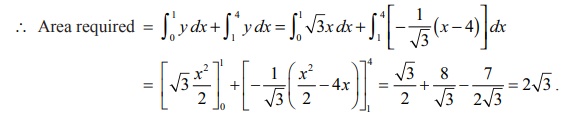
Method 2
Viewing
in the direction of x-axis, the
required area is the area of the region bounded between y = ŌłÜ3x and x + yŌłÜ3 = 4 , y = 0
and y = ŌłÜ3. So, it can be obtained by applying the formula
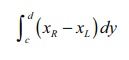
Here, c = 0 , d = ŌłÜ3 , xR
is the x-value on the tangent x + yŌłÜ3
=
4 and xL is the x-value on the normal y = ŌłÜ3x .
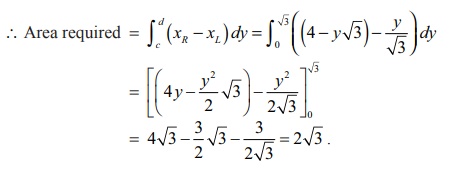
Working rule for finding area of the region bounded by y = f1(x), y = f2(x), the lines x = a and x = b , where a < b :
Draw an
arbitrary line parallel to y-axis
cutting the plane region. First, find the y-coordinate
of the point where the line enters the region. Call it yENTRY . Next, find the y-coordinate of the point where the line exits the region. Call it yEXIT . Both yENTRY and yEXIT can be found from the equations
of the bounding curves. Then, the required area is given by bŌł½a [ y
EXIT ŌłÆ
yENTRY ]dx.
Working rule for
finding area of the region bounded by x
= g1(y), x = g2(y), the lines y = c and y = d , where c < d :
Draw an
arbitrary line parallel to x-axis
cutting the plane region.
First,
find the x-coordinate of the point where
the line enters the region. Call it xENTRY
.
Next,
find the x-coordinate of the point
where the line exits the region. Call it xEXIT
. Both xENTRY and xEXIT can be found from the
equations of the bounding curves. Then, the required area is given by dŌł½c [ x
EXIT ŌłÆ
xENTRY ]dy .
Related Topics