Applications of Integration | Mathematics - Gamma Integral | 12th Maths : UNIT 9 : Applications of Integration
Chapter: 12th Maths : UNIT 9 : Applications of Integration
Gamma Integral
Gamma Integral
In this
section, we study about a special improper integral of the form Ōł×Ōł½0 e
ŌłÆx xnŌłÆ1dx , where n is a positive integer. Here, we have
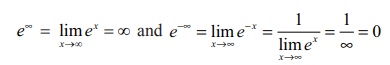
By
LŌĆÖHo╦åpitalŌĆÖsŌĆē rule, for every positive integer m , we get,
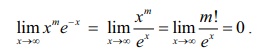
Example 9.43
Prove
that Ōł×Ōł½0 eŌłÆx xn
dx = n!, where n is a positive integer.
Solution
Applying
integration by parts, we get
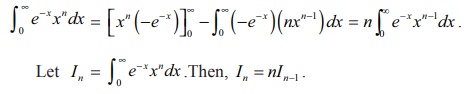
Let In =
Ōł×Ōł½0 eŌłÆx xn dx .Then, In = nInŌłÆ1
.
So, we
get In = n ( n ŌłÆ1)InŌłÆ2 .
Proceeding
in this way, we get ultimately,
In = n ( n ŌłÆ 1)( n ŌłÆ 2) ( 2)(1)I0 .
But, I0 =
Ōł×Ōł½0 e
ŌłÆx x0dx = ( ŌłÆeŌłÆx)Ōł×0 = 0 +1 = 1 . So, we get In = n
(n ŌłÆ 1)(n ŌłÆ 2) (2)(1) = n!.
Hence,
we get
Result
Ōł×Ōł½0 e ŌłÆx xn
dx =
n!, where n is a nonnegative
integer.
Note
The
integral Ōł×Ōł½0 eŌłÆx xnŌłÆ1dx defines a unique positive integer
for every positive integer n Ōēź
1.
Definition 9.1
Ōł×Ōł½0 e ŌłÆx xnŌłÆ1dx is called the gamma integral. It is denoted by ╬ō(n) and
is read as ŌĆ£gamma of n ŌĆØ.
Note
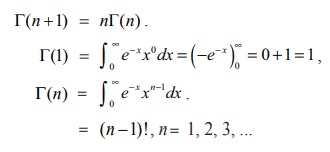
Example 9.44
Evaluate
Ōł×Ōł½0 e
ŌłÆax xn
dx ,where a > 0 .
Solution
Making
the substitution t =
ax , we get dt = adx
and x = 0 ŌćÆ t
=
0 and x = Ōł×
ŌćÆ t
= Ōł×
.
Hence, we
get
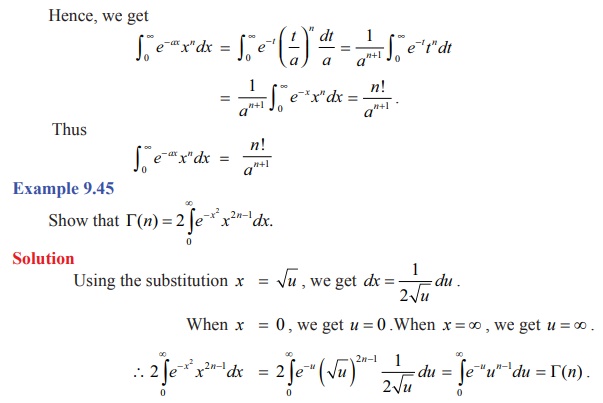

Related Topics