Applications of Integration | Mathematics - Improper Integrals | 12th Maths : UNIT 9 : Applications of Integration
Chapter: 12th Maths : UNIT 9 : Applications of Integration
Improper Integrals
Improper Integrals
In
defining the Riemann integral aŌł½b f
( x)dx , the interval [a , b] of integration is finite and f ( x)
is finite at every point in [a , b] . In many physical applications, the
following types of integrals arise:
aŌł½Ōł× f (
x) dx , aŌł½ŌłÆ Ōł× f (
x) dx , Ōł×Ōł½ŌłÆŌł× f (
x) dx ,

where a is a real number and f ( x)
is a continuous function on the interval of integration. They are defined as
the limits of Riemann integrals as follows:
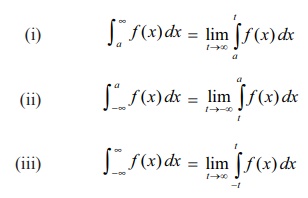
They are
called improper integrals of first kind.
If the limits exist, then the improper integrals
are said to be convergent.
Note
By the
Fundamental theorem of integral calculus, there exists a function F (t)
such that
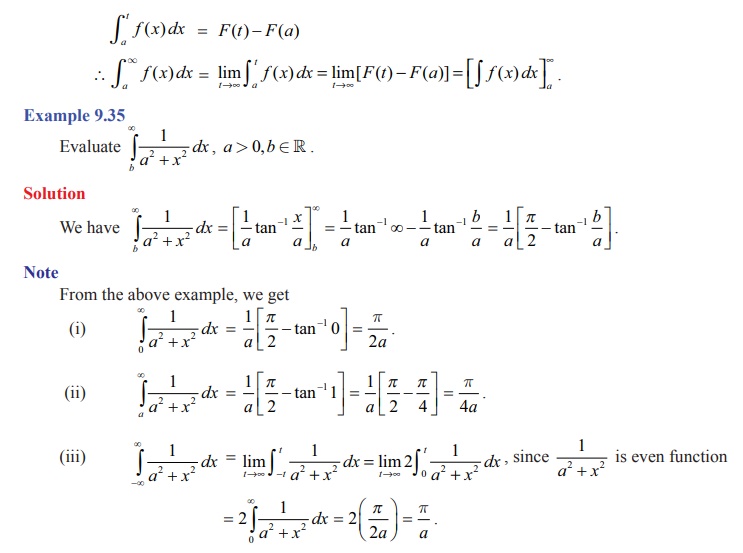

Related Topics