Applications of Integration | Mathematics - Reduction Formulae | 12th Maths : UNIT 9 : Applications of Integration
Chapter: 12th Maths : UNIT 9 : Applications of Integration
Reduction Formulae
Reduction Formulae
Certain
definite integrals can be evaluated by an index-reduction method. In this
section, we obtain the values of the following definite integrals:
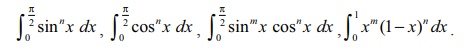
We also
obtain the value of the improper integral Ōł×Ōł½0 eŌłÆx xn
dx .
The
method of obtaining a reduction formula has the following steps:
Step 1 : Identify an index (positive
integer) n in the integral.
Step 2 : Put the integral as In.
Step 3 : Applying integration by parts,
obtain the equation for In in terms of InŌłÆ1 or InŌłÆ2.
The
resulting equation is called the reduction formula for In.
We list
below a few reduction formulae without proof:
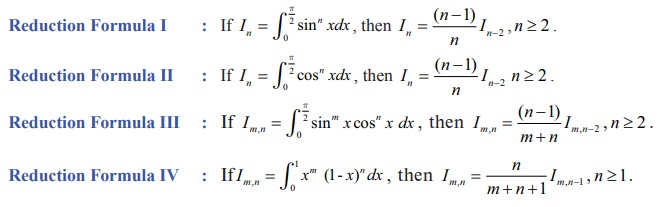
Using
the reduction formulas I and II, we obtain the following result (stated without
proofs):

By
applying the reduction formula III iteratively, we get the following results
(stated without proof):
(i) If n is even and m is even,
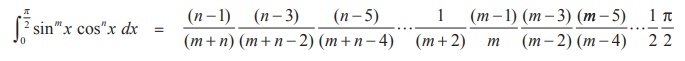
(ii) If n is odd and m is any positive integer (even or odd), then
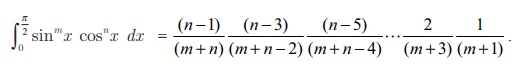
Note
If one
of m and n is odd, then it is convenient to get the power of cos x as odd. For instance, if m is odd and n is even, then
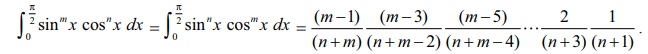
Example 9.39
Find the
values of the following:
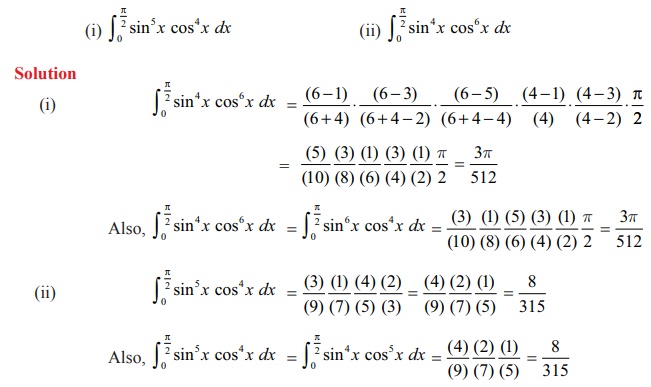
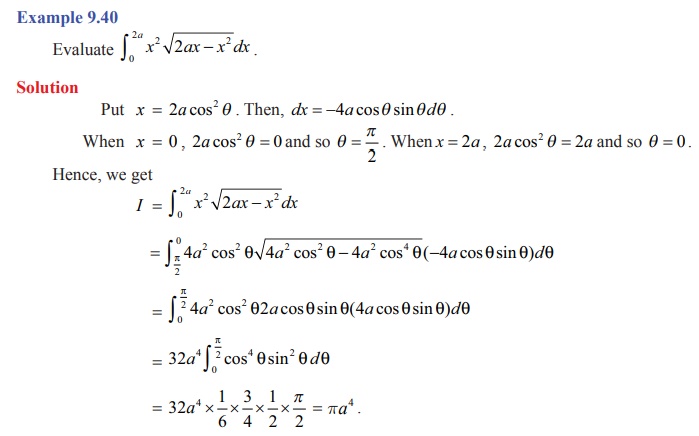

By
applying the reduction formula III iteratively, we get the following results
(stated without proof):
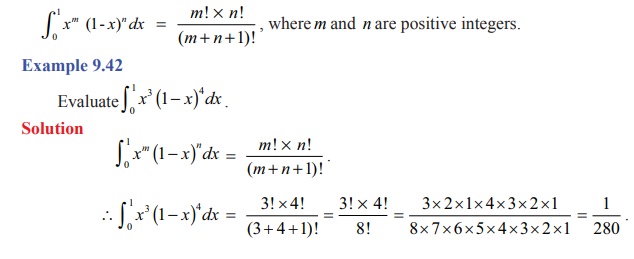
Related Topics