Verifying the Method

Verifying the Method

After developing and optimizing a method, it is necessary to determine the quality of results that can reasonably be expected when the method is used by a single ana- lyst. Generally, three steps are included in the process of verifying a method: deter- mining single-operator characteristics, the blind analysis of standards, and deter- mining the method’s ruggedness. In addition, if an alternative standard method exists, both the standard method and the new method can be used to analyze the same sample, and the results compared. If the quality of the results is unacceptable, the method is not suitable for consideration as a standard method.

Single-Operator Characteristics

The first step in verifying a method is to determine the precision, accuracy, and de- tection limit when a single analyst uses the method to analyze a standard sample of known composition. The detection limit, which was discussed, is de- termined by analyzing a reagent blank for each type of sample matrix for which the method will be used. Precision is determined by analyzing replicate portions, preferably more than ten, of a standard sample. Finding the method’s accuracy is evaluated by a t-test. Precision and accuracy should be evaluated for several different concentration levels of analyte, including at least one concentration near the detection limit, and for each type of sample matrix that will be encountered. The analysis of several concentrations allows for the detection of constant sources of determinate error and establishes the range of concentrations for which the method is applicable.

Blind Analysis of Standard Samples

Single-operator characteristics are determined by analyzing a sample whose concen- tration of analyte is known to the analyst. The second step in verifying a method is the blind analysis of standard samples where the analyte’s concentration remains unknown to the analyst. The standard sample is analyzed several times, and the av- erage concentration of the analyte is determined. This value should be within three, and preferably two standard deviations (as determined from the single-operator characteristics) of the analyte’s known concentration.

Ruggedness Testing

In many cases an optimized method may produce excellent results in the laboratory developing the method, but poor results in other laboratories. This is not surprising since a method is often optimized by a single analyst under an ideal set of condi- tions, in which the sources of reagents, equipment, and instrumentation remain the same for each trial. The procedure might also be influenced by environmental fac- tors, such as the temperature or relative humidity in the laboratory, whose levels are not specified in the procedure and which may differ between laboratories. Finally, when optimizing a method the analyst usually takes particular care to perform the analysis in exactly the same way during every trial.

An important step in developing a standard method is to determine which fac- tors have a pronounced effect on the quality of the analytical method’s result. The procedure can then be written to specify the degree to which these factors must be controlled. A procedure that, when carefully followed, produces high-quality results in different laboratories is considered rugged. The method by which the critical fac- tors are discovered is called ruggedness testing.

Ruggedness testing is often performed by the laboratory developing the stan- dard method. Potential factors are identified and their effects evaluated by perform- ing the analysis while the factors are held at two levels. Normally one level for each factor is that given in the procedure, and the other is a level likely to be encountered when the procedure is used by other laboratories.

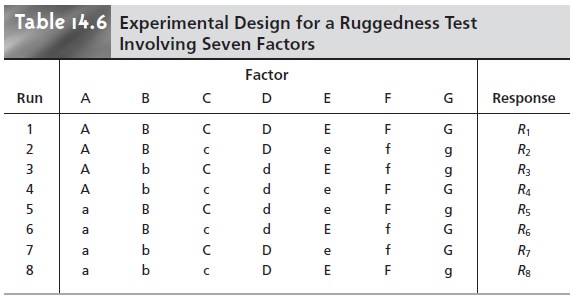
This approach to ruggedness testing can be time-consuming. If seven poten- tial factors are identified, for example, ruggedness testing can be accomplished with a 27 factorial design. This requires a total of 128 trials, which is a prohibitively large amount of work. A simpler experimental design is shown in Table 14.6, in which the two factor levels are identified by upper case and lower case letters. This design, which is similar to that for the 23 factorial design discussed in the previous section, is called a fractional factorial design and provides information about the first-order effect of each factor. It does not, however, provide suffi- cient information to evaluate higher order effects or potential interactions be- tween factors, both of which are assumed to be of less importance than first- order effects.

The experimental design for ruggedness testing is balanced in that each factor level is paired an equal number of times with the upper case and lower case levels for every other factor. The effect of changing the level for any one factor, E_f, is de- termined by subtracting the average response when the factor is at its upper case level from the average value when it is at its lower case level

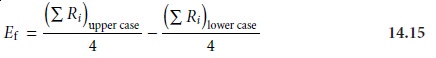
Because the design is balanced, the levels for the remaining factors appear an equal number of times in both summation terms, and, consequently, their effect on the response is canceled. For example, the effect of changing the level for fac- tor A is determined by averaging the responses from runs 1 through 4 and sub- tracting the average response from runs 5 through 8. Factor B does not affect E_f because its upper case levels in runs 1 and 2 are canceled by the upper case levels in runs 5 and 6, and its lower case levels in runs 3 and 4 are canceled by the lower case levels in runs 7 and 8. Similar reasoning shows that the remaining factors are also canceled.

After each of the effects is calculated, they are ranked from largest to smallest, without regard to sign, and those factors whose effects are substantially larger than the other factors are identified. The estimated standard deviation for the analysis is given by

This provides the best estimate of the expected standard deviation for results ob- tained by several laboratories, due to the effects of small changes in uncontrolled or poorly controlled factors. If this standard deviation is unacceptably large, then the procedure may be modified to bring under greater control those factors whose lev- els have the greatest effect on the response.

Equivalency Testing

If a standard method is available, the performance of a new method can be evalu- ated by comparing results with those obtained with an approved standard method. The comparison should be done at a minimum of three concentrations to evaluate the applicability of the new method for different amounts of analyte. Alternatively, we can plot the results obtained by the new method against those obtained by the approved standard method. A linear regression analysis should give a slope of 1 and a y-intercept of 0 if the results of the two methods are equivalent.