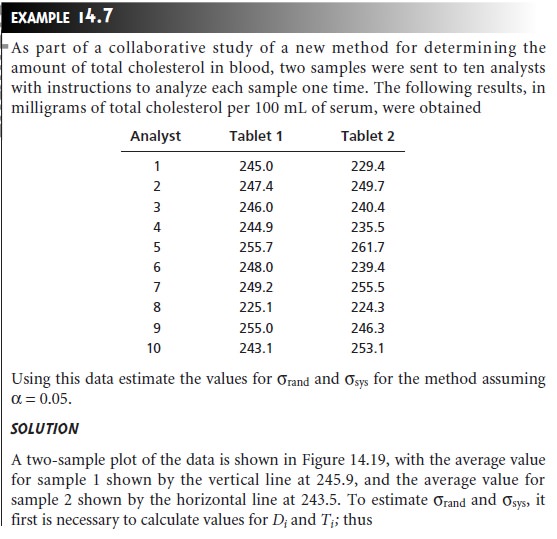
Chapter: Modern Analytical Chemistry: Developing a Standard Method
Two-Sample Collaborative Testing
Two-Sample Collaborative Testing
The design of a collaborative test must provide
the additional information needed to separate the effect of random error from that due to systematic errors intro-
duced by the analysts. One simple approach,
which is accepted
by the Association of Official Analytical Chemists, is to have each analyst analyze
two samples, X and
Y, that are similar in both matrix
and concentration of analyte. The results ob- tained by each analyst
are plotted as a single
point on a two-sample chart,
using the result for
one sample as the x-coordinate and
the value for
the other sample
as the y-coordinate.8,9
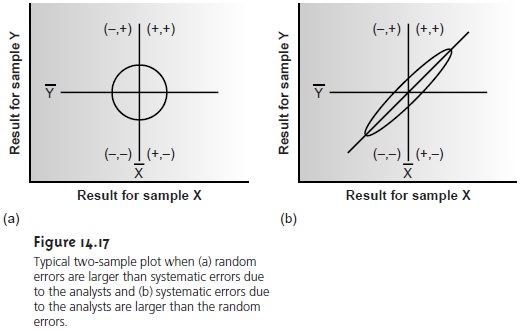
A two-sample chart is divided into four quadrants, identified as (+, +), (–, +), (–, –), and (+, –), depending on whether the points in the quadrant have values for the two samples that are larger or smaller than the mean values for samples X and Y. Thus, the quadrant (+, –) contains all points for which the result for sample X is larger than the mean for sample X, and for which the result for sample Y is less than the mean for sample Y.
If the variation in results is dominated by random errors, then the points
should be distributed randomly in all four quadrants, with an equal number of points in each quadrant. Furthermore, the points
will be clustered in a circular pattern
whose center is the mean values for the two samples (Figure
14.17a). When systematic errors are significantly larger than random errors, then the points will be found
primarily in the (+, +) and (–, –) quadrants and will be clus-
tered in an elliptical pattern
around a line bisecting these
quadrants at a 45° angle (Figure 14.17b).
A visual inspection of a two-sample chart provides an
effectivemeans for qualitatively evaluating the results obtained by each
analyst
and of the capabilities of a proposed
standard method. If no random errors are present, then all points
will be found
on the 45° line. The length of a perpendicular line from any
point to the
45° line, there- fore, is proportional to the effect
of random error
on that analyst’s re- sults (Figure 14.18).
The distance from
the intersection of the lines
for the mean values
of samples X and Y, to the perpendicular projection of a point on the 45°
line, is proportional to the analyst’s systematic error (Figure 14.18).
An ideal standard method is characterized by small random errors and small systematic errors due to the analysts and should show a compact clustering of points that is more circular
than elliptical.

The data used to construct a two-sample chart
can also be used to separate the total variation of the
data, σtot, into
contributions from random
error, σrand, and systematic errors due to the analysts, σsys. Since an analyst’s systematic errors should be present at the same
level in the
analysis of samples
X and Y, the differ- ence, D, between the results
for the two
samples
Di = Xi – Yi
is influenced only
by random error.
The contribution from
random error, there- fore, is estimated by the standard deviation of the
differences for each
analyst
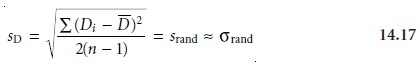
where n is the
number of analysts. The inclusion of a factor
of 2 in the denominator of equation 14.17 is the result
of using two
values to determine Di. The
total, T, of each analyst’s results for the two samples
Ti = Xi + Yi
contains contributions from both random error and twice the analyst’s systematic error; thus

The standard deviation of the totals provides an estimate for σtot.
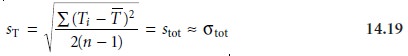
Again, the factor
of 2 in the denominator is the result
of using two
values to deter- mine Ti.
If systematic errors
due to the analysts are significantly larger
than random er- rors, then sT
should be larger
than sD. This can be tested
statistically using a one-
tailed F-test
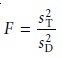
where the degrees
of freedom for both the numerator and the denominator are n –
1. If sT is significantly larger
than sD, then we can use
equation 14.18 to separate
the data’s total variation into that due to random
error and that due to the system- atic errors of the analysts.

When the true
values for the
two samples are
known, it is possible to test for the
presence of systematic errors in the method. If no systematic method errors occur, then the sum of the true values
for the samples,
μtot
μtot = μsamp X + μsamp Y
will fall within the confidence interval around the average value, T’. A two-tailed t-test, with the following null and alternative hypotheses
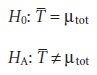
is used to determine whether
there is any
evidence for systematic method errors. The test statistic, texp, is given as

and has n –
1 degrees of freedom. The Rt[2] in the denominator is included because
sT, as given
in equation 14.19,
underestimates the standard
deviation when comparing T’ to μtot.

In Examples 14.7 and 14.8 we have seen how a collaborative test using a pair of closely related samples can
be used to evaluate a method. Ideally, a collaborative test should involve several pairs of samples,
whose concentrations of analyte span the
method’s anticipated useful
range. In this way the method can be evaluated for con- stant sources
of error, and the expected
relative standard deviation and bias for dif-
ferent levels of analyte can
be determined.
Related Topics