Chapter: Operations Research: An Introduction : Modeling with Linear Programming
Two-Variable LP Model
TWO-VARIABLE
LP MODEL
This
section deals with the graphical solution of a two-variable LP. Though
two-variable problems hardly exist in practice, the treatment provides concrete
foundations for the development of the general simplex algorithm presented in
Chapter 3.
Example
2.1-1 (The Reddy Mikks Company)
Reddy
Mikks produces both interior and exterior paints from two raw materials, Ml and
M2. The
following table provides the basic data of the problem:

A market
survey indicates that the daily demand for interior paint cannot exceed that
for exterior paint by more than 1 ton. Also, the maximum daily demand for
interior paint is 2 tons.
Reddy Mikks
wants to determine the optimum (best) product mix of interior and exterior
paints that maximizes the total daily profit.
The LP
model, as in any OR model, has three basic components.
1. Decision variables that we seek to determine.
2. Objective (goal) that we need to optimize
(maximize or minimize).
3.Constraints that the solution must satisfy.
The
proper definition of the decision variables is an essential first step in the
development of the model. Once done, the task of constructing the objective
function and the constraints becomes more straightforward.
For the
Reddy Mikks problem, we need to determine the daily amounts to be produced of
exterior and interior paints. Thus the variables of the model are defined as
x1 = Tons
produced daily of exterior paint
x2 = Tons
produced daily of interior paint
To
construct the objective function, note that the company wants to maximize (i.e., increase as much as
possible) the total daily profit of both paints. Given that the profits per ton
of exteri-or and interior paints are 5 and 4 (thousand) dollars,
respectively, it follows that
Total
profit from exterior paint = 5x1
(thousand) dollars
Total
profit from interior paint = 4X2
(thousand) dollars
Letting z represent the total daily profit (in
thousands of dollars), the objective of the company is
Maximize
z = 5X1
+ 4X2
Next, we
construct the constraints that restrict raw material usage and product demand.
The raw material restrictions are expressed verbally as
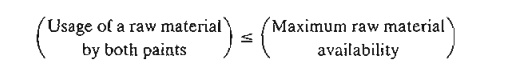
The daily
usage of raw material MI is 6 tons
per ton of exterior paint and 4 tons per ton of inte-rior paint. Thus
Usage of
raw material M1 by exterior paint = 6X1 tons/day
Usage of
raw material M1 by interior paint = 4X2 tons/day
Hence
Usage of
raw material M1 by both paints = 6X1 + 4x2 tons/day
In a
similar manner,
Usage of
raw material M2 by both paints = IX1 + 2X2 tons/day
Because
the daily availabilities of raw materials M1 and M2 are limited to 24 and 6 tons,
respectively, the associated restrictions are given as
6x1 + 4x2 <= 24 (Raw
material M1)
x1 + 2x2 <=6 (Raw material M2)
The first
demand restriction stipulates that the excess of the daily production of
interior over exterior paint, X2 - Xl, should
not exceed 1 ton, which translates to
x2
– x1 =< 1 (Market limit)
The
second demand restriction stipulates that the maximum daily demand of interior
paint is limited to 2 tons, which translates to
x2 =< 2 (Demand limit)
An
implicit (or "understood-to-be") restriction is that variables xl
and x2 cannot assume
negative values. The non negativity restrictions, x1>= 0, x2 > = 0, account for this requirement.
The
complete Reddy Mikks model is
Maximize
z = 5x1 + 4x2
subject
to
6xI + 4x2 <= 24 (1)
xI
+ 2x2 =< 6 (2)
-x1
+x2 <= 1 (3)
X2
<= 2 (4)
x1,x2
>= 0 (5)
Any
values of x1 and x2
that satisfy all five constraints
constitute a feasible solution. Otherwise, the solution is infeasible. For
example, the solution, x1 = 3 tons per day and x2 = I ton per day, is feasible because it does not
violate any of the constraints, including the nonnegativity restrictions. To verify
this result, substitute (x1 = 3, x2
= 1) in the left-hand side of each constraint. In constraint (1) we have 6x1
+ 4x2 = 6 x 3 + 4 X 1 == 22, which is less than the
right-hand side of the constraint (= 24). Constraints 2 through 5 will yield
similar conclusions (verify!). On the other hand, the solution x1 = 4 and x2 = 1 is infeasible because
it does not satisfy constraint (I)-namely, 6 X 4 + 4 X 1 = 28, which is larger than the right-hand
side (= 24).
The goal
of the problem is to find the best feasible
solution, or the optimum, that maximizes the total profit. Before we can do
that, we need to know how many feasible
solutions the Reddy Mikks problem has. The answer, as we will see from the
graphical solution in Section 2.2, is "an infinite number," which
makes it impossible to solve the problem by
enumeration. Instead, we need a systematic procedure that will locate the
optimum solution in a finite num-ber of steps. The graphical method in Section
2.2 and its algebraic generalization in Chapter 3 will explain how this can be
accomplished.
Properties of the LP Model. In
Example 2.1-1, the objective and the constraints are all linear functions. Linearity implies that the LP must satisfy
three basic properties:
1. Proportionality: This
property requires the contribution of each decision variable in both the
objective function and the constraints to be directly proportional to the value of the variable. For example, in
the Reddy Mikks model, the quantities 5x1 and 4x1 give the profits for producing x1
and x2 tons of
exterior and in- 2.2 terior paint, respectively, with the unit profits per ton,
5 and 4, providing the constants of proportionality. If, on the other hand, Reddy Mikks
grants some sort of quantity discounts when sales exceed certain amounts, then
the profit will no longer be proportional to the production amounts, x1
and x2, and the profit function becomes
nonlinear.
2. Additivity: This property requires the total
contribution of all the variables in the objective function and in the
constraints to be the direct sum of the individual contributions of each
variable. In the Reddy Mikks model, the total profit equals the sum of the two
individual profit components. If, however,
the two products compete for market
share in such a way that an increase in sales of one adversely affects the
other, then the additivity property is not satisfied and the model is no longer
linear.
3. Certainty: All the objective and constraint
coefficients of the LP model are deterministic. This means that they are known
constants-a rare occurrence in real life, where data are more likely to be
represented by probabilistic distributions. In essence, LP coefficients are
average-value approximations of the probabilistic distributions. If the standard deviations of these
distributions are sufficiently small, then the approximation is acceptable.
Large standard deviations can be accounted for directly by using stochastic LP
algorithms (Section 19.2.3) or indirectly by applying sensitivity analysis to
the optimum solution (Section 3.6).
PROBLEM
SET 2.1A
1. For
the Reddy Mikks model, construct each of the following constraints and express
it with a linear left-hand side and a constant right-hand side:
(a) The
daily demand for interior paint exceeds that of exterior paint by at least 1 ton.
(b) The
daily usage of raw material M2 in tons is at most 6 and at least
3.
(c) The
demand for interior paint cannot be less than the demand for exterior paint.
(d) The
minimum quantity that should be produced of both the interior and the exterior
paint is 3 tons.
(e) The
proportion of interior paint to the total production of both interior and
exterior paints must not exceed .5.
2. Determine
the best feasible solution among the
following (feasible and infeasible) solutions of the Reddy Mikks model:
(a) x1
= 1, x2 = 4
(b) x1
= 2, x2 = 2
(c) x1
=3, x3 = 1.5
(d) x1
= 2, x2 = 1
(e) x1
=2, x2 = -1
3. For
the feasible solution x1=2, x2=2
of the Reddy Mikks model, determine the unused amounts of raw materials Ml and M2.
4. Suppose
that Reddy Mikks sells its exterior paint to a single wholesaler at a quantity
discount.The profit per ton is $5000 if the contractor buys no more than 2 tons
daily and $4500 otherwise. Express the objective function mathematically. Is
the resulting function linear?
Related Topics