Selected LP Applications: Currency Arbitrage

2. Currency Arbitrage

In today's global economy, a multinational company must deal with currencies of the countries in which it operates. Currency arbitrage, or simultaneous purchase and sale of currencies in different markets, offers opportunities for advantageous movement of money from one currency to another. For example, converting £1000 to U.S. dollars in 2001 with an exchange rate of $1.60 to £1 will yield $1600. Another way of making the conversion is to first change the British pound to Japanese yen and then convert the yen to U.S. dollars using the 2001 exchange rates of £1 = ¥175 and $1 = ¥105. The resulting dollar amount is (£1,000x¥175) / ¥105 = $ 1,666,.67. This example demonstrates the advantage of converting the British money first to Japanese yen and then to dollars. This section shows how the arbitrage problem involving many currencies can be formulated and solved as a linear program.

Example 2.3-2   (Currency Arbitrage Model)

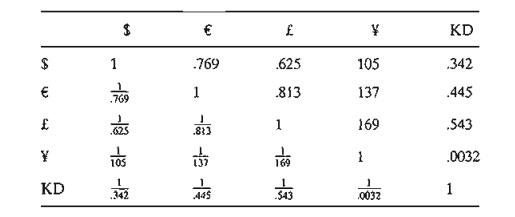
Suppose that a company has a total of 5 million dollars that can be exchanged for euros (€), British pounds (£), yen (¥), and Kuwaiti dinars (KD). Currency dealers set the following limits on the amount of any single transaction: 5 million dollars, 3 million euros, 3.5 million pounds, 100 million yen, and 2.8 million KDs. The table below provides typical spot exchange rates. The bottom diagonal rates are the reciprocal of the top diagonal rates. For example, rate(€→ $) = l/rate( $ → €) = 1/.769 = 1.30.

Is it possible to increase the dollar holdings (above the initial $5 million) by circulating currencies through the currency market?

Mathematical Model: The situation starts with $5 million. This amount goes through a number of conversions to other currencies before ultimately being reconverted to dollars. The problem thus seeks determining the amount of each conversion that will maximize the total dollar holdings.

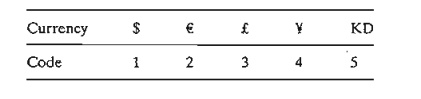
For the purpose of developing the model and simplifying the notation, the following nu-meric code is used to represent the currencies.

Define

xij = Amount in currency i converted to currency j, i and j  = 1,2, ... ,5

For example, x₁₂ is the dollar amount converted to euros and x₅₁ is the KD amount converted to dollars. We further define two additional variables representing the input and the output of the arbitrage problem:

I  = Initial dollar amount (= $5 million)

y = Final dollar holdings (to be determined from the solution)

Our goal is to determine the maximum final dollar holdings, y, subject to the currency flow restrictions and the maximum limits allowed for the different transactions.

Definition of the input/output variable, x₁₃,  between $ and £

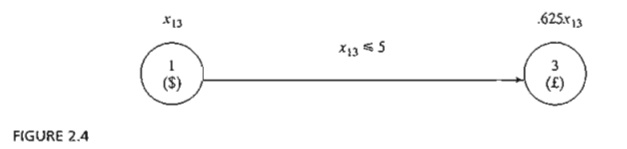
We start by developing the constraints of the model. Figure 2.4 demonstrates the idea of converting dollars to pounds. The dollar amount x_I3 at originating currency 1 is converted to 625x_l3 pounds at end currency 3.At the same time, the transacted dollar amount cannot exceed the limit set by the dealer, x₁₃ ≤ 5.

To conserve the flow of money from one currency to another, each currency must satisfy the following input-output equation:

( Total sum available of a currency (input) ) = ( Total sum converted to other currencies (output) )

1. Dollar (i = 1):

Total available dollars = Initial dollar amount + dollar amount from other currencies

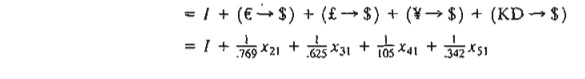
Total distributed dollars = Final dollar holdings + dollar amount to other currencies

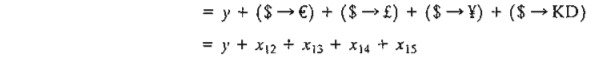
Given I = 5, the dollar constraint thus becomes

3.    Pound (i = 3):

Total available pounds = ($ -→ £)  + (€→ £)  + (¥→ £) + (KD → £)

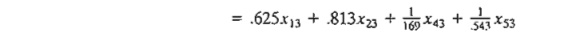
Total distributed pounds = (£→ $)  + (£→ €) + (£→ ¥)  + (£→ KD)

= x₃₁ + x₃₂ +x₃₄ + x₃₅

Thus, the ,constraint is

The only remaining constraints are the transaction limits, which are 5 million dollars, 3 million euros,3.5 million pounds, 100 million yen, and 2.8 million KDs. These can be translated as

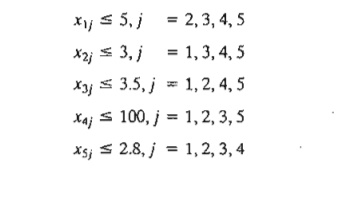
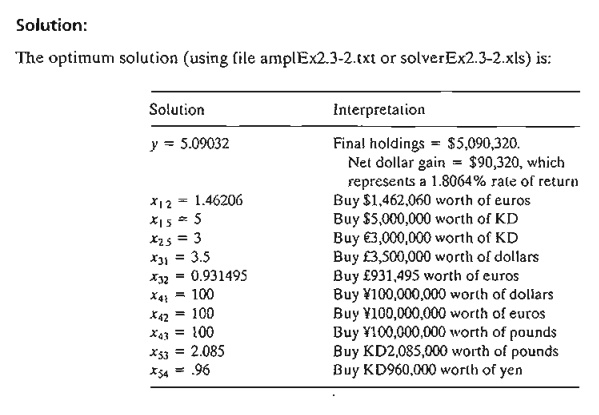
Remacks. At first it may appear that the solution is nonsensical because it calls for using x_l2 + x₁₅ = 1.46206 + 5 = 6.46206, or $6,462,060 to buy euros and KDs when the initial dollar amount is only $5,000,000. Where do the extra dollars come from? What happens in practice is that the given solution is submitted to the currency dealer as one order, meaning we do not wait until we accumulate enough currency of a certain type before making a buy. In the end, the net result of all these transactions is a net cost of $5,000,000 to the investor. This can be seen by sum-ming up all the dollar transactions in the solution:

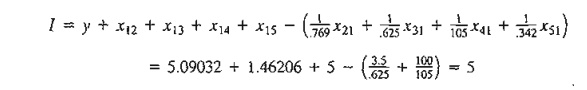
Notice that x₂₁, x₃₁ , x₄₁ and x₅₁ are in euro, pound, yen, and KD, respectively, and hence must be converted to dollars.

PROBLEM SET 2.3B

 1. Modify the arbitrage model to account for a commission that amounts to.1 % of any currency buy. Assume that the commission does not affect the circulating funds and that it is collected after the entire order is executed. How does the solution compare with that of the original model?

2. Suppose that the company is willing to convert the initial $5 million to any other currency that will provide the highest rate of return. Modify the original model to determine which currency is the best.

3. Suppose the initial amount I = $7 million and that the company wants to convert it optimally to a combination of euros, pounds, and yen. TIle final mix may not include more than €2 million, £3 million, and ¥200 million. Modify the original model to determine the optimal buying mix of the three currencies.

4. Suppose that the company wishes to buy $6 million. The transaction limits for different currencies are the same as in the original problem. Devise a buying schedule for this trans-action, given that mix may not include more than €3 million, £2 million, and KD2 million.

5. Suppose that the company has $2 million, £5 million, £4 million. Devise a buy-sell order that will improve the overall holdings converted to yen.