Graphical LP Solution: Solution of a Minimization Model

GRAPHICAL LP SOLUTION

The graphical procedure includes two steps:

                                             1. Determination of the feasible solution space.

                                             2. Determination of the optimum solution from among all the feasible points in the solution space.

The procedure uses two examples to show how maximization and minimization objective functions are handled.

2. Solution of a Minimization Model

Example 2.2-2  (Diet Problem)

Ozark Farms uses at least 800 lb of special feed daily. The special feed is a mixture of corn and soybean meal with the following compositions:

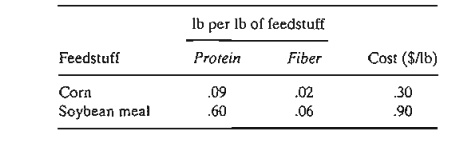
The dietary requirements of the special feed are at least 30% protein and at most 5% fiber. Ozark Farms wishes to determine the daily minimum-cost feed mix.

Because the feed mix consists of corn and soybean meal, the decision variables of the model are defined as

x₁ = lb of corn in the daily mix

x₂      = lb of soybean meal in the daily mix

The objective function seeks to minimize the total daily cost (in dollars) of the feed mix and is thus expressed as

Minimize z= 3x₁ +9x₂

The constraints of the model reflect the daily amount needed and the dietary requirements. Because Ozark Farms needs at least 800 Ib of feed a day, the associated constraint can be expressed as

x₁+x₂ > =800

As for the protein dietary requirement constraint, the amount of protein included in x₁ lb of corn and x₂ lb of soybean meal is (.09x₁ + .6x₂) lb. This quantity should equal at least 30% of the total feed mix (x₁ + x₂) lb-that is,

.09x₁ + .6x₂ >= .3(x₁+x₂)

In a similar manner, the fiber requirement of at most 5% is constructed as

.02x₁ + .06x₂ <= .05(x₁+x₂)

The constraints are simplified by moving the terms in x₁ and x₂ to the left-hand side of each inequality, leaving only a constant on the right-hand side. The complete model thus becomes

Minimize z= .3x₁ + .9x₂

Subject to

x₁+x₂ >= 800

.21x₁ - .30x₂ <= 0

.03x1 - .0lx₂ >= 0

x1,x2 >=0

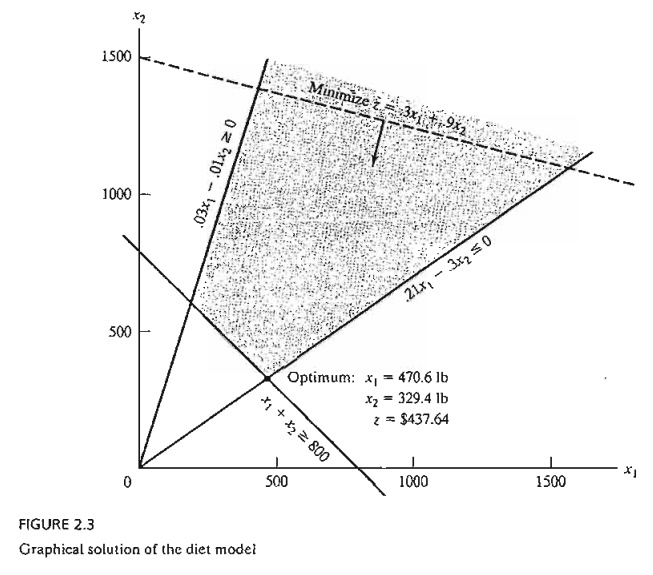
Figure 2.3 provides the graphical solution of the model. Unlike those of the Reddy Mikks model (Example 2.2-1), the second and third constraints pass through the origin. To plot the associated straight lines, we need one additional point, which can be obtained by assigning a value to one of the variables and then solving for the other variable. For example, in the second constraint, x₁ = 200 will yield .21 x 200 - .3x₂ = 0, or x₂ = 140. This means that the straight line .21x₁ - .3x2 = 0 passes through (0,0) and (200,140). Note also that (0,0) cannot be used as a reference point for constraints 2 and 3, because both lines pass through the origin. In-stead, any other point [e.g., (100, 0) or (0,100)] can be used for that purpose.

Solution:

Because the present model seeks the minimization of the objective function, we need to reduce the value of z as much as possible in the direction shown in Figure 2.3. The optimum solution is the intersection of the two lines x₁ + x₂ = 800 and .21x₁ - .3X₂ = 0, which yields X₁ = 470.591b and X₂ = 329.41 lb. The associated minimum cost of the feed mix is z = .3 X 470.59 + .9 x 329.42 = $437.65 per day.

Remarks. We need to take note of the way the constraints of the problem are constructed. Because the model is minimizing the total cost, one may argue that the solution will seek exactly 800 tons of feed. Indeed, this is what the optimum solution given above does. Does this mean then that the first constraint can be deleted altogether simply by including the amount 800 tons

in the remaining constraints? To find the answer, we state the new protein and fiber constraints as

.09x₁ + .6x₂ ≥ 3 x  800

.02x₁ + .06x₂  ≤ 05 X  800

or

.09x₁ + .6x₂  ≥ 240

.02x₁  + .06x₂ ≤ 40

The new formulation yields the solution x₁ = 0, and x₂ = 400 lb (verify with TORA!), which does not satisfy the implied requirement fOT SOO Ib of feed. This means that the constraint x₁ +x₂  ≥ 800 must be used explicitly and that the protein and fiber constraints must remain exactly as given originally.

Along the same line of reasoning, one may be tempted to replace x₁ + x₂  ≥ 800 with x₁ + x₂  =  800. In the present example, the two constraints yield the same answer. But in gen-eral this may not be the case. For example, suppose that the daily mix must include at least 500 lb of corn. In this case, the optimum solution will call for using 500 lb of corn and 350 Ib of soybean (verify with TORA!), which is equivalent to a daily feed mix of 500 + 350 = 850 lb. Imposing the equality constraint a priori will lead to the conclusion that the problem has no feasible solution (verify with TORA!). On the other hand, the use of the inequality is inclusive of the equality case, and hence its use does not prevent the model from producing exactly 800 Ib of feed mix, should the remaining constraints allow it. The conclusion is that we should not "pre-guess" the solution by imposing the additional equality restriction, and we should always use in-equalities unless the situation explicitly stipulates the use of equalities.

PROBLEM SET 2.2B

1. Identify the direction of decrease in z in each of the following cases:

                       Minimize z = 4x_I  - 2x₂'

                                                           Minimize z = -3x₁  + x₂'

                                                           Minimize z = - x₁  -   2x₂'

2. For the diet model, suppose that the daily availability of corn is limited to 450 lb. Identify the new solution space, and determine the new optimum solution.

3. For the diet model, what type of optimum solution would the model yield if the feed mix should not exceed 800 Ib a day? Does the solution make sense?

4. John must work at least 20 hours a week to supplement his income while attending school. He has the opportunity to work in two retail stores. In store 1, he can work between 5 and 12 hours a week, and in store 2 he is allowed between 6 and 10 hours. Both stores pay the same hourly wage. In deciding how many hours to work in each store, John wants to base his decision on work stress. Based on interviews with present employees, John estimates that, on an ascending scale of 1 to 10, the stress factors are 8 and 6 at stores 1 and 2, respectively. Because stress mounts by the hour, he assumes that the total stress for each store at the end of the week is proportional to the number of hours he works in the store. How many hours should 10hn work in each store?

5. OilCo is building a refinery to produce four products: diesel, gasoline, lubricants, and jet fuel. The minimum demand (in bbl/day) for each of these products is 14,000,30,000, 10,000, and 8,000, respectively. Iran and Dubai are under contract to ship crude to OilCo. Because of the production quotas specified by OPEC (Organization of Petroleum Ex-porting Countries) the new refinery can receive at least 40% of its crude from Iran and the remaining amount from Dubai. OilCo predicts that the demand and crude oil quotas will remain steady over the next ten years.

The specifications of the two crude oils lead to different product mixes: One barrel of Iran crude yields .2 bbl of diesel, .25 bbl of gasoline,. l bbl of lubricant, and .15 bbl of jet fuel. The corresponding yields from Dubai crude are .1, .6, .15, and .1, respectively.

Oileo needs to determine the minimum capacity of the refinery (in bbll day).

6. Day Trader wants to invest a sum of money that would generate an annual yield of at least $10,000. Two stock groups are available: blue chips and high tech, with average an-nual yields of 10% and 25%, respectively. Though high-tech stocks provide higher yield, they are more risky, and Trader wants to limit the amount invested in these stocks to no more than 60% of the total investment. What is the minimum amount Trader should in-vest in each stock group to accomplish the investment goal?

7. An industrial recycling center uses two scrap aluminum metals, A and B, to produce a special alloy. Scrap A contains 6% aluminum, 3% silicon, and 4 % carbon. Scrap B has 3% aluminum, 6% silicon, and 3% carbon. The costs per ton for scraps A and Bare $100 and $80, respectively. TIle specifications of the special alloy require that (1) the aluminum content must be at least 3% and at most 6%, (2) the silicon content must lie between 3% and 5%, and (3) the carbon content must be between 3% and 7%. Determine the opti-mum mix of the scraps that should be used in producing 1000 tons of the alloy.

8. TO RA Experiment. Consider the Diet Model and let the objective function be given as

Minimize z = .8x₁ + .8x₂

Use TORA to show that the optimum solution is associated with two distinct corner points and that both points yield the same objective value. In this case, the problem is said to have alternative optima. Explain the conditions leading to this situation and show that, in effect, the problem has an infinite number of alternative optima, then provide a formula for determining all such solutions.