Transpositions (Permutations)

Transpositions (Permutations)

The goal of substitution is confusion; the encryption method is an attempt to make it difficult for a cryptanalyst or intruder to determine how a message and key were transformed into ciphertext. In this section, we look at a different kind of scrambling with the similar goal. A transposition is an encryption in which the letters of the message are rearranged. With transposition, the cryptography aims for diffusion, widely spreading the information from the message or the key across the ciphertext. Transpositions try to break established patterns. Because a transposition is a rearrangement of the symbols of a message, it is also known as a permutation.

Columnar Transpositions

As with substitutions, we begin this study of transpositions by examining a simple example. The columnar transposition is a rearrangement of the characters of the plaintext into columns.

The following set of characters is a five-column transposition. The plaintext characters are written in rows of five and arranged one row after another, as shown here.

For instance, suppose you want to write the plaintext message THIS IS A MESSAGE TO SHOW HOW A COLUMNAR TRANSPOSITION WORKS. We arrange the letters in five columns as

The resulting ciphertext would then be read down the columns as

tssoh oaniw haaso lrsto imghw 

utpir seeoa mrook istwc nasns

In this example, the length of this message happens to be a multiple of five, so all columns are the same length. However, if the message length is not a multiple of the length of a row, the last columns will be one or more letters short. When this happens, we sometimes use an infrequent letter, such as X, to fill in any short columns.

Encipherment/Decipherment Complexity

This cipher involves no additional work beyond arranging the letters and reading them off again. Therefore, the algorithm requires a constant amount of work per character, and the time needed to apply the algorithm is proportional to the length of the message.

However, we must also consider the amount of space needed to record or store the ciphertext. So far, the other ciphers we have seen require

only a constant amount of space (admittedly up to 26² locations). But the columnar transposition algorithm requires storage for all characters of the message, so the space required is not constant; it depends directly on the length of the message.

Furthermore, we cannot produce output characters until all the message's characters have been read. This restriction occurs because all characters must be entered in the first column before output of the second column can begin, but the first column is not complete until all characters have been read. Thus, the delay associated with this algorithm also depends on the length of the message, as opposed to the constant delay we have seen in previous algorithms.

Because of the storage space needed and the delay involved in decrypting the ciphertext, this algorithm is not especially appropriate for long messages when time is of the essence.

Digrams, Trigrams, and Other Patterns

Just as there are characteristic letter frequencies, there are also characteristic patterns of pairs of adjacent letters, called digrams. Letter pairs such as -re-, -th-, -en-, and -ed - appear very frequently. Table 2-2 lists the ten most common digrams and trigrams (groups of three letters) in English. (They are shown in descending order of frequency.)

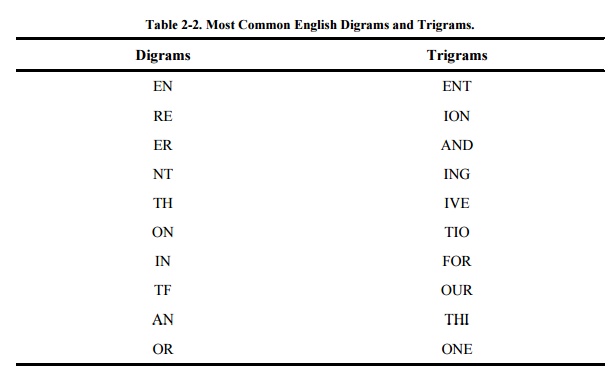
It is also useful to know which pairs and triples do not occur often in English because that information helps us eliminate possibilities when decrypting a message. For instance, digram combinations such as -vk- and -qp- occur very infrequently. (The infrequent combinations can occur in acronyms, in foreign words or names, or across word boundaries.) The frequency of appearance of letter groups can be used to match up plaintext letters that have been separated in a ciphertext.

Cryptanalysis by Digram Analysis

Suppose we want to decrypt a message that has used a columnar transposition for its encryption algorithm. The basic attack on columnar transpositions is not as precise as the attack on substitution ciphers. Even though transpositions look less secure than substitutions, they can in fact be more secure. Transpositions leave the plaintext letters intact, so the work for the cryptanalyst is more exhausting; more relies on a human's judgment of what "looks right."

The first step in analyzing the transposition is computing the letter frequencies. If we find that in fact all letters appear with their normal frequencies, we can infer that a transposition has been performed. Given a string of text, the trick then is to break it into columns.

Two different strings of letters from a transposition ciphertext can represent pairs of adjacent letters from the plaintext. The problem is to find where in the ciphertext a pair of adjacent columns lies and where the ends of the columns are.

We must do an exhaustive comparison of strings of ciphertext. The process compares a block of ciphertext characters against characters successively farther away in the ciphertext. To see how this works, imagine a moving window that locates a block of characters for checking. Assume the block being compared is seven characters. The first comparison is c₁ to c₈, c₂ to c₉, …, c₇ to c₁₄. Then, we try a distance of eight characters, and so the window of comparison shifts and c₁ is compared to c₉, c₂ to c₁₀, and continuing. For a block of nine characters, the window shifts again to c₁ against c₁₀, and so forth. This process is shown in Figure 2-5.

For each window position, we ask two questions. First, do common digrams appear, and second, do most of the digrams look reasonable? When digrams indicate a possible match for a fragment of ciphertext, the next step is to try to extend the match. The distance between c₁ and c_k+1 implies that another column might begin k positions later (because the distance is k). If c_i and c_i+k match, so also should c_i+k and c_i+2k, etc. To test that theory, we check c_k against c_2k, and so on.

Combinations of Approaches

Substitution and transposition can be considered as building blocks for encryption. Other techniques can be based on each of them, both of them, or a combination with yet another approach. For instance, Sidebar 2-5 describes how substitution can be combined with a one-time pad. Keep in mind as you read about encryption that each technique is only one piece of the larger puzzle. Just as you could have a locked car inside a locked garage, you could also combine various approaches to encryption to strengthen the overall security of your system.

A combination of two ciphers is called a product cipher. Product ciphers are typically performed one after another, as in E₂(E₁(P,k₁), k₂). Just because you apply two ciphers does not necessarily mean the result is any stronger than, or even as strong as, either individual cipher.

Sidebar 2-5: Soviet Encryption During World War II

Kahn [KAH96] describes a system that the Soviet Union thought unbreakable during World War II. It combined substitution with a one-time pad. The basic idea was to diffuse high-frequency letters by mapping them to single digits. This approach kept the length of cryptograms small and thus reduced the on-air time as the message was transmitted.

To see how the encryption worked, consider the eight most common letters of the English language: ASINTOER, arranged as in "a sin to er(r)" to make them easy to remember. These letters were assigned to single digits, 0 to 7. To encode a message, an analyst would begin by selecting a keyword that became the first row of a matrix. Then, the remaining letters of the alphabet were listed in rows underneath, as shown below. Moving vertically through the matrix, the digits 0 to 7 were assigned to the eight common letters, and then the two-digit groups from 80 to 99 were mapped to the remaining letters of the alphabet plus any symbols. In our example, the keyword is SUNDAY:

or 99983431 09344556 69361480 7423. (Digits of plaintext numbers were repeated.) Finally, the numerical message was encrypted with a one-time pad from a common reference book with numerical tablesone that would not arouse suspicion, such as a navigator's book of tables.