Substitution Ciphers

Substitution Ciphers

Children sometimes devise "secret codes" that use a correspondence table with which to substitute a character or symbol for each character of the original message. This technique is called a monoalphabetic cipher or simple substitution. A substitution is an acceptable way of encrypting text. In this section, we study several kinds of substitution ciphers.

The Caesar Cipher

The Caesar cipher has an important place in history. Julius Caesar is said to have been the first to use this scheme, in which each letter is translated to the letter a fixed number of places after it in the alphabet. Caesar used a shift of 3, so plaintext letter p_i was enciphered as ciphertext letter c_i by the rule

c_i = E(p_i) = p_i + 3

Using this encryption, the message

TREATY IMPOSSIBLE

would be encoded as

T R E A T Y I M P O S S I B L E w u h d w b l p s r v v l e o h

Advantages and Disadvantages of the Caesar Cipher

Most ciphers, and especially the early ones, had to be easy to perform in the field. In particular, it was dangerous to have the cryptosystem algorithms written down for the soldiers or spies to follow. Any cipher that was so complicated that its algorithm had to be written out was at risk of being revealed if the interceptor caught a sender with the written instructions. Then, the interceptor could readily decode any ciphertext messages intercepted (until the encryption algorithm could be changed).

The Caesar cipher is quite simple. During Caesar's lifetime, the simplicity did not dramatically compromise the safety of the encryption because anything written, even in plaintext, was rather well protected; few people knew how to read! The pattern p_i + 3 was easy to memorize and implement. A sender in the field could write out a plaintext and a ciphertext alphabet, encode a message to be sent, and then destroy the paper containing the alphabets. Sidebar 2-3 describes actual use of a cipher similar to the Caesar cipher.

Sidebar 2-3: Mafia Boss Uses Encryption

Arrested in Sicily in April 2006, the reputed head of an Italian Mafia family, Bernardo Provenzano, made notes, pizzini in the Sicilian dialect. When arrested, he left approximately 350 of the notes behind. In the pizzini he gives instructions to his lieutenants regarding particular people.

Instead of writing the name of a person, Provenzano used a variation of the Caesar cipher in which letters were replaced by numbers: A by 4, B by 5, … Z by 24 (there are only 21 letters in the Italian alphabet). So in one of his notes the string "…I met 512151522 191212154 and we agreed that we will see each other after the holidays…," refers to Binnu Riina, an associate arrested soon after Provenzano [LOR06]. Police decrypted notes found before Provenzano's arrest and used clues in them to find the boss, wanted for 40 years.

All notes appear to use the same encryption, making them trivial to decrypt once police discerned the pattern.

Suggestions we might make to Sig. Provenzano: use a strong encryption algorithm, change the encryption key from time to time, and hire a cryptographer.

Its obvious pattern is also the major weakness of the Caesar cipher. A secure encryption should not allow an interceptor to use a small piece of the ciphertext to predict the entire pattern of the encryption.

Cryptanalysis of the Caesar Cipher

Let us take a closer look at the result of applying Caesar's encryption technique to "TREATY IMPOSSIBLE." If we did not know the plaintext and were trying to guess it, we would have many clues from the ciphertext. For example, the break between the two words is preserved in the ciphertext, and double letters are preserved: The SS is translated to vv. We might also notice that when a letter is repeated, it maps again to the same ciphertext as it did previously. So the letters T, I, and E always translate to w, l, and h. These clues make this cipher easy to break.

Suppose you are given the following ciphertext message, and you want to try to determine the original plaintext.

wklv phvvdjh lv qrw wrr kdug wr euhdn

The message has actually been enciphered with a 27-symbol alphabet: A through Z plus the "blank" character or separator between words.

As a start, assume that the coder was lazy and has allowed the blank to be translated to itself. If your assumption is true, it is an exceptional piece of information; knowing where the spaces are allows us to see which are the small words. English has relatively few small words, such as am, is, to, be, he, we, and, are, you, she, and so on. Therefore, one way to attack this problem and break the encryption is to substitute known short words at appropriate places in the ciphertext until you have something that seems to be meaningful. Once the small words fall into place, you can try substituting for matching characters at other places in the ciphertext.

Look again at the ciphertext you are decrypting. There is a strong clue in the repeated r of the word wrr. You might use this text to guess at three-letter words that you know. For instance, two very common three-letter words having the pattern xyy are see and too; other less common possibilities are add, odd, and off. (Of course, there are also obscure possibilities like woo or gee, but it makes more sense to try the common cases first.) Moreover, the combination wr appears in the ciphertext, too, so you can determine whether the first two letters of the three-letter word also form a two-letter word.

For instance, if wrr is SEE , wr would have to be SE, which is unlikely. However, if wrr is TOO, wr would be TO, which is quite reasonable. Substituting T for w and O for r, the message becomes

The OT could be cot, dot, got, hot, lot, not, pot, rot, or tot; a likely choice is not. Unfortunately, q = N does not give any more clues because q appears only once in this sample.

The word lv is also the end of the word wklv , which probably starts with T . Likely two-letter words that can also end a longer word include so, is, in, etc. However, so is unlikely because the form T-SO is not recognizable; IN is ruled out because of the previous assumption that q is N. A more promising alternative is to substitute IS for lv tHRoughout, and continue to analyze the message in that way.

By now, you might notice that the ciphertext letters uncovered are just three positions away from their plaintext counterparts. You (and any experienced cryptanalyst) might try that same pattern on all the unmatched ciphertext. The completion of this decryption is left as an exercise.

The cryptanalysis described here is ad hoc, using deduction based on guesses instead of solid principles. But you can take a more methodical approach, considering which letters commonly start words, which letters commonly end words, and which prefixes and suffixes are common. Cryptanalysts have compiled lists of common prefixes, common suffixes, and words having particular patterns. (For example, sleeps is a word that follows the pattern abccda.) In the next section, we look at a different analysis technique.

Other Substitutions

In substitutions, the alphabet is scrambled, and each plaintext letter maps to a unique ciphertext letter. We can describe this technique in a more mathematical way. Formally, we say that a permutation is a reordering of the elements of a sequence. For instance, we can permute the numbers l to 10 in many ways, including the permutations π₁ = 1, 3, 5, 7, 9, 10, 8, 6, 4, 2; and π₂ = 10, 9, 8, 7, 6, 5, 4, 3, 2, 1. A permutation is a function, so we can write expressions such as π₁(3) = 5 meaning that the letter in position 3 is to be replaced by the fifth letter. If the set is the first ten letters of the alphabet, π₁(3) = 5 means that c is transformed into E.

One way to scramble an alphabet is to use a key, a word that controls the permutation. For instance, if the key is word, the sender or receiver first writes the alphabet and then writes the key under the first few letters of the alphabet.

ABCDEFGHIJKLMNOPQRSTUVWXYZ word

The sender or receiver then fills in the remaining letters of the alphabet, in some easy-to-remember order, after the keyword.

ABCDEFGHIJKLMNOPQRSTUVWXYZ wordabcefghijklmnpqstuvxyz

In this example, the key is short, so most plaintext letters are only one or two positions off from their ciphertext equivalents. With a longer keyword, the distance is greater and less predictable, as shown below. Because π must map one plaintext letter to exactly one ciphertext letter, duplicate letters in a keyword, such as the second s and o in professional, are dropped.

ABCDEFGHIJKLMNOPQRSTUVWXYZ profesinalbcdghjkmqtuvwxyz

Notice that near the end of the alphabet replacements are rather close, and the last seven characters map to themselves. Conveniently, the last characters of the alphabet are among the least frequently used, so this vulnerability would give little help to an interceptor.

Still, since regularity helps an interceptor, it is desirable to have a less regular rearrangement of the letters. One possibility is to count by threes (or fives or sevens or nines) and rearrange the letters in that order. For example, one encryption uses a table that starts with

ABCDEFGHIJKLMNOPQRSTUVWXYZ adgj

using every third letter. At the end of the alphabet, the pattern continues mod 26, as shown below.

ABCDEFGHIJKLMNOPQRSTUVWXYZ adgjmpsvybehknqtwzcfilorux

There are many other examples of substitution ciphers. For instance, Sidebar 2-4 describes a substitution cipher called a poem code, used in the early days of World War II by British spies to keep the Germans from reading their messages.

Complexity of Substitution Encryption and Decryption

An important issue in using any cryptosystem is the time it takes to turn plaintext into ciphertext, and vice versa. Especially in the field (when encryption is used by spies or decryption is attempted by soldiers), it is essential that the scrambling and unscrambling not deter the authorized parties from completing their missions. The timing is directly related to the complexity of the encryption algorithm. For example, encryption and decryption with substitution ciphers can be performed by direct lookup in a table illustrating the correspondence, like the ones shown in our examples. Transforming a single character can be done in a constant amount of time, so we express the complexity of the algorithm by saying that the time to encrypt a message of n characters is proportional to n. One way of thinking of this expression is that if one message is twice as long as another, it will take twice as long to encrypt.

Sidebar 2-4: Poem Codes

During World War II, the British Special Operations Executive (SOE) produced codes to be used by spies in hostile territory. The SOE devised poem codes for use in encrypting and decrypting messages. For security reasons, each message had to be at least 200 letters long.

To encode a message, an agent chose five words at random from his or her poem, and then assigned a number to each letter of these words. The numbers were the basis for the encryption. To let the Home Station know which five words were chosen, the words were inserted at the beginning of the message. However, using familiar poems created a huge vulnerability. For example, if the German agents knew the British national anthem, then they might guess the poem from fewer than five words. As Marks explains, if the words included "'our,' 'gracious,' 'him,' 'victorious,' 'send,' then God save the agent" [MAR98].

For this reason, Leo Marks' job at SOE was to devise original poems so that "no reference books would be of the slightest help" in tracing the poems and the messages.

Cryptanalysis of Substitution Ciphers

The techniques described for breaking the Caesar cipher can also be used on other substitution ciphers. Short words, words with repeated patterns, and common initial and final letters all give clues for guessing the permutation.

Of course, breaking the code is a lot like working a crossword puzzle: You try a guess and continue to work to substantiate that guess until you have all the words in place or until you reach a contradiction. For a long message, this process can be extremely tedious. Fortunately, there are other approaches to breaking an encryption. In fact, analysts apply every technique at their disposal, using a combination of guess, strategy, and mathematical skill.

Cryptanalysts may attempt to decipher a particular message at hand, or they may try to determine the encryption algorithm that generated the ciphertext in the first place (so that future messages can be broken easily). One approach is to try to reverse the difficulty introduced by the encryption.

To see why, consider the difficulty of breaking a substitution cipher. At face value, such encryption techniques seem secure because there are 26! possible different encipherments. We know this because we have 26 choices of letter to substitute for the a, then 25 (all but the one chosen for a) for b, 24 (all but the ones chosen for a and b) for c, and so on, to yield 26 * 25 * 24 *…* 2 * 1 = 26! possibilities. By using a brute force attack, the cryptanalyst could try all 26! permutations of a particular ciphertext message. Working at one permutation per microsecond (assuming the cryptanalyst had the patience to review the probable-looking plaintexts produced by some of the permutations), it would still take over a thousand years to test all 26! possibilities.

We can use our knowledge of language to simplify this problem. For example, in English, some letters are used more often than others. The letters E, T, O, and A occur far more often than J, Q, X, and Z, for example. Thus, the frequency with which certain letters are used can help us to break the code more quickly. We can also recognize that the nature and context of the text being analyzed affect the distribution. For instance, in a medical article in which the term x-ray was used often, the letter x would have an uncommonly high frequency.

When messages are long enough, the frequency distribution analysis quickly betrays many of the letters of the plaintext. In this and other ways, a good cryptanalyst finds approaches for bypassing hard problems. An encryption based on a hard problem is not secure just because of the difficulty of the problem.

How difficult is it to break substitutions? With a little help from frequency distributions and letter patterns, you can probably break a substitution cipher by hand. It follows that, with the aid of computer programs and with an adequate amount of ciphertext, a good cryptanalyst can break such a cipher in an hour. Even an untrained but diligent interceptor could probably determine the plaintext in a day or so. Nevertheless, in some applications, the prospect of one day's effort, or even the appearance of a sheet full of text that makes no sense, may be enough to protect the message. Encryption, even in a simple form, will deter the casual observer.

The Cryptographer's Dilemma

As with many analysis techniques, having very little ciphertext inhibits the effectiveness of a technique being used to break an encryption. A cryptanalyst works by finding patterns. Short messages give the cryptanalyst little to work with, so short messages are fairly secure with even simple encryption.

Substitutions highlight the cryptologist's dilemma: An encryption algorithm must be regular for it to be algorithmic and for cryptographers to be able to remember it. Unfortunately, the regularity gives clues to the cryptanalyst.

There is no solution to this dilemma. In fact, cryptography and cryptanalysis at times seem to go together like a dog chasing its tail. First, the cryptographer invents a new encryption algorithm to protect a message. Then, the cryptanalyst studies the algorithm, finding its patterns and weaknesses. The cryptographer then sets out to try to secure messages by inventing a new algorithm, and then the cryptanalyst has a go at it. It is here that the principle of timeliness from Chapter 1 applies; a security measure must be strong enough to keep out the attacker only for the life of the data. Data with a short time value can be protected with simple measures.

One-Time Pads

A one-time pad is sometimes considered the perfect cipher. The name comes from an encryption method in which a large, nonrepeating set of keys is written on sheets of paper, glued together into a pad. For example, if the keys are 20 characters long and a sender must transmit a message 300 characters in length, the sender would tear off the next 15 pages of keys. The sender would write the keys one at a time above the letters of the plaintext and encipher the plaintext with a prearranged chart (called a Vigenère tableau) that has all 26 letters in each column, in some scrambled order. The sender would then destroy the used keys.

For the encryption to work, the receiver needs a pad identical to that of the sender. Upon receiving a message, the receiver takes the appropriate number of keys and deciphers the message as if it were a plain substitution with a long key. Essentially, this algorithm gives the effect of a key as long as the number of characters in the pad.

The one-time pad method has two problems: the need for absolute synchronization between sender and receiver, and the need for an unlimited number of keys. Although generating a large number of random keys is no problem, printing, distributing, storing, and accounting for such keys are problems.

Long Random Number Sequences

A close approximation of a one-time pad for use on computers is a random number generator. In fact, computer random numbers are not random; they really form a sequence with a very long period (that is, they go for a long time before repeating the sequence). In practice, a generator with a long period can be acceptable for a limited amount of time or plaintext.

To use a random number generator, the sender with a 300-character message would interrogate the computer for the next 300 random numbers, scale them to lie between 0 and 25, and use one number to encipher each character of the plaintext message.

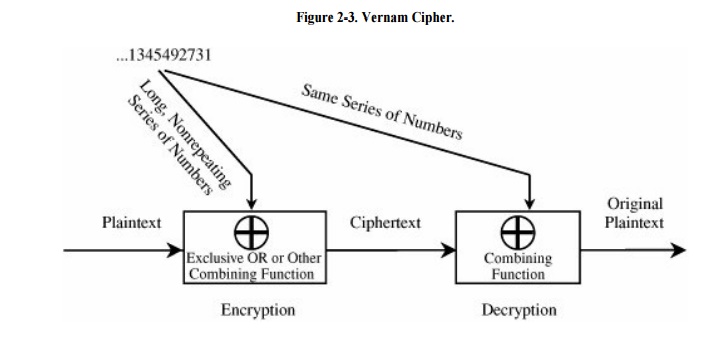
The Vernam Cipher

The Vernam cipher is a type of one-time pad devised by Gilbert Vernam for AT&T. The Vernam cipher is immune to most cryptanalytic attacks. The basic encryption involves an arbitrarily long nonrepeating sequence of numbers that are combined with the plaintext. Vernam's invention used an arbitrarily long punched paper tape that fed into a teletype machine. The tape contained random numbers that were combined with characters typed into the teletype. The sequence of random numbers had no repeats, and each tape was used only once. As long as the key tape does not repeat or is not reused, this type of cipher is immune to cryptanalytic attack because the available ciphertext does not display the pattern of the key. A model of this process is shown in Figure 2-3.

To see how this method works, we perform a simple Vernam encryption. Assume that the alphabetic letters correspond to their counterparts in arithmetic notation mod 26. That is, the letters are represented with numbers 0 through 25. To use the Vernam cipher, we sum this numerical representation with a stream of random two-digit numbers. For instance, if the message is

VERNAM CIPHER

the letters would first be converted to their numeric equivalents, as shown here.

Next, we generate random numbers to combine with the letter codes. Suppose the following series of random two-digit numbers is generated.

76 48 16 82 44 03 58 11 60 05 48 88

The encoded form of the message is the sum mod 26 of each coded letter with the corresponding random number. The result is then encoded in the usual base-26 alphabet representation.

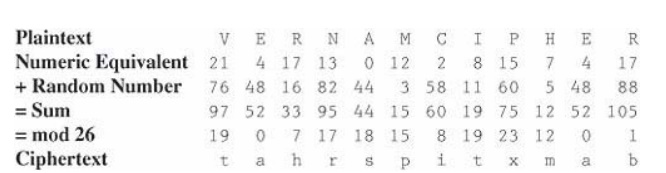
Thus, the message

VERNAM CIPHER

is encoded as

tahrsp itxmab

In this example, the repeated random number 48 happened to fall at the places of repeated letters, accounting for the repeated ciphertext letter a; such a repetition is highly unlikely. The repeated letter t comes from different plaintext letters, a much more likely occurrence. Duplicate ciphertext letters are generally unrelated when this encryption algorithm is used.

Book Ciphers

Another source of supposedly "random" numbers is any book, piece of music, or other object of which the structure can be analyzed. Both the sender and receiver need access to identical objects. For example, a possible one-time pad can be based on a telephone book. The sender and receiver might agree to start at page 35 and use two middle digits (ddd-DDdd) of each seven-digit phone number, mod 26, as a key letter for a substitution cipher. They use an already agreed-on table (a Vigenère tableau) that has all 26 letters in each column, in some scrambled order.

Any book can provide a key. The key is formed from the letters of the text, in order. This type of encryption was the basis for Ken Follett's novel, The Key to Rebecca, in which Daphne du Maurier's famous thriller acted as the source of keys for spies in World War II. Were the sender and receiver known to be using a popular book, such as The Key to Rebecca, the bible, or Security in Computing, it would be easier for the cryptanalyst to try books against the ciphertext, rather than look for patterns and use sophisticated tools.

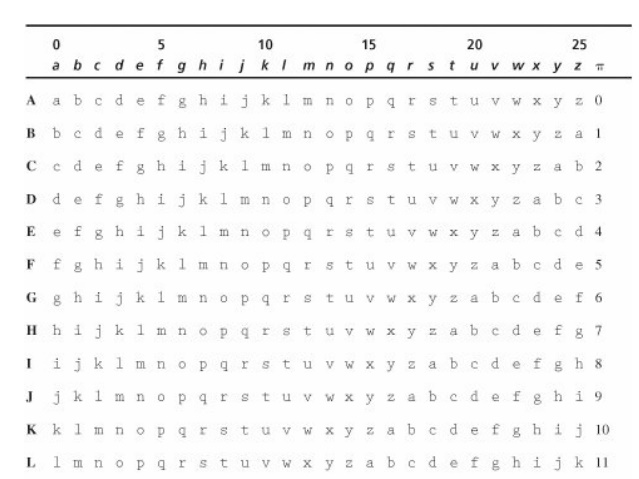
As an example of a book cipher, you might select a passage from Descarte's meditation: What of thinking? I am, I exist, that is certain. The meditation goes on for great length, certainly long enough to encipher many very long messages. To encipher the message MACHINES CANNOT THINK by using the Descartes key, you would write the message under enough of the key and encode the message by selecting the substitution in row p_i, column k_i.

iamie xistt hatis cert

MACHI NESCA NNOTT HINK

If we use the substitution table shown as Table 2-1, this message would be encrypted as uaopm kmkvt unhbl jmed because row M column i is u, row A column a is a, and so on.

It would seem as though this cipher, too, would be impossible to break. Unfortunately, that is not true. The flaw lies in the fact that neither the message nor the key text is evenly distributed; in fact, the distributions of both cluster around high -frequency letters. For example, the four letters A, E, O, and T account for approximately 40 percent of all letters used in standard English text. Each ciphertext letter is really the intersection of a plaintext letter and a key letter. But if the probability of the plaintext or the key letter's being A, E, O, or T is 0.4, the probability of both being one of the four is 0.4 * 0.4 = 0.16, or nearly one in six. Using the top six letters (adding N and I) increases the sum of the frequencies to 50 percent and thus increases the probability for a pair to 0.25, or one in four.

We look for frequent letter pairs that could have generated each ciphertext letter. The encrypted version of the message MACHINES CANNOT THINK is

uaopm kmkvt unhbl jmed

To break the cipher, assume that each letter of the ciphertext comes from a situation in which the plaintext letter (row selector) and the key letter (column selector) are both one of the six most frequent letters. (As we calculated before, this guess will be correct approximately 25 percent of the time.) The trick is to work the cipher inside out. For a ciphertext letter, look in the body of the table for the letter to appear at the intersection of one of the six rows with one of the six columns. Find combinations in the Vigenère tableau that could yield each ciphertext letter as the result of two high-frequency letters.

Searching through this table for possibilities, we transform the cryptogram.

This technique does not reveal the entire message, or even enough of it to make the message MACHI NESCA NNOTT HINK easy to identify. The technique did, however, make predictions in ten letter positions, and there was a correct prediction in seven of those ten positions. (The correct predictions are shown in bold type.) The algorithm made 20 assertions about probable letters, and eight of those 20 were correct. (A score of 8 out of 20 is 40 percent, even better than the 25 percent expected.) The algorithm does not come close to solving the cryptogram,

but it substantially reduces the 26¹⁹ possibilities for the analyst to consider. Giving this much help to the cryptanalyst is significant. A similar technique can be used even if the order of the rows is permuted.

Also, we want to stress that a one-time pad cannot repeat. If there is any repetition, the interceptor gets two streams of ciphertext: one for one block of plaintext, the other for a different plaintext, but both encrypted using the same key. The interceptor combines the two ciphertexts in such a way that the keys cancel each other out, leaving a combination of the two plaintexts. The interceptor can then do other analysis to expose patterns in the underlying plaintexts and give some likely plaintext elements. The worst case is when the user simply starts the pad over for a new message, for the interceptor may then be able to determine how to split the plaintexts and unzip the two plaintexts intact.

Summary of Substitutions

Substitutions are effective cryptographic devices. In fact, they were the basis of many cryptographic algorithms used for diplomatic communication through the first half of the twentieth century. Because they are interesting and intriguing, they show up in mysteries by Arthur Conan Doyle, Edgar Allan Poe, Agatha Christie, Ken Follett, and others.

But substitution is not the only kind of encryption technique. In the next section, we introduce the other basic cryptographic invention: the transposition (permutation). Substitutions and permutations together form a basis for some widely used commercial-grade encryption algorithms that we discuss later in this chapter.