Making "Good" Encryption Algorithms

Making "Good" Encryption Algorithms

So far, the encryption algorithms we have seen have been trivial, intended primarily to demonstrate the concepts of substitution and permutation. At the same time, we have examined several approaches cryptanalysts use to attack encryption algorithms. Now we examine algorithms that are widely used in the commercial world. Unlike the previous sections, this section does not delve deeply into the details either of the inner workings of an algorithm or its cryptanalysis. 

What Makes a "Secure" Encryption Algorithm?

There are many kinds of encryption, including many techniques beyond those we discuss in this book. Suppose you have text to encrypt. How do you choose an encryption algorithm for a particular application? To answer this question, reconsider what we have learned so far about encryption. We looked at two broad classes of algorithms: substitutions and transpositions. Substitutions "hide" the letters of the plaintext, and multiple substitutions dissipate high letter frequencies to make it harder to determine how the substitution is done. By contrast, transpositions scramble text so that adjacent-character analysis fails.

For each type of encryption we considered, we described the advantages and disadvantages. But there is a broader question: What does it mean for a cipher to be "good"? The meaning of good depends on the intended use of the cipher. A cipher to be used by military personnel in the field has different requirements from one to be used in a secure installation with substantial computer support. In this section, we look more closely at the different characteristics of ciphers.

Shannon's Characteristics of "Good" Ciphers

In 1949, Claude Shannon [SHA49] proposed several characteristics that identify a good cipher.

The amount of secrecy needed should determine the amount of labor appropriate for the encryption and decryption.

Principle 1 is a reiteration of the principle of timeliness from Chapter 1 and of the earlier observation that even a simple cipher may be strong enough to deter the casual interceptor or to hold off any interceptor for a short time.

The set of keys and the enciphering algorithm should be free from complexity.

This principle implies that we should restrict neither the choice of keys nor the types of plaintext on which the algorithm can work. For instance, an algorithm that works only on plaintext having an equal number of A's and E's is useless. Similarly, it would be difficult to select keys such that the sum of the values of the letters of the key is a prime number. Restrictions such as these make the use of the encipherment prohibitively complex. If the process is too complex, it will not be used. Furthermore, the key must be transmitted, stored, and remembered, so it must be short.

The implementation of the process should be as simple as possible.

Principle 3 was formulated with hand implementation in mind: A complicated algorithm is prone to error or likely to be forgotten. With the development and popularity of digital computers, algorithms far too complex for hand implementation became feasible. Still, the issue of complexity is important. People will avoid an encryption algorithm whose implementation process severely hinders message transmission, thereby undermining security. And a complex algorithm is more likely to be programmed incorrectly.

Errors in ciphering should not propagate and cause corruption of further information in the message.

Principle 4 acknowledges that humans make errors in their use of enciphering algorithms. One error early in the process should not throw off the entire remaining ciphertext. For example, dropping one letter in a columnar transposition throws off the entire remaining encipherment. Unless the receiver can guess where the letter was dropped, the remainder of the message will be unintelligible. By contrast, reading the wrong row or column for a polyalphabetic substitution affects only one characterremaining characters are unaffected.

The size of the enciphered text should be no larger than the text of the original message.

The idea behind principle 5 is that a ciphertext that expands dramatically in size cannot possibly carry more information than the plaintext, yet it gives the cryptanalyst more data from which to infer a pattern. Furthermore, a longer ciphertext implies more space for storage and more time to communicate.

These principles were developed before the ready availability of digital computers, even though Shannon was aware of computers and the computational power they represented. Thus, some of the concerns he expressed about hand implementation are not really limitations on computer-based implementation. For example, a cipher's implementation on a computer need not be simple, as long as the time complexity of the implementation is tolerable.

Properties of "Trustworthy" Encryption Systems

Commercial users have several requirements that must be satisfied when they select an encryption algorithm. Thus, when we say that encryption is "commercial grade," or "trustworthy," we mean that it meets these constraints:

It is based on sound mathematics. Good cryptographic algorithms are not just invented; they are derived from solid principles.

It has been analyzed by competent experts and found to be sound. Even the best cryptographic experts can think of only so many possible attacks, and the developers may become too convinced of the strength of their own algorithm. Thus, a review by critical outside experts is essential.

It has stood the "test of time." As a new algorithm gains popularity, people continue to review both its mathematical foundations and the way it builds on those foundations. Although a long period of successful use and analysis is not a guarantee of a good algorithm, the flaws in many algorithms are discovered relatively soon after their release.

Three algorithms are popular in the commercial world: DES (data encryption standard), RSA (RivestShamirAdelman, named after the inventors), and AES (advanced encryption standard). The DES and RSA algorithms (as well as others) meet our criteria for commercial-grade encryption; AES, which is rather new, meets the first two and is starting to achieve widespread adoption.

Symmetric and Asymmetric Encryption Systems

Recall that the two basic kinds of encryptions are symmetric (also called "secret key") and asymmetric (also called "public key"). Symmetric algorithms use one key, which works for both encryption and decryption. Usually, the decryption algorithm is closely related to the encryption one. (For example, the Caesar cipher with a shift of 3 uses the encryption algorithm "substitute the character three letters later in the alphabet" with the decryption "substitute the character three letters earlier in the alphabet.")

The symmetric systems provide a two-way channel to their users: A and B share a secret key, and they can both encrypt information to send to the other as well as decrypt information from the other. As long as the key remains secret, the system also provides authenticationproof that a message received was not fabricated by someone other than the declared sender. Authenticity is ensured because only the legitimate sender can produce a message that will decrypt properly with the shared key.

The symmetry of this situation is a major advantage of this type of encryption, but it also leads to a problem: key distribution. How do A and B obtain their shared secret key? And only A and B can use that key for their encrypted communications. If A wants to share encrypted communication with another user C, A and C need a different shared key. Key distribution is the major difficulty in using symmetric encryption. In general, n users who want to communicate in pairs need n * (n - 1)/2 keys. In other words, the number of keys needed increases at a rate proportional to the square of the number of users! So a property of symmetric encryption systems is that they require a means of key distribution.

Public key systems, on the other hand, excel at key management. By the nature of the public key approach, you can send a public key in an e-mail message or post it in a public directory. Only the corresponding private key, which presumably is kept private, can decrypt what has been encrypted with the public key.

But for both kinds of encryption, a key must be kept well secured. Once the symmetric or private key is known by an outsider, all messages written previously or in the future can be decrypted (and hence read or modified) by the outsider. So, for all encryption algorithms, key management is a major issue. It involves storing, safeguarding, and activating keys.

Stream and Block Ciphers

Most of the ciphers we have presented so far are stream ciphers; that is, they convert one symbol of plaintext immediately into a symbol of ciphertext. (The exception is the columnar transposition cipher.) The transformation depends only on the symbol, the key, and the control information of the encipherment algorithm. A model of stream enciphering is shown in Figure 2-6.

Some kinds of errors, such as skipping a character in the key during encryption, affect the encryption of all future characters. However, such errors can sometimes be recognized during decryption because the plaintext will be properly recovered up to a point, and then all following characters will be wrong. If that is the case, the receiver may be able to recover from the error by dropping a character of the key on the receiving end. Once the receiver has successfully recalibrated the key with the ciphertext, there will be no further effects from this error.

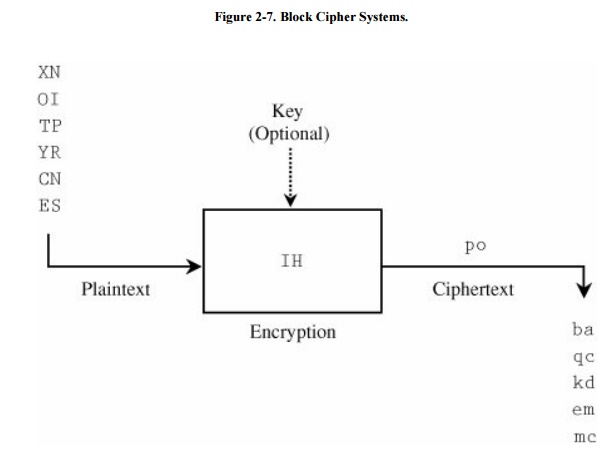
To address this problem and make it harder for a cryptanalyst to break the code, we can use block ciphers. A block cipher encrypts a group of plaintext symbols as one block. The columnar transposition and other transpositions are examples of block ciphers. In the columnar transposition, the entire message is translated as one block. The block size need not have any particular relationship to the size of a character. Block ciphers work on blocks of plaintext and produce blocks of ciphertext, as shown Figure 2-7. In the figure, the central box represents an encryption machine: The previous plaintext pair is converted to po, the current one being converted is IH, and the machine is soon to convert ES.

Confusion and Diffusion

Two additional important concepts are related to the amount of work required to perform an encryption. An encrypting algorithm should take the information from the plaintext and transform it so that the interceptor cannot readily recognize the message.

The interceptor should not be able to predict what will happen to the ciphertext by changing one character in the plaintext. We call this characteristic confusion. An algorithm providing good confusion has a complex functional relationship between the plaintext/key pair and the ciphertext. In this way, it will take an interceptor a long time to determine the relationship between plaintext, key, and ciphertext; therefore, it will take the interceptor a long time to break the code.

As an example, consider the Caesar cipher. This algorithm is not good for providing confusion because an analyst who deduces the transformation of a few letters can also predict the transformation of the remaining letters, with no additional information. By contrast, a one-time pad (with a key effectively as long as the message length) provides good confusion because one plaintext letter can be transformed to any ciphertext letter at different places in the output. There is no apparent pattern to transforming a single plaintext letter.

The cipher should also spread the information from the plaintext over the entire ciphertext so that changes in the plaintext affect many parts of the ciphertext. This principle is called diffusion, the characteristic of distributing the information from single plaintext letters over the entire output. Good diffusion means that the interceptor needs access to much of the ciphertext to be able to infer the algorithm.

Before becoming too convinced of the strength of any algorithm, you should remember that there are people very interested in defeating encryption. As we noted earlier in this chapter, the opponent can work to weaken the apparent strength of the algorithm, to decrypt a single piece encrypted text, or to derive a key with which to break subsequent encryptions. Commercial-grade cryptographers need to keep in mind the possibility of commercial-grade cryptanalysts as well.

CryptanalysisBreaking Encryption Schemes

So far we have looked at a few particular techniques a cryptanalyst could use to break the encryptions we have studied. Studying these techniques helps you appreciate the simplicity of the encryptions we have presented so far. We introduced these algorithms primarily to illustrate several encryption concepts as well as the analysis a cryptographer performs. But these techniques have been more instructional than practical; no one would use these cryptosystems to protect data of any significant value because the cryptosystems are relatively easy to break.

A different reason to consider cryptanalysis is to judge the difficulty of breaking an encryption or algorithm. After all, encrypting data does no good if the attacker can find some way of decrypting it.

Therefore, we look at cryptanalysis in general: What does a cryptanalyst do when confronted with an unknown, and possibly very strong, encryption scheme? Four possible situations confront the cryptanalyst, depending on what information is available:

ciphertext

full plaintext

partial plaintext

algorithm

In turn, these four cases suggest five different approaches the analyst can use to address them. As we describe each case, keep in mind that the cryptanalyst can also use any other collateral information that can be obtained.

Ciphertext Only

In most of the discussions so far, we assumed that the analyst had only the ciphertext with which to work. The decryption had to be based on probabilities, distributions, and characteristics of the available ciphertext, plus publicly available knowledge. This method of attack is called a ciphertext-only attack.

Full or Partial Plaintext

The analyst may be fortunate enough to have a sample message and its decipherment. For example, a diplomatic service may have intercepted an encrypted message, suspected to be the text of an official statement. If the official statement (in plaintext) is subsequently released, the interceptor has both C and P and needs only to deduce the E for which C = E(P) to find D. In this case the analyst is attempting to find E (or D) by using a known plaintext attack.

The analyst may have additional information, too. For example, the analyst may know that the message was intercepted from a diplomatic exchange between Germany and Austria. From that information, the analyst may guess that the words Bonn, Vienna, and Chancellor appear in the message. Alternatively, the message may be a memorandum to the sales force from a corporate president, and the memo would have a particular form (To: Sales Force, From: The President, Subject: Weekly Sales Update, Date: nn/nn/nn).

In these cases, the analyst can use what is called a probable plaintext analysis. After doing part of the decryption, the analyst may find places where the known message fits with the deciphered parts, thereby giving more clues about the total translation.

After cryptanalysis has provided possible partial decipherments, a probable plaintext attack may permit a cryptanalyst to fill in some blanks. For example, letter frequencies may suggest a substitution for the most popular letters, but leave gaps such as SA_ES _OR_E. With a probable plaintext, the cryptanalyst could guess that SALES FORCE appears somewhere in the memo and could easily fill in these blanks.

Ciphertext of Any Plaintext

The analyst may have infiltrated the sender's transmission process so as to be able to cause messages to be encrypted and sent at will. This attack is called a chosen plaintext attack. For instance, the analyst may be able to insert records into a database and observe the change in statistics after the insertions. Linear programming sometimes enables such an analyst to infer data that should be kept confidential in the database. Alternatively, an analyst may tap wires in a network and be able to notice the effect of sending a particular message to a particular network user. The cryptanalyst may be an insider or have an inside colleague and thus be able to cause certain transactions to be reflected in ciphertext; for example, the insider may forward messages resulting from a receipt of a large order. A chosen plaintext attack is very favorable to the analyst.

Algorithm and Ciphertext

The analyst may have available both the encryption algorithm and the ciphertext. In a chosen ciphertext attack, the analyst can run the algorithm on massive amounts of plaintext to find one plaintext message that encrypts as the ciphertext. The purpose of a chosen ciphertext attack is to deduce the sender's encryption key so as to be able to decrypt future messages by simply applying the sender's decryption key to intercepted ciphertext. This approach fails if two or more distinct keys can produce the same ciphertext as the result of encrypting (different) meaningful plaintext.

Ciphertext and Plaintext

The cryptanalyst may be lucky enough to have some pairs of plaintext and matching ciphertext. Then, the game is to deduce the key by which those pairs were encrypted so that the same key can be used in cases in which the analyst has only the ciphertext. Although it might seem uncommon to be able to obtain matching plain- and ciphertext, in fact it happens sometimes. For example, during World War II, cryptanalysts intercepted text from major diplomatic announcements sent in advance to embassies (encrypted) and then released to the public. Having a few such pieces allowed the cryptanalysts to determine current keys and decrypt other messages.

Weaknesses

A cryptanalyst works against humans, who can be hurried, lazy, careless, naïve, or uninformed. Humans sometimes fail to change cryptographic keys when needed, broadcast cryptographic keys in the clear, or choose keys in a predictable manner. That is, the algorithm may be strong and the implementation effective, but the people using it fail in some way and open up the encryption to detection. People have been known to be careless, discarding sensitive material that could give a spy access to plaintext by matching known ciphertext. And humans can sometimes be bribed or coerced. Sidebar 2-6 describes some examples of this behavior during World War II.

Sidebar 2-6: Human Fallibility Led to Cracked Codes

Kahn [KAH96] describes the history of the Enigma machine, a mechanical tool used by the Germans in World War II to scramble messages and prevent the enemy from understanding them. Enigma was based on revolving wheels, or rotors, that were wired together and connected to a typewriter keyboard. There were so many ways to encrypt a message that even if 1,000 analysts tried four different ways each minute, all day, every day, it would have taken the team 1.8 billion years to test them all.

So how did the Allies break the encryption? First, they made use of the likely chatter over the wires about each day's events. By guessing that the Germans would be discussing certain places or issues, the Allies found sections of scrambled text that they could relate to the original messages, or cleartext. Next, they concentrated on Luftwaffe messages. Counting on the likelihood that the Luftwaffe signalmen were not as well trained as those in the Army or Navy, the Allies watched for slip-ups that increased the odds of understanding the encrypted messages. For instance, Luftwaffe signalmen often used "a girlfriend's name for a key setting or beginning a second message with the same setting as that left at the ending of the first." Such knowledge enabled the Allies to determine some of the Luftwaffe's plans during the Battle of Britain. Thus, sophisticated technology can be trumped when control protocols are not followed carefully and completely.

Not only are people fallible, but so are hardware and software implementations. Sometimes hardware fails in predictable ways, such as when disk reading heads lose their track alignment, and sensitive data thought to be erased are still on the disk. At other times, seemingly small things can weaken an otherwise strong approach. For example, in one attack, the analyst accurately measured the electricity being used by a computer performing an encryption and deduced the key from the difference in power used to compute a 1 versus a 0.

These problems are separate from issues of the algorithm itself, but they offer ways that a cryptanalyst can approach the task of breaking the code. Remember that the only rule that applies to the attacker is that there are no rules.

This background information has readied you to study the three most widely used encryption schemes today: DES, AES, and RSA. Using these schemes is fairly easy, even though the detailed construction of the algorithms can be quite complex. As you study the three algorithms, keep in mind the possibility that cryptanalysts are also working to defeat these encryptions.