Elementary Cryptography - Terminology and Background

Terminology and Background

Consider the steps involved in sending messages from a sender, S, to a recipient, R. If S entrusts the message to T, who then delivers it to R, T then becomes the transmission medium. If an outsider, O, wants to access the message (to read, change, or even destroy it), we call O an interceptor or intruder. Any time after S transmits it via T, the message is vulnerable to exploitation, and O might try to access the message in any of the following ways:

Block it, by preventing its reaching R, thereby affecting the availability of the message.

Intercept it, by reading or listening to the message, thereby affecting the confidentiality of the message.

Modify it, by seizing the message and changing it in some way, affecting the message's integrity.

Fabricate an authentic-looking message, arranging for it to be delivered as if it came from S, thereby also affecting the integrity of the message.

As you can see, a message's vulnerabilities reflect the four possible security failures we identified in Chapter 1. Fortunately, encryption is a technique that can address all these problems. Encryption, probably the most fundamental building block of secure computing, is a means of maintaining secure data in an insecure environment. (It is not the only building block, however.) In this book, we study encryption as a security technique, and we see how it is used in protecting programs, databases, networks, and electronic communications.

Terminology

Encryption is the process of encoding a message so that its meaning is not obvious; decryption is the reverse process, transforming an encrypted message back into its normal, original form. Alternatively, the terms encode and decode or encipher and decipher are used

instead of encrypt and decrypt.That is, we say that we encode, encrypt, or encipher the original message to hide its meaning. Then, we decode, decrypt, or decipher it to reveal the original message. A system for encryption and decryption is called a cryptosystem.

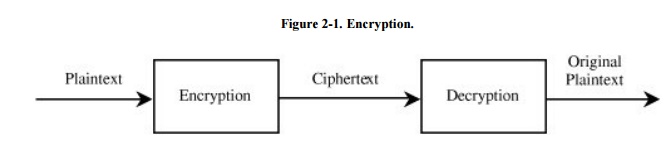
The original form of a message is known as plaintext, and the encrypted form is called ciphertext. This relationship is shown in Figure 2-1. For convenience, we denote a plaintext message P as a sequence of individual characters P = <p₁, p₂, …, p_n>. Similarly, ciphertext is

written as C = <c₁, c₂, …, c_m>. For instance, the plaintext message "I want cookies" can be denoted as the message string <I, ,w,a,n,t, , c,o,o,k,i,e,s>. It can be transformed into ciphertext <c₁, c₂, …, c₁₄>, and the encryption algorithm tells us how the transformation is done.

We use this formal notation to describe the transformations between plaintext and ciphertext. For example, we write C = E(P) and P = D (C), where C represents the ciphertext, E is the encryption rule, P is the plaintext, and D is the decryption rule. What we seek is a cryptosystem for which P = D(E(P)). In other words, we want to be able to convert the message to protect it from an intruder, but we also want to be able to get the original message back so that the receiver can read it properly.

Encryption Algorithms

The cryptosystem involves a set of rules for how to encrypt the plaintext and how to decrypt the ciphertext. The encryption and decryption rules, called algorithms , often use a device called a key, denoted by K, so that the resulting ciphertext depends on the original plaintext message, the algorithm, and the key value. We write this dependence as C = E(K, P). Essentially, E is a set of encryption algorithms, and the key K selects one specific algorithm from the set. We see later in this chapter that a cryptosystem, such as the Caesar cipher, is keyless but that keyed encryptions are more difficult to break.

This process is similar to using mass-produced locks in houses. As a homeowner, it would be very expensive for you to contract with someone to invent and make a lock just for your house. In addition, you would not know whether a particular inventor's lock was really solid or how it compared with those of other inventors. A better solution is to have a few well -known, well-respected companies producing standard locks that differ according to the (physical) key. Then, you and your neighbor might have the same model of lock, but your key will open only your lock. In the same way, it is useful to have a few well-examined encryption algorithms that everyone could use, but the differing keys would prevent someone from breaking into what you are trying to protect.

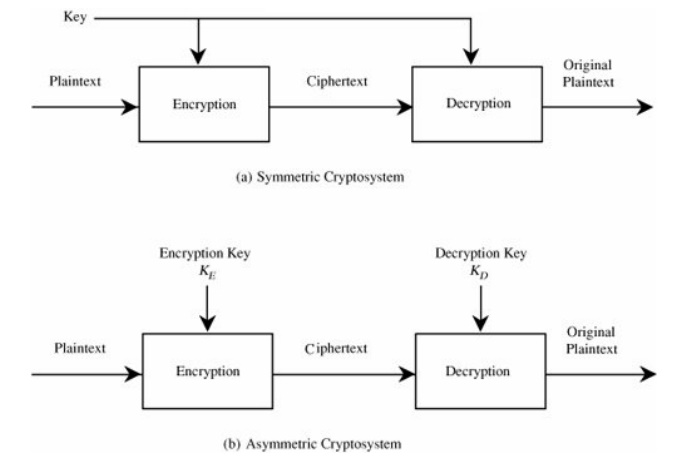
Sometimes the encryption and decryption keys are the same, so P = D(K, E(K,P)). This form is called symmetric encryption because D and E are mirror-image processes. At other times, encryption and decryption keys come in pairs. Then, a decryption key, K_D, inverts the

encryption of key K_E so that P = D(K_D, E(K_E,P)). Encryption algorithms of this form are called asymmetric because converting C back to

P involves a series of steps and a key that are different from the steps and key of E. The difference between symmetric and asymmetric encryption is shown in Figure 2-2.

A key gives us flexibility in using an encryption scheme. We can create different encryptions of one plaintext message just by changing the key. Moreover, using a key provides additional security. If the encryption algorithm should fall into the interceptor's hands, future messages can still be kept secret because the interceptor will not know the key value. Sidebar 2 -1 describes how the British dealt with written keys and codes in World War II. An encryption scheme that does not require the use of a key is called a keyless cipher.

The history of encryption is fascinating; it is well documented in Kahn's book [KAH96]. Encryption has been used for centuries to protect diplomatic and military communications, sometimes without full success. The word cryptography means hidden writing, and it refers to the practice of using encryption to conceal text. A cryptanalyst studies encryption and encrypted messages, hoping to find the hidden meanings.

Both a cryptographer and a cryptanalyst attempt to translate coded material back to its original form. Normally, a cryptographer works on behalf of a legitimate sender or receiver, whereas a cryptanalyst works on behalf of an unauthorized interceptor. Finally, cryptology is the research into and study of encryption and decryption; it includes both cryptography and cryptanalysis.

Sidebar 2-1: Silken Codes

Marks [MAR98] describes the life of a code-maker in Britain during World War II. That is, the British hired Marks and others to devise codes that could be used by spies and soldiers in the field. In the early days, the encryption scheme depended on poems that were written for each spy and relied on the spy's ability to memorize and recall them correctly.

Marks reduced the risk of error by introducing a coding scheme that was printed on pieces of silk. Silk hidden under clothing could not be felt when the spy was patted down and searched. And, unlike paper, silk burns quickly and completely, so the spy could destroy the incriminating evidence, also ensuring that the enemy could not get even fragments of the valuable code. When pressed by superiors as to why the British should use valuable silk (which was already needed for war-time necessities like parachutes) for codes, Marks said that it was a choice "between silk and cyanide."

Cryptanalysis

A cryptanalyst's chore is to break an encryption. That is, the cryptanalyst attempts to deduce the original meaning of a ciphertext message. Better yet, he or she hopes to determine which decrypting algorithm matches the encrypting algorithm so that other messages encoded in the same way can be broken. For instance, suppose two countries are at war and the first country has intercepted encrypted messages of the second. Cryptanalysts of the first country want to decipher a particular message so that the first country can anticipate the movements and resources of the second. But it is even better to discover the actual decryption algorithm; then the first country can easily break the encryption of all messages sent by the second country.

Thus, a cryptanalyst can attempt to do any or all of six different things:

break a single message

recognize patterns in encrypted messages, to be able to break subsequent ones by applying a straightforward decryption algorithm

infer some meaning without even breaking the encryption, such as noticing an unusual frequency of communication or determining something by whether the communication was short or long

deduce the key, to break subsequent messages easily

find weaknesses in the implementation or environment of use of encryption

find general weaknesses in an encryption algorithm, without necessarily having intercepted any messages

In this book, we see examples of each type of activity.

An analyst works with a variety of pieces of information: encrypted messages, known encryption algorithms, intercepted plaintext, data items known or suspected to be in a ciphertext message, mathematical or statistical tools and techniques, properties of languages, computers, and plenty of ingenuity and luck. Each piece of evidence can provide a clue, and the analyst puts the clues together to try to form a larger picture of a message's meaning in the context of how the encryption is done. Remember that there are no rules. An interceptor can use any means available to tease out the meaning of the message.

Breakable Encryption

An encryption algorithm is called breakable when, given enough time and data, an analyst can determine the algorithm. However, an algorithm that is theoretically breakable may in fact be impractical to try to break. To see why, consider a 25-character message that is

expressed in just uppercase letters. A given cipher scheme may have 26²⁵ (approximately 10³⁵) possible decipherments, so the task is to select the right one out of the 26²⁵. If your computer could perform on the order of 10¹⁰ operations per second, finding this decipherment

would require on the order of 10¹⁶ seconds, or roughly 10¹¹ years. In this case, although we know that theoretically we could generate the solution, determining the deciphering algorithm by examining all possibilities can be ignored as infeasible with current technology.

Two other important issues must be addressed when considering the breakability of encryption algorithms. First, the cryptanalyst cannot be expected to try only the hard, long way. In the example just presented, the obvious decryption might require 26²⁵ machine operations, but a

more ingenious approach might require only 10¹⁵ operations. At the speed of 10 ¹⁰ operations per second, 10¹⁵ operations take slightly more than one day. The ingenious approach is certainly feasible. As we see later in this chapter, some of the algorithms we study in this book are based on known "hard" problems that take an unreasonably long time to solve. But the cryptanalyst does not necessarily have to solve the underlying problem to break the encryption of a single message. As we note in Sidebar 2-2, sloppy use of controls can reveal likely words or phrases, and an analyst can use educated guesses combined with careful analysis to generate all or most of an important message.

Sidebar 2-2: Hidden Meanings Change the Course of World War II

In the spring of 1942, the United States was fighting Japan in the Pacific. American cryptanalysts had cracked some of the Japanese naval codes, but they didn't understand the extra encoding the Japanese used to describe particular sites. A message intercepted by the United States told the Allies' officers that "AF" was to be the target of a major assault. The U.S. Navy suspected that the assault would be on Midway island, but it needed to be sure.

Commander Joseph Rochefort, head of the U.S. Navy's cryptography center at Pearl Harbor, devised a clever plan to unearth the meaning of "AF." He directed the naval group at Midway to send a message, requesting fresh water because the water distillery had been damaged. Soon, the United States intercepted a Japanese message indicating that "AF" was short of waterverifying that "AF" indeed meant Midway! [SEI01]

Second, estimates of breakability are based on current technology. An enormous advance in computing technology has occurred since 1950. Things that were infeasible in 1940 became possible by the 1950s, and every succeeding decade has brought greater improvements.

A conjecture known as "Moore's Law" asserts that the speed of processors doubles every 1.5 years, and this conjecture has been true for over two decades. It is risky to pronounce an algorithm secure just because it cannot be broken with current technology, or worse, that it has not been broken yet.

Representing Characters

We want to study ways of encrypting any computer material, whether it is written as ASCII characters, binary data, object code, or a control stream. However, to simplify the explanations, we begin with the encryption of messages written in the standard 26-letter English alphabet, A through Z.

Because this book is written in English, the explanations refer to English. However, with slight variations, the techniques are applicable to most other written languages as well.

Throughout the book, we use the convention that plaintext is written in UPPERCASE letters, and ciphertext is in lowercase letters. Because most encryption algorithms are based on mathematical transformations, they can be explained or studied more easily in mathematical form. Therefore, in this book, we switch back and forth between letters and the numeric encoding of each letter as shown here.

Thus, the letter A is represented by a zero, B by a one, and so on. This representation allows us to consider performing arithmetic on the "letters" of a message. That is, we can perform addition and subtraction on letters by adding and subtracting the corresponding code numbers. Expressions such as A + 3 = D or K - 1 = J have their natural interpretation. Arithmetic is performed as if the alphabetic table were circular. In other words, addition wraps around from one end of the table to the other so that Y + 3 = B. Thus, every result of an arithmetic operation is between 0 and 25.

There are many types of encryption. In the next two sections we look at two simple forms of encryption: substitutions, in which one letter is exchanged for another, and transpositions, in which the order of the letters is rearranged. The goals of studying these two forms are to become familiar with the concept of encryption and decryption, to learn some of the terminology and methods of cryptanalysis, and to study some of the weaknesses to which encryption is prone. Once we have mastered the simple encryption algorithms, we explore "commercial grade" algorithms used in modern computer applications.