The Data Encryption Standard(DES)

The Data Encryption Standard

The Data Encryption Standard (DES)  , a system developed for the U.S. government, was intended for use by the general public. It has been officially accepted as a cryptographic standard both in the United States and abroad. Moreover, many hardware and software systems have been designed with the DES. However, recently its adequacy has been questioned.

Background and History

In the early 1970s, the U.S. National Bureau of Standards (NBS) recognized that the general public needed a secure encryption technique for protecting sensitive information. Historically, the U.S. Department of Defense and the Department of State had had continuing interest in encryption systems; it was thought that these departments were home to the greatest expertise in cryptology. However, precisely because of the sensitive nature of the information they were encrypting, the departments could not release any of their work. Thus, the responsibility for a more public encryption technique was delegated to the NBS.

At the same time, several private vendors had developed encryption devices, using either mechanical means or programs that individuals or firms could buy to protect their sensitive communications. The difficulty with this commercial proliferation of encryption techniques was exchange: Two users with different devices could not exchange encrypted information. Furthermore, there was no independent body capable of testing the devices extensively to verify that they properly implemented their algorithms.

It soon became clear that encryption was ripe for assessment and standardization, to promote the ability of unrelated parties to exchange encrypted information and to provide a single encryption system that could be rigorously tested and publicly certified. As a result, in 1972 the NBS issued a call for proposals for producing a public encryption algorithm. The call specified desirable criteria for such an algorithm:

·      able to provide a high level of security

·      specified and easy to understand

·      publishable so that security does not depend on the secrecy of the algorithm

·      available to all users

·      adaptable for use in diverse applications

·      economical to implement in electronic devices

·      efficient to use

·      able to be validated

·      exportable

The NBS envisioned providing the encryption as a separate hardware device. To allow the algorithm to be public, NBS hoped to reveal the algorithm itself, basing the security of the system on the keys (which would be under the control of the users).

Few organizations responded to the call, so the NBS issued a second announcement in August 1974. The most promising suggestion was the Lucifer algorithm on which IBM had been working for several years. This idea had been published earlier, so the basic algorithm was already public and had been open to scrutiny and validation. Although lengthy, the algorithm was straightforward, a natural candidate for iterative implementation in a computer program. Furthermore, unlike the MerkleHellman (which we study in Chapter 12) and RSA algorithms, which use arithmetic on 500- or 1,000- digit or longer binary numbers (far larger than most machine instructions would handle as a single quantity), Lucifer used only simple logical operations on relatively small quantities. Thus, the algorithm could be implemented fairly efficiently in either hardware or software on conventional computers.

The data encryption algorithm developed by IBM for NBS was based on Lucifer, and it became known as the Data Encryption Standard, although its proper name is DEA (Data Encryption Algorithm) in the United States and DEA1 (Data Encryption Algorithm-1) in other countries. Then, NBS called on the Department of Defense through its National Security Agency (NSA) to analyze the strength of the encryption algorithm. Finally, the NBS released the algorithm for public scrutiny and discussion.

The DES was officially adopted as a U.S. federal standard in November 1976, authorized by NBS for use on all public and private sector unclassified communication. Eventually, DES was accepted as an international standard by the International Standards Organization.

Overview of the DES Algorithm

The DES algorithm is a careful and complex combination of two fundamental building blocks of encryption: substitution and transposition. The algorithm derives its strength from repeated application of these two techniques, one on top of the other, for a total of 16 cycles. The sheer complexity of tracing a single bit through 16 iterations of substitutions and transpositions has so far stopped researchers in the public from identifying more than a handful of general properties of the algorithm.

The algorithm begins by encrypting the plaintext as blocks of 64 bits. The key is 64 bits long, but in fact it can be any 56-bit number. (The extra 8 bits are often used as check digits and do not affect encryption in normal implementations.) The user can change the key at will any time there is uncertainty about the security of the old key.

The algorithm, described in substantial detail in Chapter 12, leverages the two techniques Shannon identified to conceal information: confusion and diffusion. That is, the algorithm accomplishes two things: ensuring that the output bits have no obvious relationship to the input bits and spreading the effect of one plaintext bit to other bits in the ciphertext. Substitution provides the confusion, and transposition provides the diffusion. In general, plaintext is affected by a series of cycles of a substitution then a permutation. The iterative substitutions and permutations are performed as outlined in Figure 2-8.

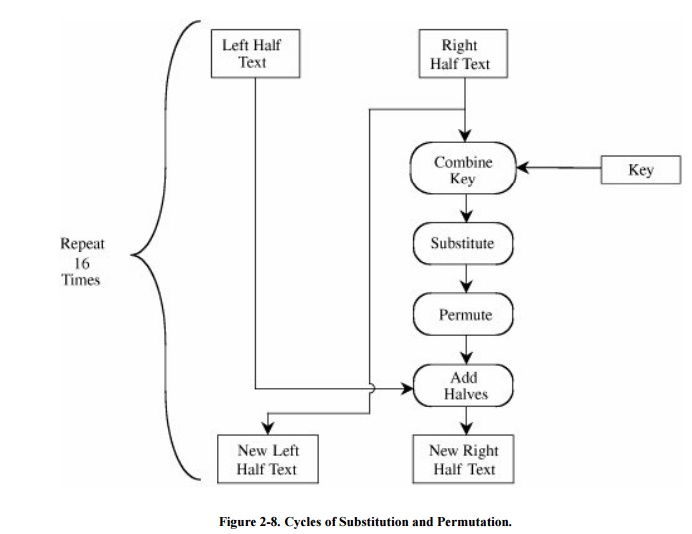
DES uses only standard arithmetic and logical operations on numbers up to 64 bits long, so it is suitable for implementation in software on most current computers. Although complex, the algorithm is repetitive, making it suitable for implementation on a single-purpose chip. In fact, several such chips are available on the market for use as basic components in devices that use DES encryption in an application.

Double and Triple DES

As you know, computing power has increased rapidly over the last few decades, and it promises to continue to do so. For this reason, the DES 56-bit key length is not long enough for some people to feel comfortable. Since the 1970s, researchers and practitioners have been interested in a longer-key version of DES. But we have a problem: The DES algorithm is fixed for a 56-bit key.

Double DES

To address the discomfort, some researchers suggest using a double encryption for greater secrecy. The double encryption works in the following way. Take two keys, k₁ and k₂, and perform two encryptions, one on top of the other: E(k₂, E(k₁,m)). In theory, this approach should multiply the difficulty of breaking the encryption, just as two locks are harder to pick than one.

Unfortunately, that assumption is false. Merkle and Hellman showed that two encryptions are no better than one. The basis of their argument is that the cryptanalyst works plaintext and ciphertext toward each other. The analyst needs two pairs of plaintext (call them P₁ and P₂) and corresponding ciphertext, C₁ and C₂, but not the keys used to encrypt them. The analyst computes and saves P₁ encrypted

under each possible key. The analyst then tries decrypting C₁ with a single key and looking for a match in the saved Ps. A match is a possible pair of double keys, so the analyst checks the match with P₂ and C₂. Computing all the Ps takes 2⁵⁶ steps, but working backward from C₁ takes only the same amount of time, for a total of 2 * 2⁵⁶ or 2⁵⁷, equivalent to a 57-bit key. Thus, the double encryption only doubles the work for the attacker. As we soon see, some 56 -bit DES keys have been derived in just days; two times days is still days, when the hope was to get months if not years for the effort of the second encryption.

Triple DES

However, a simple trick does indeed enhance the security of DES. Using three keys adds significant strength.

The so-called triple DES procedure is C = E(k₃, E(k₂, E(k₁,m))). That is, you encrypt with one key, decrypt with the second, and encrypt

with a third. This process gives a strength equivalent to a 112-bit key (because the double DES attack defeats the strength of one of the three keys).

A minor variation of triple DES, which some people also confusingly call triple DES, is C = E(k₁, D(k₂, E(k₁,m))). That is, you encrypt

with one key, decrypt with the second, and encrypt with the first again. This version requires only two keys. (The second decrypt step also makes this process work for single encryptions with one key: The decryption cancels the first encryption, so the net result is one encryption.) This approach is subject to another tricky attack, so its strength is rated at only about 80 bits.

In summary, ordinary DES has a key space of 56 bits, double DES is scarcely better, but two -key triple DES gives an effective length of 80 bits, and three-key triple DES gives a strength of 112 bits. Now, over three decades after the development of DES, a 56-bit key is inadequate for any serious confidentiality, but 80- and 112-bit effective key sizes provide reasonable security.

Security of the DES

Since its was first announced, DES has been controversial. Many researchers have questioned the security it provides. Much of this controversy has appeared in the open literature, but certain DES features have neither been revealed by the designers nor inferred by outside analysts.

In 1990, Biham and Shamir  invented a technique, differential cryptanalysis, that investigates the change in algorithmic strength when an encryption algorithm is changed in some way. In 1991 they applied their technique to DES, showing that almost any change to the algorithm weakens it. Their changes included cutting the number of iterations from 16 to 15, changing the expansion or substitution rule, or altering the order of an iteration. In each case, when they weakened the algorithm, Biham and Shamir could break the modified version.

Thus, it seems as if the design of DES is optimal.

However, Diffie and Hellman  argued in 1977 that a 56-bit key is too short. In 1977, it was prohibitive to test all 2⁵⁶ (approximately 10¹⁵) keys on then current computers. But they argued that over time, computers would become more powerful and the DES algorithm would remain unchanged; eventually, the speed of computers would exceed the strength of DES. Exactly that has happened. In 1997 researchers using over 3,500 machines in parallel were able to infer a DES key in four months' work. And in 1998 for approximately $100,000, researchers built a special "DES cracker" machine that could find a DES key in approximately four days.

Does this mean that the DES is insecure? No, not yet. No one has yet shown serious flaws in the DES. The 1997 attack required a great deal of cooperation, and the 1998 machine is rather expensive. Triple DES is still well beyond the power of these attacks. Nevertheless, to anticipate the increasing power of computers, it was clear a new, stronger algorithm was needed. In 1995, the U.S. National Institute of Standards and Technology (NIST, the renamed NBS) began the search for a new, strong encryption algorithm. The response to that search has become the Advanced Encryption Standard, or AES.