Public Key Encryption

Public Key Encryption

So far, we have looked at encryption algorithms from the point of view of making the scrambling easy to do (so that the sender can easily encrypt a message) and the decryption easy for the receiver but not for an intruder. But this functional view of transforming plaintext to ciphertext is only part of the picture. We must also examine the role of keys in encryption. We have noted how useful keys can be in deterring an intruder, but we have assumed that the key must remain secret for it to be effective. In this section, we look at ways to allow the key to be public but still protect the message. We also focus on the RSA algorithm, a public key system that is a popular commercial-grade encryption technique.

In 1976, Diffie and Hellman proposed a new kind of encryption system. With a public key encryption system, each user has a key that does not have to be kept secret. Although counterintuitive, in fact the public nature of the key does not compromise the secrecy of the system. Instead, the basis for public key encryption is to allow the key to be divulged but to keep the decryption technique secret. Public key cryptosystems accomplish this goal by using two keys: one to encrypt and the other to decrypt.

Motivation

Why should making the key public be desirable? With a conventional symmetric key system, each pair of users needs a separate key. But with public key systems, anyone using a single public key can send a secret message to a user, and the message remains adequately protected from being read by an interceptor. Let us investigate why this is so.

Recall that in general, an n-user system requires n * (n - 1)/2 keys, and each user must track and remember a key for each other user with which he or she wants to communicate. As the number of users grows, the number of keys increases very rapidly, as shown in Figure 2 -10. Determining and distributing these keys is a problem. More serious is maintaining security for the keys already distributed, because we cannot expect users to memorize so many keys.

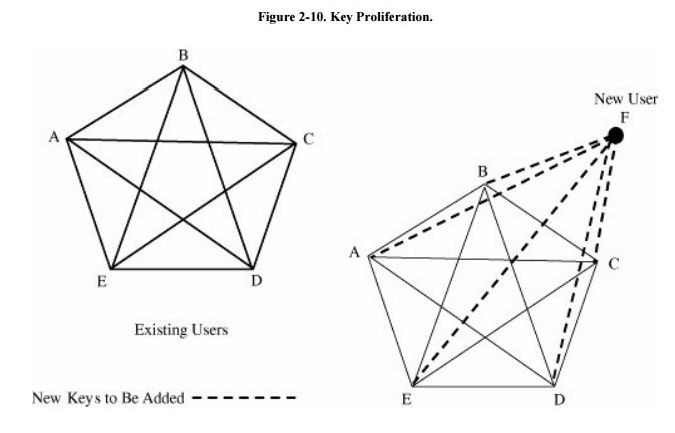
Characteristics

We can reduce the problem of key proliferation by using a public key approach. In a public key or asymmetric encryption system, each user has two keys: a public key and a private key. The user may publish the public key freely because each key does only half of the encryption and decryption process. The keys operate as inverses, meaning that one key undoes the encryption provided by the other key.

To see how, let k_PRIV be a user's private key, and let k_PUB be the corresponding public key. Then, encrypted plaintext using the public key is decrypted by application of the private key; we write the relationship as

P = D(k_PRIV, E(k_PUB, P))

That is, a user can decode with a private key what someone else has encrypted with the corresponding public key. Furthermore, with some public key encryption algorithms, including RSA, we have this relationship:

P = D(k_PUB, E(k_PRIV, P))

In other words, a user can encrypt a message with a private key, and the message can be revealed only with the corresponding public key.

These two properties tell us that public and private keys can be applied in either order. In particular, the decryption function D can be applied to any argument so that we can decrypt before we encrypt. With conventional encryption, we seldom think of decrypting before encrypting. But the concept makes sense with public keys, where it simply means applying the private transformation first and then the public one.

We have noted that a major problem with symmetric encryption is the sheer number of keys a single user has to store and track. With public keys, only two keys are needed per user: one public and one private. Let us see what difference this makes in the number of keys needed. Suppose we have three users, B, C, and D, who must pass protected messages to user A as well as to each other. Since each distinct pair of users needs a key, each user would need three different keys; for instance, A would need a key for B, a key for C, and a key for D. But using public key encryption, each of B, C, and D can encrypt messages for A by using A's public key. If B has encrypted a message using A's public key, C cannot decrypt it, even if C knew it was encrypted with A's public key. Applying A's public key twice, for example, would not decrypt the message. (We assume, of course, that A's private key remains secret.) Thus, the number of keys needed in the public key system is relatively small.

The characteristics of secret key and public key algorithms are compared in Table 2-5.

RivestShamirAdelman Encryption

The RivestShamirAdelman (RSA) cryptosystem is a public key system. Based on an underlying hard problem and named after its three inventors, this algorithm was introduced in 1978 and to date remains secure. RSA has been the subject of extensive cryptanalysis, and no serious flaws have yet been found. Although the amount of analysis is no guarantee of a method's security, our confidence in the method grows as time passes without discovery of a flaw.

Let us look at how the RSA encryption scheme works; we investigate it in greater detail in Chapter 12. RSA relies on an area of mathematics known as number theory, in which mathematicians study properties of numbers such as their prime factors. The RSA encryption algorithm combines results from number theory with the degree of difficulty in determining the prime factors of a given number. As do some of the other algorithms we have studied, the RSA algorithm also operates with arithmetic mod n.

The two keys used in RSA, d and e, are used for decryption and encryption. They are actually interchangeable: Either can be chosen as the public key, but one having been chosen, the other one must be kept private. For simplicity, we call the encryption key e and the decryption key d. Also, because of the nature of the RSA algorithm, the keys can be applied in either order:

P = E(D(P)) = D(E(P))

(You can think of E and D as two complementary functions, each of which "undoes" the other.)

 Any plaintext block P is encrypted as P^e mod n. Because the exponentiation is performed mod n, factoring P^e to uncover the encrypted plaintext is difficult. However, the decrypting key d is carefully chosen so that (P^e)^d mod n = P. Thus, the legitimate receiver who knows d simply computes (P^e)^d mod n = P and recovers P without having to factor P^e.

The encryption algorithm is based on the underlying problem of factoring large numbers. So far, nobody has found a shortcut or easy way to factor large numbers in a finite set called a field. In a highly technical but excellent paper, Boneh  reviews all the known cryptanalytic attacks on RSA and concludes that none is significant. Because the factorization problem has been open for many years, most cryptographers consider this problem a solid basis for a secure cryptosystem.