The AES Encryption Algorithm

The AES Encryption Algorithm

The AES is likely to be the commercial-grade symmetric algorithm of choice for years, if not decades. Let us look at it more closely.

The AES Contest

In January 1997, NIST called for cryptographers to develop a new encryption system. As with the call for candidates from which DES was selected, NIST made several important restrictions. The algorithms had to be

unclassified

publicly disclosed

available royalty-free for use worldwide

symmetric block cipher algorithms, for blocks of 128 bits

usable with key sizes of 128, 192, and 256 bits

In August 1998, fifteen algorithms were chosen from among those submitted; in August 1999, the field of candidates was narrowed to five finalists. The five then underwent extensive public and private scrutiny. The final selection was made on the basis not only of security but also of cost or efficiency of operation and ease of implementation in software. The winning algorithm, submitted by two Dutch cryptographers, was Rijndael (pronounced RINE dahl or, to hear the inventors pronounce it themselves, visit rijndael.com/audio/rijndael_pronunciation.wav); the algorithm's name is derived from the creators' names, Vincent Rijmen and Joan Daemen. (NIST described the four not chosen as also having adequate security for the AESno cryptographic flaws were identified in any of the five. Thus, the selection was based on efficiency and implementation characteristics.)

The AES was adopted for use by the U.S. government in December 2001 and became Federal Information Processing Standard 197 [NIS01].

Overview of Rijndael

Rijndael is a fast algorithm that can be implemented easily on simple processors. Although it has a strong mathematical foundation, it primarily uses substitution; transposition; and the shift, exclusive OR, and addition operations. Like DES, AES uses repeat cycles. There are 10, 12, or 14 cycles for keys of 128, 192, and 256 bits, respectively. In Rijndael, the cycles are called "rounds."

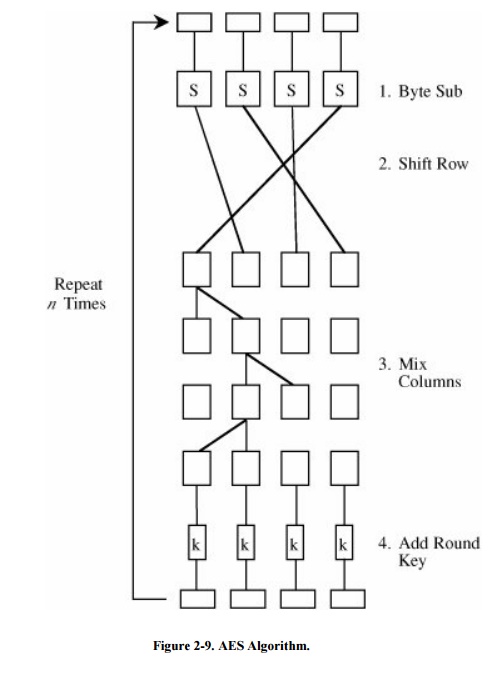
Each cycle consists of four steps.

Byte substitution: This step uses a substitution box structure similar to the DES, substituting each byte of a 128-bit block according to a substitution table. This is a straight diffusion operation.

Shift row: A transposition step. For 128- and 192-bit block sizes, row n is shifted left circular (n - 1) bytes; for 256-bit blocks, row 2 is shifted 1 byte and rows 3 and 4 are shifted 3 and 4 bytes, respectively. This is a straight confusion operation.

Mix column: This step involves shifting left and exclusive-ORing bits with themselves. These operations provide both confusion and diffusion.

Add subkey: Here, a portion of the key unique to this cycle is exclusive-ORed with the cycle result. This operation provides confusion and incorporates the key.

These four steps are described in more detail in Chapter 12. Note that the steps perform both diffusion and confusion on the input data. Bits from the key are combined with intermediate result bits frequently, so key bits are also well diffused throughout the result. Furthermore, these four steps are extremely fast. The AES algorithm is depicted in Figure 2-9.

Strength of the Algorithm

The Rijndael algorithm is quite new, so there are few reports of extensive experience with its use. However, between its submission as a candidate for AES in 1997 and its selection in 2001, it underwent extensive cryptanalysis by both government and independent cryptographers. Its Dutch inventors have no relationship to the NSA or any other part of the U.S. government, so there is no suspicion that the government somehow weakened the algorithm or added a trapdoor. Although the steps of a cycle are simple to describe and seem to be rather random transformations of bits, in fact (as described in some detail in Chapter 12), these transformations have a sound mathematical origin.

Comparison of DES and AES

When Rijndael's predecessor, DES, was adopted, two questions quickly arose:

How strong is it, and in particular, are there any backdoors?

How long would it be until the encrypted code could be routinely cracked?

With nearly 30 years of use, suspicions of weakness (intentional or not) and backdoors have pretty much been quashed. Not only have analysts failed to find any significant flaws, but in fact research has shown that seemingly insignificant changes weaken the strength of the algorithmthat is, the algorithm is the best it can be. The second question, about how long DES would last, went unanswered for a long time but then was answered very quickly by two experiments in which DES was cracked in days. Thus, after 20 years, the power of individual specialized processors and of massive parallel searches finally overtook the fixed DES key size.

We must ask the same questions about AES: Does it have flaws, and for how long will it remain sound? We cannot address the question of flaws yet, other than to say that teams of cryptanalysts pored over the design of Rijndael during the two-year review period without finding any problems.

The longevity question is more difficult, but also more optimistic, to answer for AES than for DES. The AES algorithm as defined can use 128-, 192-, or 256-bit keys. This characteristic means that AES starts with a key more than double the size of a DES key and can extend to double it yet again. (Remember that doubling the key length squares the number of possible keys that need to be tested in attempts to break the encryption.) But because there is an evident underlying structure, it is also possible to use the same general approach on a slightly different underlying problem and accommodate keys of even larger size. (Even a key size of 256 is prodigious, however.) Thus, unlike DES, AES can move to a longer key length any time technology seems to allow an analyst to overtake the current key size.

Moreover, the number of cycles can be extended in a natural way. With DES the algorithm was defined for precisely 16 cycles; to extend that number would require substantial redefinition of the algorithm. The internal structure of AES has no a priori limitation on the number of cycles. If a cryptanalyst ever concluded that 10 or 12 or 14 rounds were too low, the only change needed to improve the algorithm would be to change the limit on a repeat loop.

A mark of confidence is that the U.S. government has approved AES for protecting Secret and Top Secret classified documents. This is the first time the United States has ever approved use of a commercial algorithm derived outside the government (and furthermore outside the United States) to encrypt classified data.

However, we cannot rest on our laurels. It is impossible to predict now what limitations cryptanalysts might identify in the future. At present, AES seems to be a significant improvement over DES, and it can be improved in a natural way if necessary.