Theory Compton Effect

COMPTON EFFECT:

When a beam of monochromatic radiation such as x- rays, gamma rays etc of high frequency is allowed to fall on the scatterer, the beam is scattered into two components

i.                   One component having the same frequency or wavelength as that of the incident photon, so called unmodified radiation

ii.                 The other component having lower frequency or higher wavelength

compared to incident radiation , so called modified radiation

This effect is called Compton Effect.

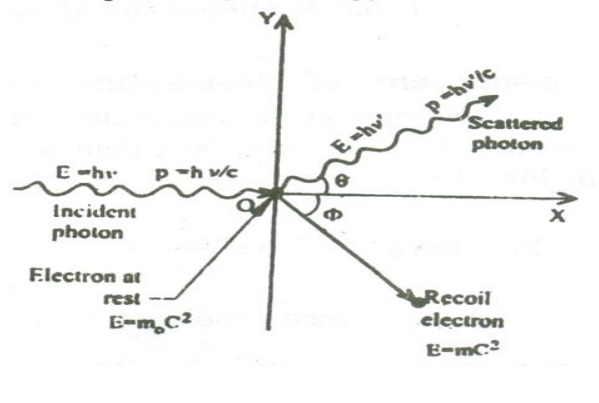
1 Compton shift:

When a photon of energy ‘hγ’ collides with an electron of a scatterer at rest; the photon gives its energy to the electron. Therefore the scattered photon will have lesser energy or lower frequency or higher wavelength compared to the wavelength of incident photon. Since the electron gains energy, it recoils with velocity’s’. This effect is called Compton Effect and the shift in wavelength is called Compton shift.

Thus as a result of Compton scattering, we get (i) unmodified radiations (ii) modified radiations and (iii) a recoil electron.

2 THEORY OF COMPTON EFFECT:

Principle:

In Compton scattering the collision between a photon and an electron is considered. Then by applying the laws if conservation of energy and momentum, the expression for Compton wavelength is derived.

Assumptions:

1.   The collision occurs between the photon and an electron in the scattering material

2. The electron is free and is at rest before collision with the incident photon.

With these assumptions, let us consider a photon energy hγ colliding within electron at rest.

During the collision process, a part of kinetic energy is given to the electron, which in turn increases the kinetic energy of the electron and hence it recoils at an angle of φ as shown.

The scattered photon moves with an energy h( lesser than hγ) , at an angle θ with respect to the original direction.

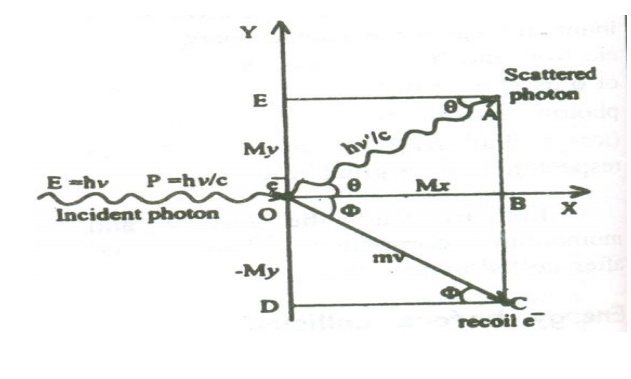
Let us find the energy and momentum components before and after collision.

ENERGY BEFORE COLLISION.

ENERGY AFTER COLLISION:

We know according to law of conservation of energy

Total energy before collision = Total energy after collision

X-component of Momentum before collision:

i.                   X-component momentum of the incident photon = ɦv/c

ii.                  X-component momentum of the electron at rest = 0

Total X-component of Momentum before collision = ɦv/c  ----- (3)

X-component of Momentum after collision:

i.            X-component of the scattered photon can be calculated from the figure.

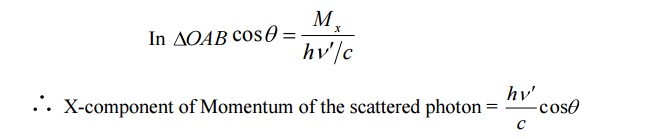
ii X-component  Momentum  of  recoil  electron  an  be  calculated  as follows

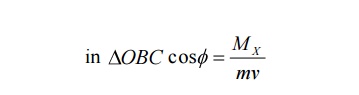
X-component Momentum of recoil electron = mv cos ϕ

Total X-component of Momentum after collision

We know according to the law of conservation of momentum

Total Momentum before collision = Total Momentum after collision

Y-component of Momentum before collision

I.            Y – component momentum of the incident photon = 0 II. Y – component of the electron at rest = 0

Total Y _component of momentum before collision = 0  - --- >> 7

Y-component of Momentum after collision

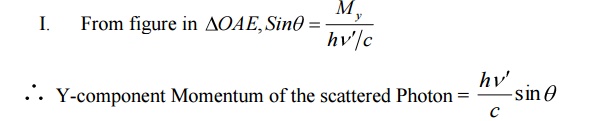
 = Y-component Momentum of the scattered Photon 

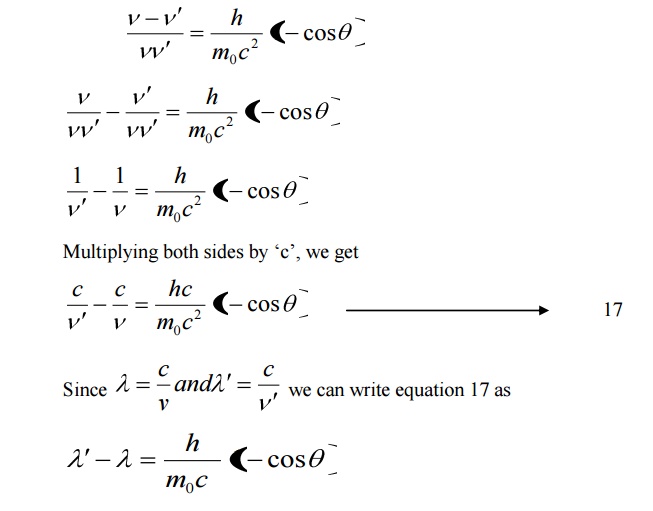
Equation 18 represents the shift in wavelength, i.e., Compton shift which is independent of the incident radiation as well as the nature of the scattering substance.

Thus the shift in wavelength or Compton shift purely depends upon the angle of scattering.

5.3 SPECIAL CASES:

Case (i) when θ = 0 cosθ = 1

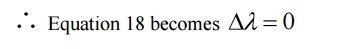
This implies that at θ = 0, the scattering is absent and the out coming radiation has the same wavelength or frequency as that of the incident radiation. Thus we get the output as a single peak.

Case (ii) when θ = 900 ;cosθ = 0

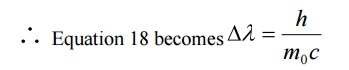
Substituting the values of h, m0, and c we have

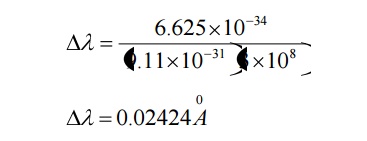
This wavelength is called Compton Wavelength, which has good agreement with the experimental results.

Case (iii) when θ = 1800 ;cosθ = 0

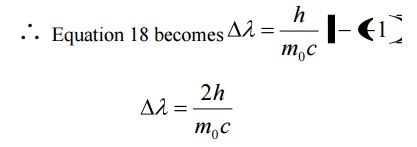
Substituting the values of h, m0, and c we have

Thus for θ =1800 the shift in wavelength is found to be maximum