Chapter: Physics : Quantum Physics
Schroedinger wave equation
SCHROEDINGER WAVE EQUATION
Schroedinger wave equation describes the wave nature of a particle in the mathematical form. It is the basic equation of motion of matter waves.
If the particle has wave properties, then there should be some sort of wave equation to describe the behavior of that particle.
Schrödinger connected the expression of de-Broglie’s wavelength with the classical wave equation for a moving particle and he obtained a new wave equation.
FORMS OF SCHROEDINGER WAVE EQUATION
There are two forms of Schröedinger wave equation. They are
a. Time independent wave equation
b. Time dependent wave equation
SCHROEDINGER TIME INDEPENDENT WAVE EQUATION
Consider a system of stationary waves associated with a particle.
Let x, y, z be the coordinates of the particle and ψ be the wave displacement for de-Broglie’s waves at any time t.
The classical differential equation of a wave motion is given by
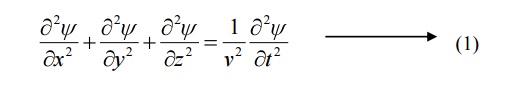
Here v is the wave velocity Equation (1) is written as




SCHROEDINGER TIME DEPENDENT WAVE EQUATION
Schoredinger time independent wave equation is derived from Schroedinger time independent wave equation.
The solution of classical differential equation of the wave motion is given by
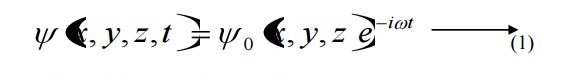
Differentiating equation (1) with respect to time t we get
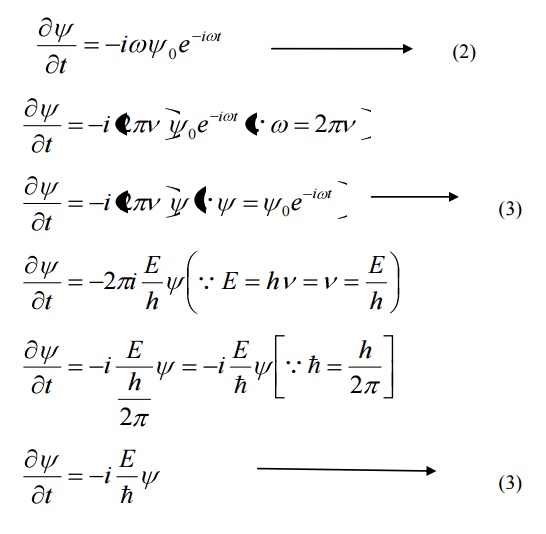
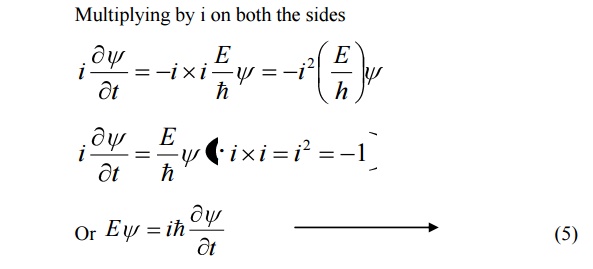
We know that Schroedinger time independent wave equation is given by

PHYSICAL SIGNIFICANCE OF WAVE FUNCTION (ψ)
1.The variable quantity that characterizes d-Broglie wave is called wave function .
2.The wave function represents the variations in the matter waves and it connects the particle nature and its associated wave nature statistically.
3.The wave function associated with a moving particle at a particular instant of time and at a particular point in space is related to the probability of finding the particle at that instant and at that point.
4. The probability 0 corresponds to the certainty of not finding the particle and probability 1 corresponds to the certainty of finding the particle.
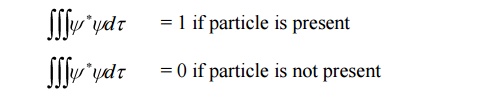
5.The wave function is a complex quantity that cannot be measured.
6.The probability of finding a particle at particular region must be real and positive, but the wave function ψ is in general a complex quantity.
The probability density is given by

PARTICLE IN A ONE DIMENSIONAL BOX
Let us consider particle (electron) of mass ’m’ moving along the x-axis, enclosed in a one dimensional potential box as shown in the figure.
Since the walls are of infinite potential the particle does not penetrate out from the box.
Also, the particle is confined between the length ‘l’ of the box and has elastic collisions with the walls. Therefore, the potential energy of the electron inside the box is constant and can be taken as zero for simplicity.

We can say that the Outside the box and on the wall of the box, the potential energy V of the electron is .
Inside the box the potential energy (V) of the electron is zero.
In other words we can write the boundary condition as

To find the wave function of the particle within the box of length ‘l’, let us consider the Schroedinger one dimensional time independent wave equation(i.e.,)

Since the potential energy inside the box is zero [i.e. =0], the particle has kinetic energy alone and thus it is named as a free particle or free electron
For a free particle (electron), the Schroedinger wave equation is given by

Equation (1) is a second order differential equation; therefore, it should have solution with two arbitrary constants.
The solution for equation (1) is given by
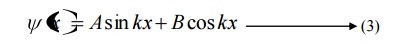
Where A and b are called Arbitrary constants, which can be found by applying the boundary conditions.

Comparing two equations, we can write kl=nπ where n is an integer.
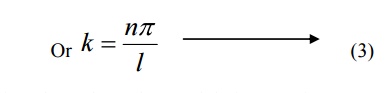
Substituting the value of B and k in equation 3 we can write the wave function associated with the free electron confined in a one dimensional box as
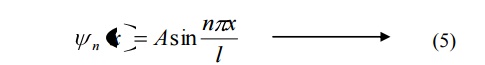
Energy of the particle(Electron)
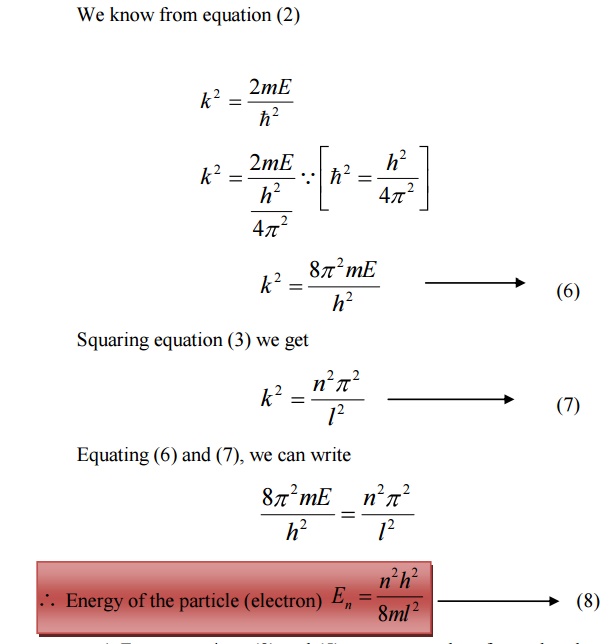
From equations (8) and (5) we can say that, for each value of ‘n’, there is an energy level and the corresponding wave function.
Thus we can say that, each value of En is known as Eigen value and the corresponding value of ψn is called Eigen function.
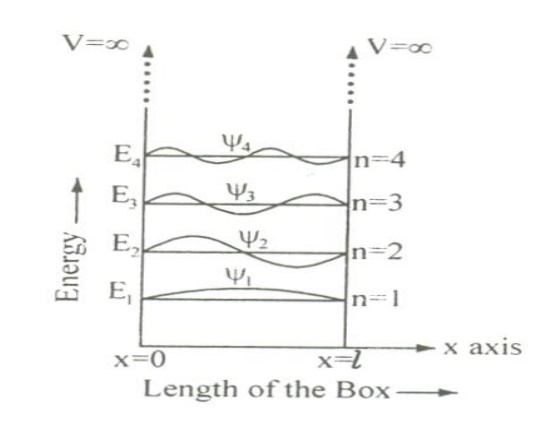
Energy levels of an electron
For various values of ‘n’ we get various energy values of the electron. The lowest energy value or ground state energy value can be got by substituting n = 1 in equation (8)

It is found that from the energy levels E1,E2,E3 etc the energy levels of an electron are discrete.
This is the great success which is achieved in Quantum Mechanics than classical mechanics, in which the energy levels are found to be continuous.
The various energy Eigen values and their corresponding Eigen functions of an electron enclosed in a one dimensional box is as shown in the figure. Thus we have discrete energy values.
Normalization of the wave function
Normalization:
It is the process by which the probability (P) of finding the particle (electron) inside the box can be done.
We know that the total probability (P) is equal to 1 means then there is a particle inside the box.
For a one dimensional potential box of length ’l’ the probability


The normalized wave function and their energy values are as shown in the figure.
The solution of one-dimensional potential box can be extended for a three dimensional potential box. In a three dimensional potential box, the particle (electron) can move in any direction in space. Therefore instead of one quantum number ‘n’ , we have to use three quantum number nx,ny, nz corresponding to the three coordinate axis x,y,z respectively
The energy of the particle = Ex + Ey+ Ez
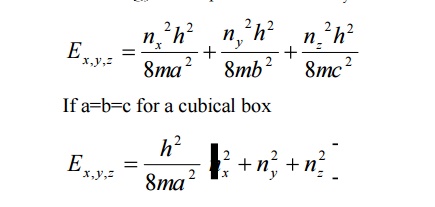
The corresponding normalized wave function of an electron in a cubical box can be written as
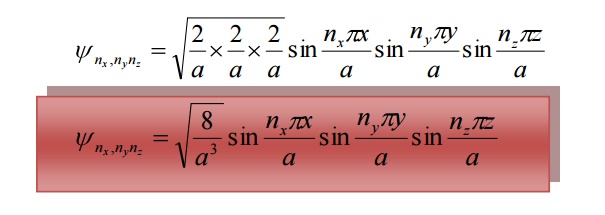
DEGENERACY AND NON-DEGENERACY
Degeneracy:
It is seen from equation (3) and equation (3), for several combination of quantum numbers we have same energy Eigen value but different Eigen functions. Such states and energy levels are called Degenerate state.
The three combinations of quantum numbers (112), (121) and (211) which gives same Eigen value but different Eigen functions are 3 fold degenerate state.
Example: nx =1 , ny =1 , nz =2
Then nx2+ny2+nz2 6
Similarly for the other two combinations also it is 6 only.

Non –degeneracy:
For various combinations of quantum number if we have same energy value and same (one) Eigen function then such states and energy levels are called Non – degenerate state.
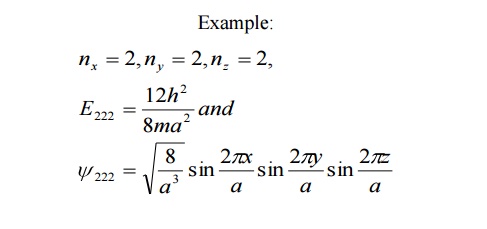
Related Topics