Chapter: Physics : Quantum Physics
Dual Nature of Radiation (Light) And Matter (Particles) - Matter Waves
DUAL NATURE OF RADIATION (LIGHT) AND MATTER (PARTICLES) – MATTER WAVES
de- Broglie concept of dual nature:
The universe is made of radiation (light) and matter (particles). The light exhibits the dual nature (ie.) it can behave both a wave (interference, diffraction, phenomenon) and as a particle (Compton Effect, photo electric effect etc.)
Since the nature loves symmetry, in 1923 Louis debroglie suggested that an electron or any other material particle must exhibit wave like properties in addition to
particle nature.
The waves associated with a material particle are called as matter waves. De-Broglie wavelength:
From the theory of light, considering a photon as a particle the total energy of the photon is given by

Where m is the mass of the particle
c is the velocity of light
Considering the photon as a wave, the total energy is given by
E = hγ ------------- > (2)
Where h is the Planck’s constant
Γ is the frequency of the radiation.
From equations (1) and (2)
E = mc2 = hγ --------- ((3))
We know Momentum = Mass × velocity
p = mc
hv=pc
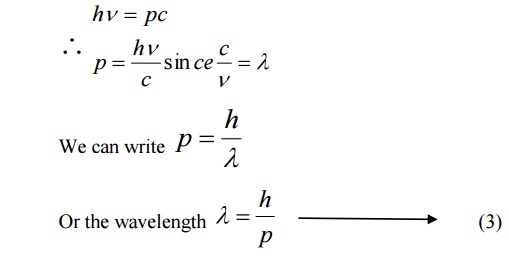
de-Broglie suggested that the equation 3 can be applied both for photons and material particles. If m is the mass of the particle and v is the velocity the particle, then
Momentum p = mv

6.1 de-Broglie wavelength in terms of energy
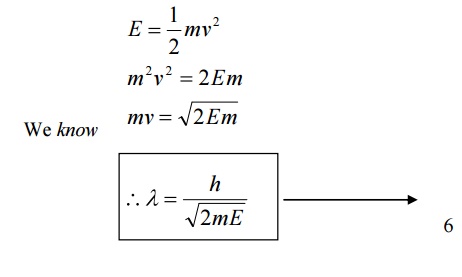
6.2 de-Broglie wavelength in terms of Voltage
If a charged particle of charge ’e’ is accelerated through a potential difference
Then the Kinetic Energy of the particle = ½ mv2 --à (7)
Also we know energy = eV -------- (8)
Equating 7 and 8, we get,
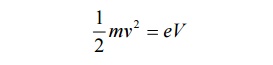
Multiplying by ‘m’ both sides, we get
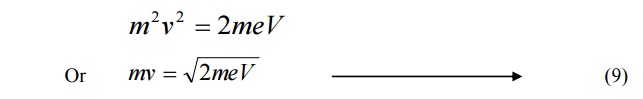
Substituting 9 in 5, we get
de-Broglie wavelength
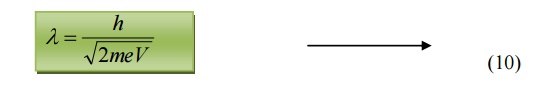
6.3 de-Broglie wavelength in terms of Temperature
When a particle like neutron is in thermal equilibrium at temperature T, then they possess Maxwell distribution of velocities.
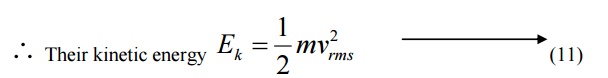
Where vrm s is the Root mean square velocity of the particle.
Also, we know energy = 
Where KB is the Boltzmann constant.
Equating (11) and (12) we get
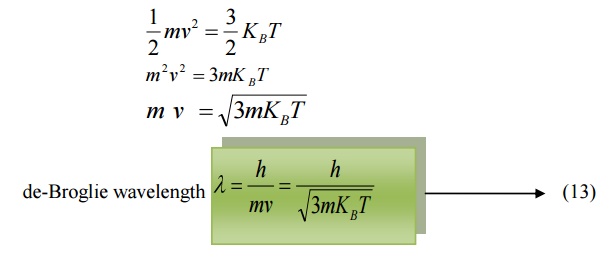
Related Topics