Black Body Radiation

BLACK BODY RADIATION:

Perfect black body:

A perfect black body is one which absorbs and emits in all the radiations (corresponding to all wavelengths) that fall on it. The radiation given out by a perfect black body is called Black body radiation.

Kirchhoff’s law:

Ratio of emissive power to the coefficient of absorption of any given wavelength is the same for all bodies at a given temperature and is equal to the emissive power of the black body at that temperature.

Experiment:

In practice a perfect black body is not available. Therefore let us consider a hollow sphere coated with lamp black on its inner surface.

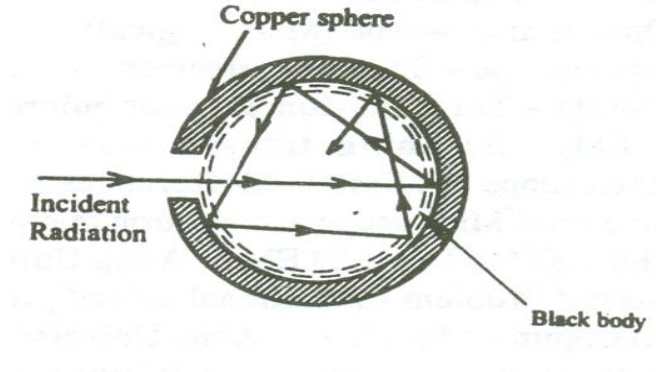
A fine hole is made for radiations to enter into the sphere as shown in the figure.

Now when the radiations are made to pass through the hole it undergoes multiple reflections and are completely absorbed. Thus the black body acts as a perfect absorber.

Now when the black body is placed in a temperature bath of fixed temperature, the heat radiations will come out only through the hole in the sphere and not through the walls of the sphere.

Therefore, we can conclude that the radiations are emitted from the inner surface of the sphere and not from the outer surface of the sphere. Thus a perfect black body is a perfect absorber and also a perfect radiator of all wavelengths.

Energy spectrum:

When a perfect black body is allowed to emit radiations at different temperatures , then the distribution of the energy for different wavelengths at various temperatures is obtained as shown in the figure.

From figure the following results are formulated.

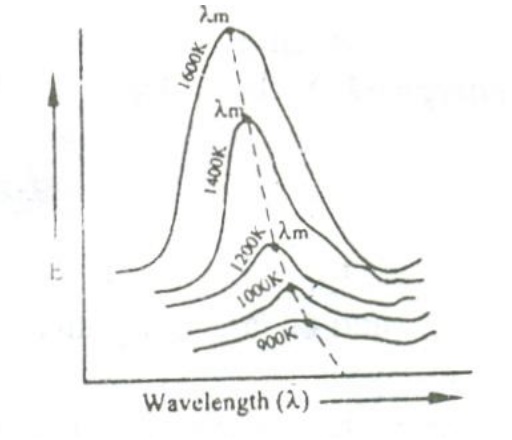
i.            The energy distribution is not uniform for a given temperature.

ii.            The intensity of radiation (E) increases with respect to the increase in wavelength at at particular wavelength in becomes maximum (λm) and after this it starts decreasing with respect to the increase in wavelength.

iii.           When the temperature is increased, the maximum wavelength (λm) decreases.

iv.            For all the wavelengths an increase in its temperature causes increase in energy.

iv.         The total energy emitted at any particular temperature can be calculated from the area under that particular curve.

Laws for explaining the energy distribution:

1. Stefan- Boltzmann Law

According to this law the radiant energy (E) of the body is directly proportional to the fourth power of the temperature (T) of the body.

2. Wien’s displacement law:

This law states that the product of then wavelength λ maximum energy and the absolute temperature (T) is a constant.

λ mT  Cons tan t

This law shows that, as the temperature increases, the wavelength corresponding to maximum energy decreases.

Wien also showed that the maximum energy (Emax) is directly proportional to the fifth power of the absolute temperature.

Em ax Dir Pro T 5

Em ax = Cons tan tT 5

By deducing this law he obtained a law called Wien’s law of distribution of energy (Eλ), given by

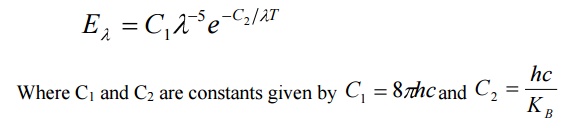
3. Raleigh Jeans law:

According to this law, the energy distribution is directly proportional to the absolute temperature and is inversely proportional to the fourth power of the wavelength.

It is governed by the equation

Where KB is Boltzmann Constant.

This law holds well only for longer wavelength regions and not for shorter wavelengths.

It is found that, both Wien’s and Raleigh Jeans law don’t agree with the experimental results. Therefore we can conclude that the classical theory was not able to explain the emission of black body radiation. Thus Max Planck used Quantum theory to explain Black body radiation.