Planck's Hypothesis

PLANCK’S HYPOTHESIS

Planck suggested that the correct results could be obtained if the energy of oscillating electrons is taken as discrete rather than continuous. He suggested quantum theory of radiation. Planck suggested in deriving the formula, which agrees extremely well with experimental results. He derived the radiation law by using the following assumptions.

a.      A black body chamber is filled up not only with radiation, but also with simple harmonic oscillators or harmonic oscillators or resonators of molecular dimensions. They can vibrate with all possible frequencies.

b.     The frequency of radiation emitted by an oscillator is the same as the frequency of its vibration.

c.      An oscillator cannot emit energy in a continuous manner. It can emit energy in the multiples of a small unit called Quantum (Photon).

If an oscillator is vibrating with a frequency γ , it can radiate in quantas of magnitude hγ . The oscillator can have only discrete energy En given by

En = n hγ    = nɛ     where hγ   = ɛ

The emission of radiation corresponds to a decrease and absorption to an increase in the energy and amplitude of an oscillator.

1 Planck’s law of radiation:  

Statement:

The energy density of heat radiation emitted from an enclosure at temperature T in the wavelength range from λ  to λ + λd is given by

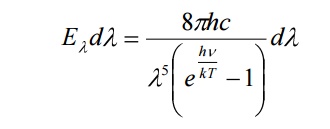
Here h = Planck’s constant

C= speed of the light

K= Boltzmann constant

T = temperature of the enclosure

2 DERIVATION OF PLANCK’S LAW OF RADIATION

Assume that a black body consists of energy by a large number of atomic oscillators.

Average energy BarE = E/N

Where E is the total energy and N is the number of oscillators.

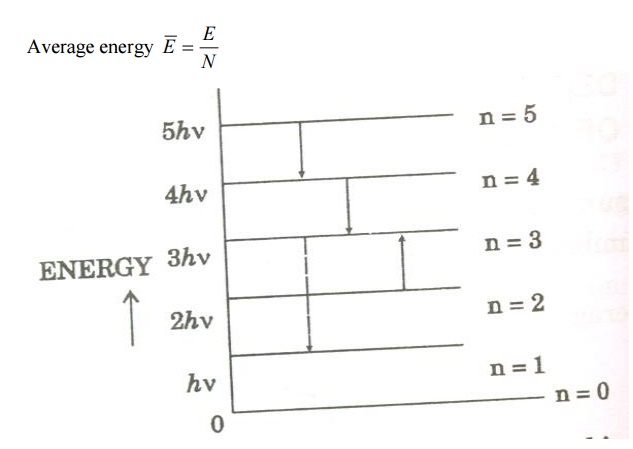
Number of atomic oscillators in ground state = N 0

From Maxwell’s distribution law, the number of oscillators having energy ɛ n in excess of ground state energy (ɛ 0 ) is given by

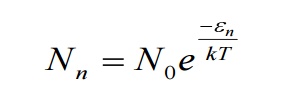
Where T – Absolute temperature

K – Boltzmann’s Constant

Let N be the total number of Planck’s oscillators and N1, N2, N3 etc be the number of oscillators with energies ɛ0 , ɛ1 , ɛ2 .......... , then

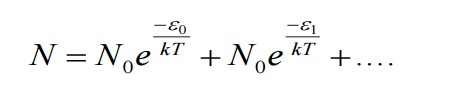
We know from Planck’s quantum theory, ɛ can be a quanta of integral values of hγ and so the possible values of ɛ are 0, 2hγ, and 3hγ etc.

Number of oscillators per unit volume in the wavelength range λ and λ+dλ is given by

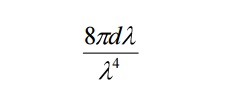
The energy density of radiation between wavelengths λ and λ+dλ is given by

Eλdλ = (Number of oscillators per unit volume in the interval λ and λ+dλ) x (Average energy per oscillator)

This equation represents Planck’s radiation law in terms of wavelength.

This law explained significantly the entire blackbody spectrum. It can also be expressed in terms of frequencies by substituting 

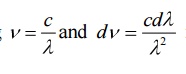
in the Planck law. Then

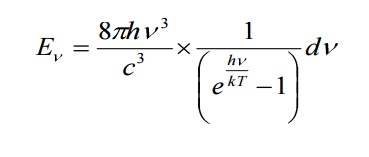
2.1 DEDUCTION OF WIEN’S DISPLACEMENT LAW:

When λ is small, γ is very large, hence 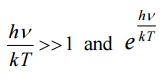 is large when compared to 1. Hence, ‘1’ is neglected in the denominator

Hence the equation reduces to

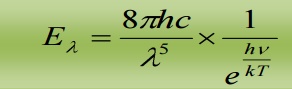
This is Wien’s displacement law.

Therefore Planck’s law reduces to Wien’s displacement for smaller wavelengths.

4.2.2 DEDUCTION OF RAYELIGH JEANS LAW:

This is Rayleigh – Jeans law.

Therefore, Planck’s law reduces to Rayleigh – Jeans law for longer

wavelength.

Planck’s formula is found to agree remarkably well with experimental observations of Lummer, Pringsheim, Kurlbaum etc. and is thus an established formula for all validity of quantum hypothesis.