The area of the region bounded by the curves: Example Solved Problems

Example 3.1

Find the area bounded by y = 4x + 3 with x- axis between the lines x = 1 and x = 4

Solution:

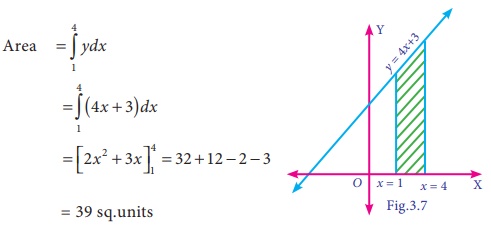
Example 3.2

Find the area of the region bounded by the line x âˆ’ 2 y âˆ’12 = 0 , the y-axis and the lines y = 2, y = 5.

Solution:

x âˆ’ 2 y âˆ’12 = 0

x = 2 y + 12

Required Area

Example 3.3

Find the area of the region bounded by the parabola y = 4 âˆ’ x2 , x âˆ’ axis and the lines x = 0, x = 2

Solutions:

Example 3.4

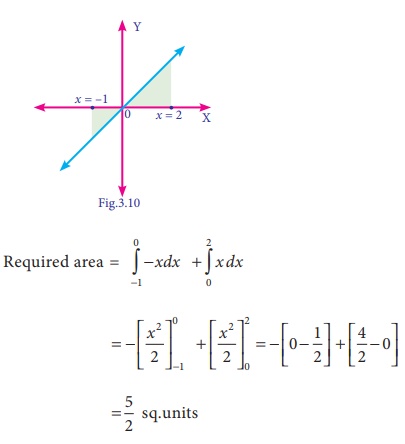
Find the area bounded by y = x between the lines x = −1and x = 2 with x -axis.

Solutions:

Example 3.5

Find the area of the parabola y 2 = 8x bounded by its latus rectum.

Solution

y2=8x           (1)

Comparing this with the standard form y 2 = 4ax ,

4a = 8

a = 2

Equation of latus rectum is x = 2

Since equation (1) is symmetrical about x- axis

Required Area = 2[Area in the first quadrant between the limits x = 0 and x = 2]

Example 3.6

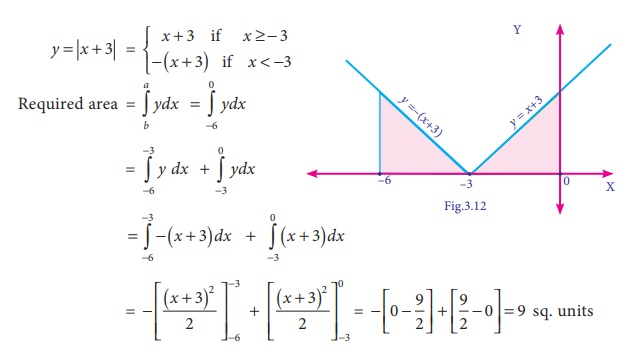
Sketch the graph y = |x + 3| and evaluate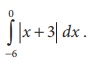 

Solution:

Example 3.7

Using integration find the area of the circle whose center is at the origin and the radius is a units.

Solution

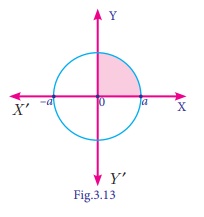
Equation of the required circle is x2 + y2 = a2               (1)

put y = 0, x2 = a2

⇒ x = ± a

Since equation (1) is symmetrical about both the axes

The required area = 4 [Area in the first quadrant between the limit 0 and a.]

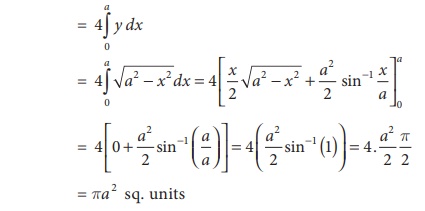
Example 3.8

Using integration find the area of the region bounded between the line x = 4 and the parabola y 2 = 16x.

Solution:

The equation y 2 = 16x represents a parabola (Open rightward)