Exercise 3.1: The area of the region bounded by the curves

Exercise 3.1

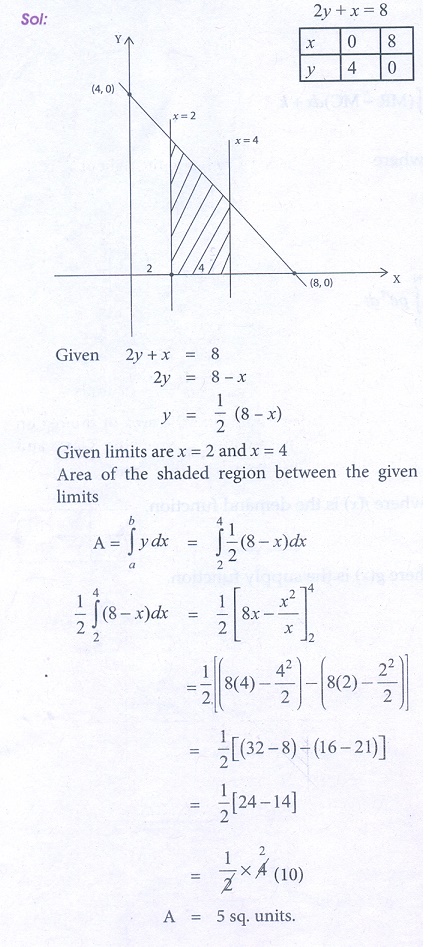
1. Using Integration, find the area of the region bounded the line 2 y + x = 8, the x axis and the lines x = 2, x = 4.

2. Find the area bounded by the lines y âˆ’ 2x âˆ’ 4 = 0, y = 1, y = 3 and the y-axis

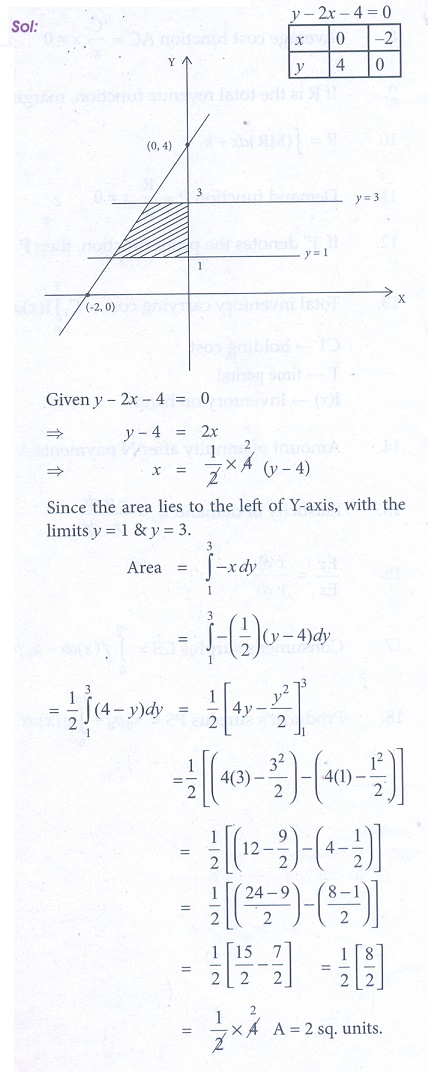
3. Calculate the area bounded by the parabola y2 = 4ax and its latusrectum.

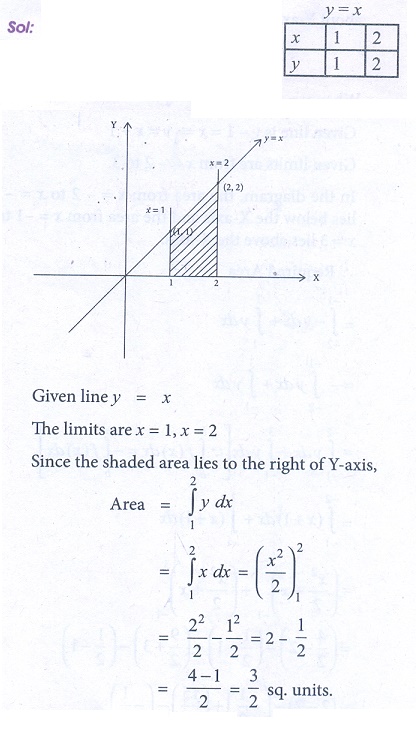
4. Find the area bounded by the line y = x, the x-axis and the ordinates x = 1, x = 2.

5. Using integration, find the area of the region bounded by the line y âˆ’ 1 = x ,the x axis and the ordinates x = –2, x = 3.

6. Find the area of the region lying in the first quadrant bounded by the region y = 4x2 , x = 0, y = 0 and y = 4.

7. Find the area bounded by the curve y = x2 and the line y = 4

Answers: