Integration: Producer surplus

Producer surplus

A supply function g(x) represents the quantity that can be supplied at a price p. Let p₀ be the market price for the corresponding supply x_o . But there can be some producers who are willing to supply the commodity below the market price gain from the fact that the price is p₀. This gain is called the producer’s surplus. It is represented in the following diagram. 

Mathematically, producer’s surplus (PS) can be defined as,

PS = (Area of the rectangle OAPB) − (Area below the supply function from x = 0 to x = x₀ )

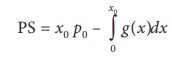
Example 3.28

Find the producer’s surplus defined by the supply curve g(x) = 4x+8 when x_o= 5.

Solution:

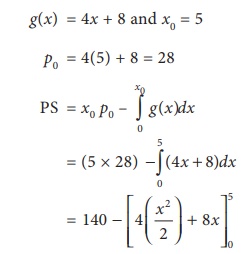
= 140 – (50 + 40)

 = 50 units

 Hence the producer’s surplus= 50 units.

Example 3.29

The demand and supply function of a commodity are p_d = 18 − 2x − x² and p_s = 2x − 3 . Find the consumer’s surplus and producer’s surplus at equilibrium price.

Solution:

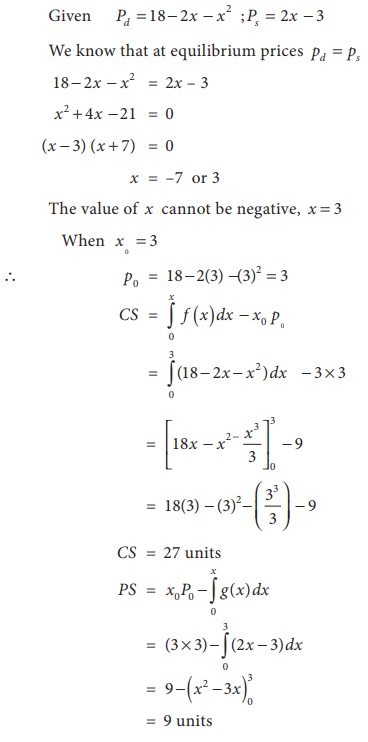
Hence at equilibrium price,

(i) the consumer’s surplus is 27 units

(ii) the producer’s surplus is 9 units.