Integration: Revenue functions from Marginal revenue functions

Revenue functions from Marginal revenue functions

If R is the total revenue function when the output is x, then marginal revenue MR = dR/dx Integrating with respect to ‘ x ’ we get

Revenue Function, R = ∫ ( MR ) dx + k.

Where ‘k’ is the constant of integration which can be evaluated under given conditions, when x = 0, the total revenue R = 0,

Demand Function, P=R/x, x ≠ 0

Example 3.16

For the marginal revenue function MR = 35 + 7x − 3x² , find the revenue function and demand function.

Solution:

Example 3.17

A firm has the marginal revenue function given by MR = 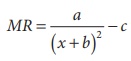 where x is the output and a, b, c are constants. Show that the demand function is given by x =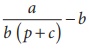 

Solution:

To find the Maximum Profit if Marginal Revenue and Marginal cost function are given:

If ‘P’ denotes the profit function, then 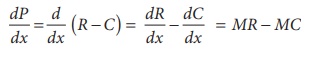 Integrating both sides with respect to x gives , P = ∫( MR − MC ) dx + k

Where k is the constant of integration. However if we are given additional information, such as fixed cost or loss at zero level of output, we can determine the constant k. Once P is known, it can be maximum by using the concept of maxima and minima.

Example 3.18

The marginal cost C ′ ( x) and marginal revenue R ′ ( x) are given by C ′ ( x) = 50 + x/50 and R′ ( x)= 60 . The fixed cost is ₹200. Determine the maximum profit.

Solution:

When quantity produced is zero, then the fixed cost is 200.

i.e. When    x = 0, c = 200

k₁ =200

=5000 – 2500 – 200

=2300

Profit = ₹ 2,300.

Example 3.19

The marginal cost and marginal revenue with respect to commodity of a firm are given by C ′ ( x) = 8 + 6x and R ′ ( x)= 24. Find the total Profit given that the total cost at zero output is zero.

Solution:

Example 3.20

The marginal revenue function (in thousand of rupees ) of a commodity is 10 + e^{−0. 05x} Where x is the number of units sold. Find the total revenue from the sale of 100 units (e^−5 = 0.0067)

Solution:

Given, Marginal revenue R ′ ( x) = 10 + e^{−0 .05x} 

Total revenue from sale of 100 units is

Total revenue = 1019.87 × 1000

= ₹10,19,870

Example 3.21

The price of a machine is ₹5,00,000 with an estimated life of 12 years. The estimated salvage value is ₹30,000. The machine can be rented at ₹72,000 per year. The present value of the rental payment is calculated at 9% interest rate. Find out whether it is advisable to rent the machine. (e^{−1 .08} = 0.3396) .

Solution:

Cost of the machine = 5, 00, 000 − 30, 000

=4, 70, 000

Hence it not advisable to rent the machine

It is better to buy the machine.

Inventory :

Given the inventory on hand I ( x ) and the unit holding cost (C₁), the total inventory carrying cost is C_{1 0}∫^T₀ I (x )dx, where T is the time period under consideration.

Example 3.22

A company receives a shipment of 200 cars every 30 days. From experience it is known that the inventory on hand is related to the number of days. Since the last shipment, I ( x)= 200 − 0.2x . Find the daily holding cost for maintaining inventory for 30 days if the daily holding cost is ₹3.5

Solution:

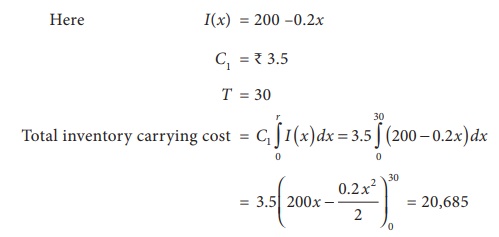
Amount of an Annuity

The amount of an annuity is the sum of all payments made plus all interest accumulated. Let an annuity consist of equal payments of Rs. p and let the interest rate of r percent annually be compounded continuously.

Amount of annuity after N payments A =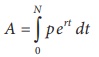 

Example 3.23

Mr. Arul invests ₹10,000 in ABC Bank each year, which pays an interest of 10% per annum compounded continuously for 5 years. How much amount will there be after 5 years. ( e^{0 .5} = 1.6487)

Solution:

p = 10000, r =  0.1, N = 5

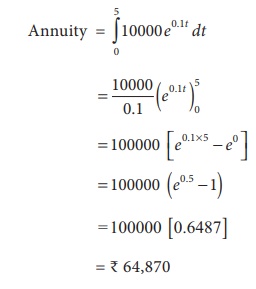
Consumption of a Natural Resource

Suppose that p(t) is the annual consumption of a natural resource in year t. If the consumption of the resource is growing exponentially at growth rate k, then the total consumption of the resource after T years is given by

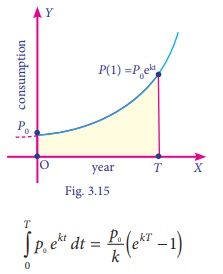
Where p₀ is the initial annual consumption at time t = 0.

Example 3.24

In year 2000 world gold production was 2547 metric tons and it was growing exponentially at the rate of 0.6% per year. If the growth continues at this rate, how many tons of gold will be produced from 2000 to 2013? [e^0.078 = 1.0811)

Solution:

Annual consumption at time t = 0 (In the year 2000) = p₀ = 2547  metric ton.

Total production of Gold from 2000 to 2013 =