Geometrical Interpretation of Definite Integral as Area under a curve

The area of the region bounded by the curves

Using integration we can evaluate the area bounded by the curves with coordinate axes. We can also calculate the area between two given curves.

Geometrical Interpretation of Definite Integral as Area under a curve:

Suppose we want to find out the area of the region which is bounded above by a curve y = f ( x) , below by the x − axis and the lines x = a and x = b .

Now from Fig 3.1 let the interval [a b] is divided into n subintervals [x_i-1, x_i] of equal length ∆x_i i.e x_i-x_i-1 = ∆_xi for any x_i’ ∈ [x_i-1,x_i], let f(x′_i) be the height  of n rectangles having x_i-x_i-1 = ∆x_i as its base. Then area A_i = ∆x_i f (x_i’). Now the total area A = 

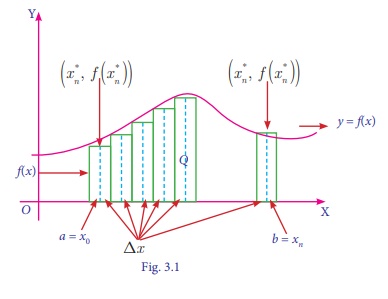
Now from the definition of definite integral, if f ( x) is a function defined on [ a , b] with a < b then the definite integral is

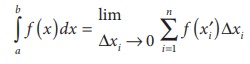
The area under the curve is exhausted by increasing the number of rectangular strips to ∞

Thus the geometrical interpretation of definite integral is the area under the curve between the given limits.

The area of the region bounded by the curve y=f(x), with x- axis and the ordinates at x = a and x = b given by

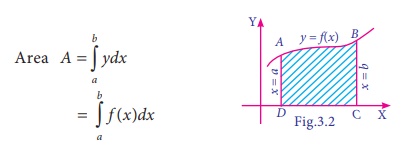
Note

(i) The area of the region bounded by the curve y = f (x) between the limits x = a , x = b and lies below x -axis, is

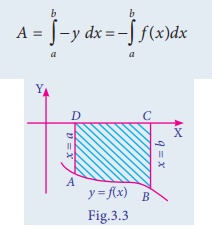
(ii)  The area of the region bounded by the curve x = f (y) between the limits y = c and y = d with y − axis and the area lies lies to the right of y- axis, is

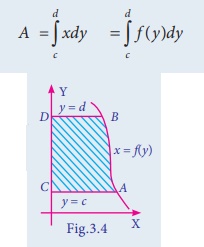
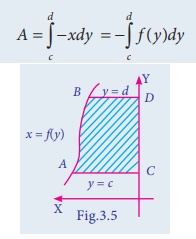
(iii) The area bounded by the curve x = f (y) between the limits y = c and y = d with y − axis and the area lies to the left of y- axis, is

Area between two curves

Let f(x) and g(x) be two continuous functions defined on x in the interval [a, b]. Also f (x) > g (x),a ≤ b

Then the area between these two curves from x = a to x = b , is

Example 3.1

Find the area bounded by y = 4x + 3 with x- axis between the lines x = 1 and x = 4

Solution:

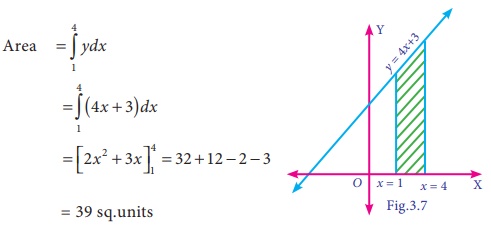
Example 3.2

Find the area of the region bounded by the line x − 2 y −12 = 0 , the y-axis and the lines y = 2, y = 5.

Solution:

x − 2 y −12 = 0

x = 2 y + 12

Required Area

Example 3.3

Find the area of the region bounded by the parabola y = 4 − x² , x − axis and the lines x = 0, x = 2

Solutions:

Example 3.4

Find the area bounded by y = x between the lines x = −1and x = 2 with x -axis.

Solutions:

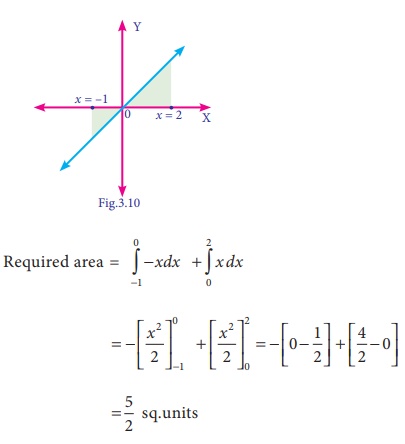
Example 3.5

Find the area of the parabola y ² = 8x bounded by its latus rectum.

Solution

y²=8x           (1)

Comparing this with the standard form y ² = 4ax ,

4a = 8

a = 2

Equation of latus rectum is x = 2

Since equation (1) is symmetrical about x- axis

Required Area = 2[Area in the first quadrant between the limits x = 0 and x = 2]

Example 3.6

Sketch the graph y = |x + 3| and evaluate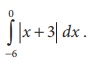 

Solution:

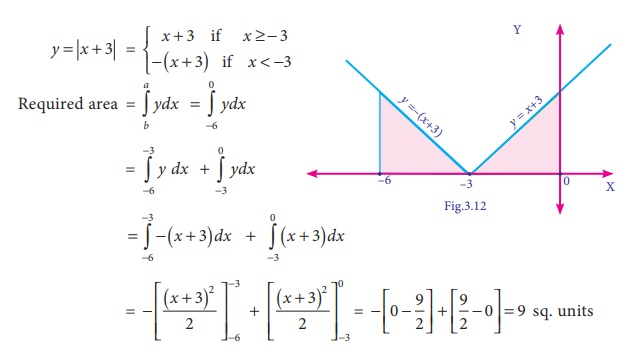
Example 3.7

Using integration find the area of the circle whose center is at the origin and the radius is a units.

Solution

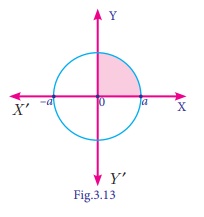
Equation of the required circle is x² + y² = a²               (1)

put y = 0, x² = a²

⇒ x = ± a

Since equation (1) is symmetrical about both the axes

The required area = 4 [Area in the first quadrant between the limit 0 and a.]

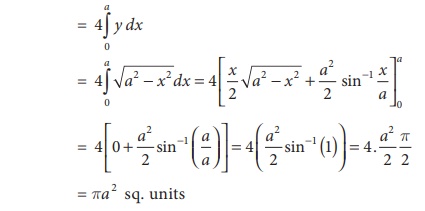
Example 3.8

Using integration find the area of the region bounded between the line x = 4 and the parabola y ² = 16x.

Solution:

The equation y ² = 16x represents a parabola (Open rightward)