Choose the best answer form the given alternatives

Choose the best answer form the given alternatives

1. Area bounded by the curve y = x ( 4 − x) between the limits 0 and 4 with x − axis is

 (a) 30/0 sq.units

(b) 31/2 sq.units

(c) 32/3 sq.units

(d) 15/2 sq.units

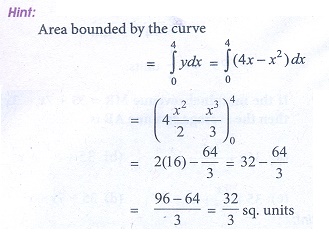
2. Area bounded by the curve y = e−2x between the limits 0 ≤ x ≤ ∞ is

(a) 1 sq.units

(b) 1/2 sq.unit

(c) 5 sq.units

(d) 2 sq.units

3. Area bounded by the curve y =1/x between the limits 1 and 2 is

(a) log2 sq.units x

(c) log3 sq.units

(d) log 4 sq.units

 (b) log5 sq.units

4. If the marginal revenue function of a firm is MR= e â€“x/10 , then revenue is

(a) −10e-x/10

(b) 1 − e-x/10

(c)10 (1 − e-x/10)

(d) e-x/10 + 10

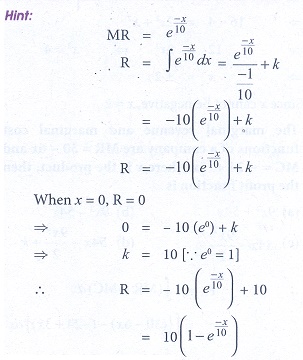
5. If MR and MC denotes the marginal revenue and marginal cost functions, then the profit functions is

(a) P = âˆ« ( MR âˆ’ MC ) dx + k

(b) P = âˆ« ( MR + MC ) dx + k

(c) P = âˆ« ( MR )( MC )dx + k

(d) P = âˆ« ( R â€“ C) dx + k

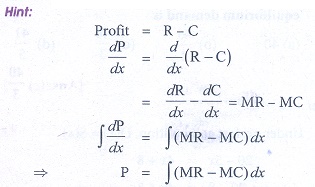
6. The demand and supply functions are given by D ( x)= 16 âˆ’ x2 and S ( x) = 2x2 + 4 are under perfect competition, then the equilibrium price x is

(a) 2

(b) 3

(c) 4

(d) 5

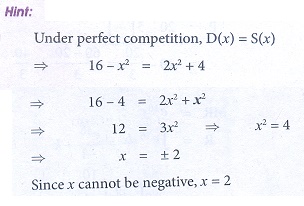
7. The marginal revenue and marginal cost functions of a company are MR = 30 − 6x and MC = −24 + 3x where x is the product, then the profit function is

 (a) 9x2 + 54x

(b) 9x2 âˆ’ 54x

(c) 54x − 9x2/2

(d) 54x – [9x2/2] + k

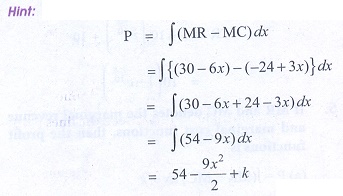
8. The given demand and supply function are given by D ( x) = 20 − 5x and S ( x) = 4x + 8 if they are under perfect competition then the equilibrium demand is

(a) 40

(b) 41/2

(c) 40/3

(d) 41/5

9. If the marginal revenue MR = 35 + 7x − 3x2 , then the average revenue AR is

(a) 35x + 7x2/2 − x3

(b) 35 + 7x/2 − x2

(c) 35 + 7x/2  + x2

(d) 35 + 7x + x2

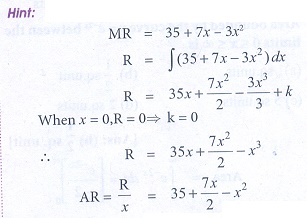
10. The profit of a function p(x) is maximum when

(a) MC − MR = 0

(b) MC=0

(c) MR=0

(d) MC+MR=0

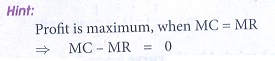
11. For the demand function p(x), the elasticity of demand with respect to price is unity then

(a) revenue is constant

(b) cost function is constant

(c) profit is constant

(d) none of these

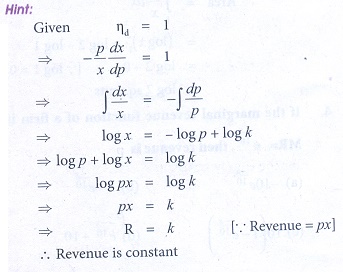
12. The demand function for the marginal function MR = 100 − 9x2 is

(a) 100 − 3x2

(b)100x − 3x2

(c)100x − 9x2

(d)100 + 9x2

13. When x0 = 5 and p0 = 3 the consumer’s surplus for the demand function pd = 28 − x2 is

(a) 250 units

(b) 250/3 units

(c) 251/2 units

(d) 251/3 units

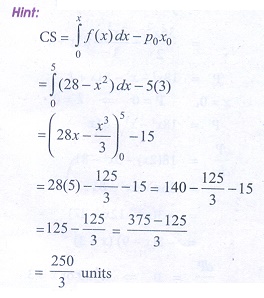
14. When x0 = 2 and P0 = 12 the producer’s surplus for the supply function Ps = 2x2 + 4 is

(a) 31/5 units

(b) 31/2 units

(c) 32/3 units

(d) 30/7 units

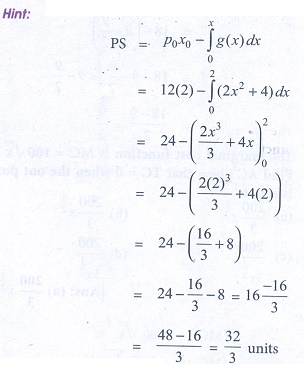
15. Area bounded by y = x between the lines y = 1, y = 2 with y = axis is

(a) 1/2 sq.units

(b) 5/2 sq.units

(c) 3/2 sq.units

(d) 1 sq.unit

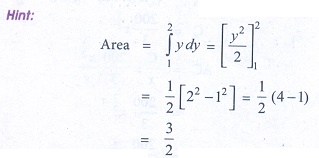
16. The producer’s surplus when the supply function for a commodity is P = 3 + x and x0 = 3 is

(a) 5/2

(b) 9/2

(c) 3/2

(d) 7/2

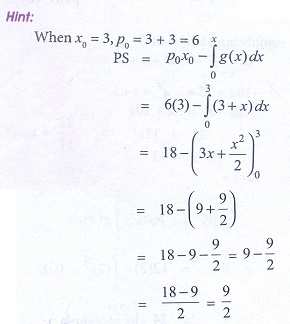
17. The marginal cost function is MC = 100√x. find AC given that TC =0 when the out put is zero is

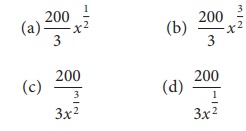
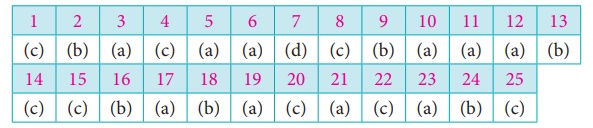
Ans: (a)

18. The demand and supply function of a commodity are P (x) = ( x − 5)2 and S (x) = x2 + x + 3 then the equilibrium quantity x0 is

(a) 5

(b) 2

(c) 3

(d) 19

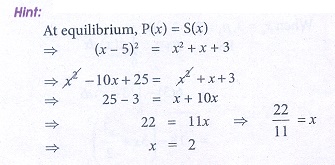
19. The demand and supply function of a commodity are D ( x)= 25 − 2x and S ( x) = [10 + x] /4 then the equilibrium price P0 is

(a) 5

(b) 2

(c) 3

(d) 10

20. If MR and MC denote the marginal revenue and marginal cost and MR − MC = 36x − 3x2 âˆ’ 81 , then the maximum profit at x is equal to

(a) 3

(b) 6

(c) 9

(d)5

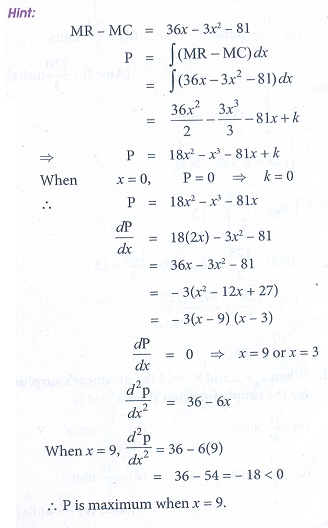
21. If the marginal revenue of a firm is constant, then the demand function is

(a) MR

(b) MC

(c) C ( x)

(d) AC

22. For a demand function p, if ∫ dp/p = k ∫ dx/x then k is equal to

(a) Î·d

(b) − Î·d

(c) -1/ Î·d

(d) 1/ Î·d

23. Area bounded by y = ex between the limits 0 to 1 is

(a) ( e −1) sq.units

(b) ( e + 1) sq.units

(c) (1 – 1/e) sq.units

(d) (1 + 1/e) sq.units

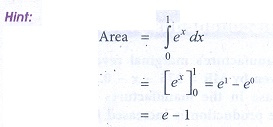
24. The area bounded by the parabola y2 = 4x bounded by its latus rectum is

(a) 16/3 sq.units

(b) 8/3 sq.units

(c) 72/3 sq.units

(d) 1/3 sq.units

25. Area bounded by y = |x| between the limits 0 and 2 is

 (a) 1sq.units

(b) 3 sq.units

(c) 2 sq.units

(d) 4 sq.units