Example Solved Problems with Answer, Solution, Formula - Integration: Cost functions from marginal cost functions | 12th Business Maths and Statistics : Chapter 3 : Integral Calculus - II
Chapter: 12th Business Maths and Statistics : Chapter 3 : Integral Calculus - II
Integration: Cost functions from marginal cost functions
Cost functions from marginal cost functions
If C is the cost of producing an output x, then
marginal cost function MC = dc/dx
Using integration, as the reverse process of differentiation, we
obtain,
Cost function C = Ōł½ ( MC ) dx + k
Where k is the constant of integration which is to be
evaluated,
Average cost function AC = C/X, x ŌēĀ
0
Example 3.9
The marginal cost function of manufacturing x shoes is 6 + 10x ŌłÆ 6x2 .
The cost producing a pair of shoes is Ōé╣12. Find the total and average cost
function.
Solution:
Given,
Marginal cost MC = 6 +
10x ŌłÆ 6x2
C = Ōł½ MC dx + k
= Ōł½( 6 +
10x ŌłÆ 6x2 ) dx + k
= 6x + 5x2 ŌłÆ 2x 3 + k (1)
When x= 2 , C = 12 (given)
12 = 12 +
20 ŌłÆ16 + k
k=-4
C = 6x + 5x2 ŌłÆ 2x3 ŌĆō 4
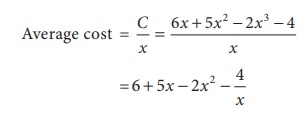
Example 3.10
A company has determined that the marginal cost function for a
product of a particular commodity is given by MC = 125 + 10x ŌłÆ x2/9 where
C rupees is the cost of 9 producing x units of the commodity. If the
fixed cost is Ōé╣250 what is the cost of producing 15 units.
Solution:
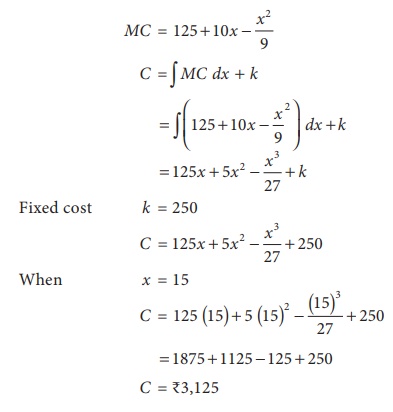
Example 3.11
The marginal cost function MC = 2 + 5ex (i)
Find C if C (0)=100 (ii) Find AC.
Solution:
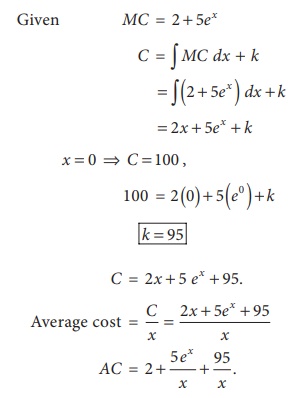
Rate of growth or sale
If the rate of growth or sale of a function is a known function of
t say f(t) where t is a time measure, then total
growth (or) sale of a product over a time period t is given by,
Total sale = 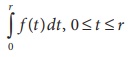
Example 3.12
The rate of new product is given by f (x) = 100 ŌłÆ 90 eŌłÆx where x is the
number of days the product is on the market. Find the total sale during the
first four days. (eŌĆō4=0.018)
Solution:
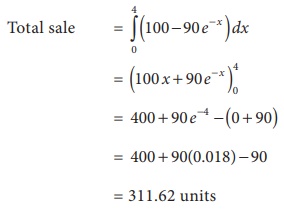
Example 3.13
A company produces 50,000 units per week with 200 workers. The
rate of change of productions with respect to the change in the number of
additional labour x is represented as 300 ŌłÆ 5x 2/3 . If 64 additional
labours are employed, find out the additional number of units, the company can
produce.
Solution:
Let p be the additional product produced for additional of x
labour,
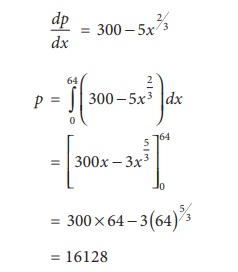
Ōł┤ The number of
additional units produced 16128
Total number of units produced by 264 workers
50,000 + 16,128 = 66128 units
Example 3.14
The rate of change of sales of a company after an advertisement
campaign is represented as, f (t ) = 3000e ŌłÆ0.3t where t
represents the number of months after the advertisement. Find out the total
cumulative sales after 4 months and the sales during the fifth month. Also find
out the total sales due to the advertisement campaign e ŌłÆ1 . 2 = 0.3012, eŌłÆ1.5 = 0.2231 .
Solution:

Example 3.15
The price of a machine is 6,40,000 if the rate of cost saving is
represented by the function f(t) = 20,000 t. Find out the
number of years required to recoup the cost of the function.
Solution:
Saving Cost S(t)
= Ōł½t0 20000t dt
= 10000 t2
To recoup the total price,
10000 t2 = 640000
t2 = 64
t = 8
When t = 8 years, one can recoup the price.
Related Topics