Example Solved Problems with Answer, Solution, Formula - Integration: Consumer’s surplus | 12th Business Maths and Statistics : Chapter 3 : Integral Calculus - II
Chapter: 12th Business Maths and Statistics : Chapter 3 : Integral Calculus - II
Integration: Consumer’s surplus
Consumer’s surplus:
This theory was developed by the great economist Marshal. The
demand function reveals the relationship between the quantities that the people
would buy at a given price. It can be expressed as p = f (x)
Let us assume that the demand of the product x = x0 when the price is p0. But
there can be
some consumer who is ready to pay q0 which is more than p
for the same quantity x0. Any consumer who
is ready to pay the price more than p0 gains from the fact
that the price is only p0. This gain is called the consumer’s
surplus.
It is represented in the following diagram
Mathematically the Consumer’s Surplus (CS) can be defined as
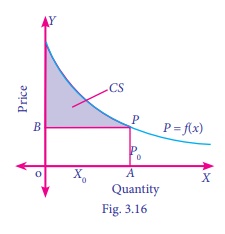
CS = (Area under the demand curve from x = 0 to x = x0 ) –
(Area of the rectangle OAPB)
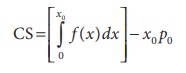
Example 3.27
The demand function of a commodity is y = 36 − x2 .
Find the consumer’s surplus for y0 = 11
Solution:
Related Topics