Exercise 3.2: Application of Integration in Economics and Commerce

Exercise 3.2

1. The cost of over haul of an engine is ₹10,000 The operating cost per hour is at the rate of 2x âˆ’ 240 where the engine has run x km. Find out the total cost if the engine run for 300 hours after overhaul.

2. Elasticity of a function Ey/ Ex is given by Ey/ Ex = −7x / (1 − 2x )( 2 + 3x ). Find the function when x = 2, y = 3/8 .

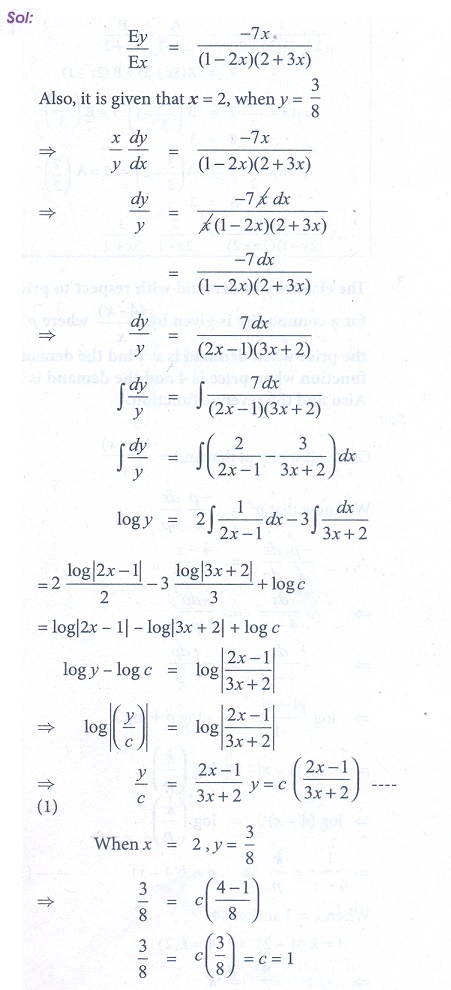
3. The elasticity of demand with respect to price for a commodity is given by ( 4 − x) / x ,  where p is the price when demand is x. Find the demand function when price is 4 and the demand is 2. Also find the revenue function.

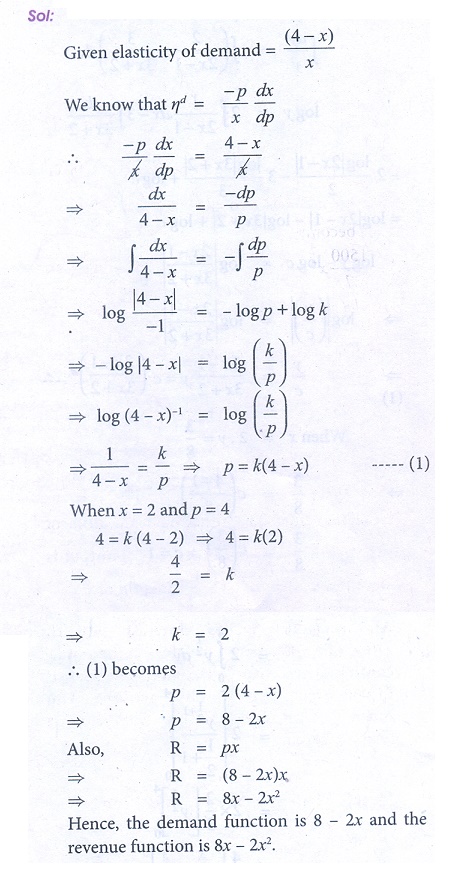
4. A company receives a shipment of 500 scooters every 30 days. From experience it is known that the inventory on hand is related to the number of days x. Since the shipment, I ( x) = 500 − 0.03x2 , the daily holding cost per scooter is ₹ 0.3. Determine the total cost for maintaining inventory for 30 days.

5. An account fetches interest at the rate of 5% per annum compounded continuously An individual deposits ₹1,000 each year in his account. How much will be in the account after 5 years. (e0.25 = 1.284) .

6. The marginal cost function of a product is given by dC/dx = 100 −10x + 0.1x2 where x is the output. Obtain the total and the average cost function of the firm under the assumption, that its fixed cost is ₹ 500.

7. The marginal cost function is MC = 300 x2/5 and fixed cost is zero. Find out the total cost and average cost functions.

8. If the marginal cost function of x units of output is a/ âˆš[ax + b] and if the cost of output is zero. Find the total cost as a function of x.

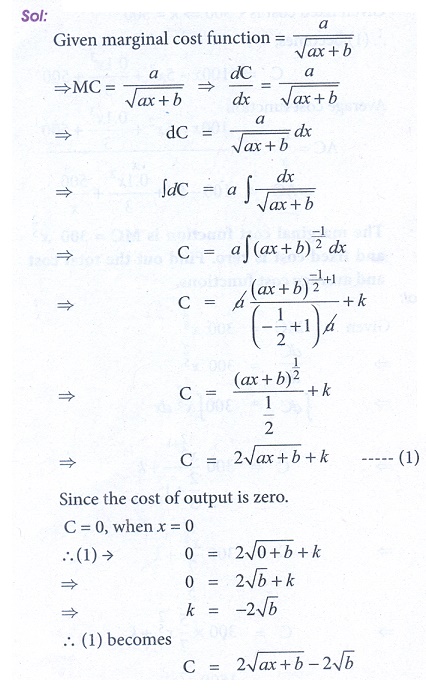
9. Determine the cost of producing 200 air conditioners if the marginal cost (is per unit) is C ′ ( x) = x2/200 + 4 .

10. The marginal revenue (in thousands of Rupees) functions for a particular commodity is 5 + 3 e−0 .03 x where x denotes the number of units sold. Determine the total revenue from the sale of 100 units. (Given e−3 = 0.05 approximately)

11. If the marginal revenue function for a commodity is MR = 9 − 4x2 . Find the demand function.

12. Given the marginal revenue function 4/( 2x + 3)2  âˆ’ 1 , show that the average revenue function is P = 4/[6x + 9] −1.

13.  A firm’s marginal revenue function is MR = 20e âˆ’x 10 (1− x/10). Find the corresponding demand function.

14. The marginal cost of production of a firm is given by C â€²(x) = 5 + 0.13x , the marginal revenue is given by R â€²(x) = 18 and the fixed cost is ₹ 120. Find the profit function.

15. If the marginal revenue function is R â€² ( x)= 1500 âˆ’ 4x âˆ’ 3x2 . Find the revenue function and average revenue function.

16. Find the revenue function and the demand function if the marginal revenue for x units is MR= 10 + 3x âˆ’ x2 .

17. The marginal cost function of a commodity is given by MC = 14000/√[7x + 4] and the fixed cost is ₹18,000.Find the total cost and average cost.

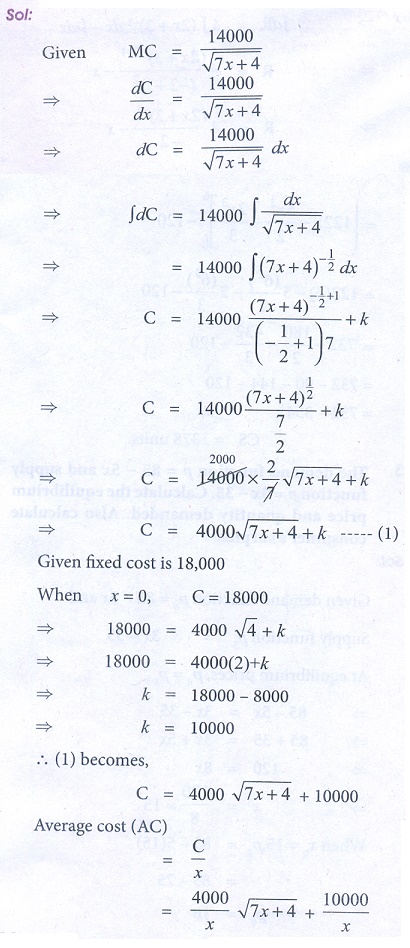
18. If the marginal cost (MC) of a production of the company is directly proportional to the number of units (x) produced, then find the total cost function, when the fixed cost is ₹ 5,000 and the cost of producing 50 units is ₹ 5,625.

19. If MR = 20 âˆ’ 5x + 3x2 , find total revenue function.

20. If MR = 14 âˆ’ 6x + 9x2 , find the demand function.