The General Heat Conduction Equation in Cartesian and Polar coordinates

The General Heat Conduction Equation in Cartesian coordinates and Polar coordinates

Any physical phenomenon is generally accompanied by a change in space and time of its physical properties. The heat transfer by conduction in solids can only take place when there is a variation of temperature, in both space and time. Let us consider a small volume of a solid element as shown in Fig. 1.2 The dimensions are x-, Y-, and Z- coordinates.

Fig 1.1 Elemental volume in Cartesian coordinates

First we consider heat conduction the X-direction. Let T denote the temperature at the point P (x, y, z) located at the geometric centre of the element. The temperature gradient at the left hand face (x - ~x12) and at the right hand face (x + x/2) , using the Taylor's series, can be written as:

¶T /  x¶|_L    =T/¶x   ¶²T /-x¶². x / 2¶+ higherD order terms.

¶T /  x¶|_R     =T/¶x   ¶²T /+x¶². x / 2¶ higherD order+ terms.

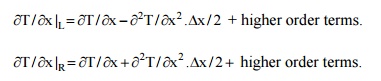
The net rate at which heat is conducted out of the element 10 X-direction assuming k as

constant and neglecting the higher order terms,

Similarly for Y- and Z-direction,

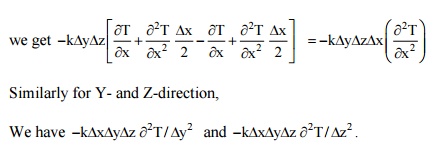
If there is heat generation within the element as Q, per unit volume and the internal energy of

the element changes with time, by making an energy balance, we write

 is called the thermal diffusivity and is seen to be a physical property of the material of which the solid is composed.

The Eq. (2.la) is the general heat conduction equation for an isotropic solid with a constant

Under steady state or stationary condition, the temperature of a body does not vary with time, i.e. ¶T / t¶ 0=.And, with no internal generation, the equation (2.1) reduces to

Del²T  =0

It should be noted that Fourier law can always be used to compute the rate of heat transfer by conduction from the knowledge of temperature distribution even for unsteady condition and with internal heat generation.