Unsteady Heat Conduction

UNSTEADY HEAT CONDUCTION :

Transient State Systems-Defined

The process of heat transfer by conduction where the temperature varies with time and with space coordinates, is called 'unsteady or transient'. All transient state systems may be broadly classified into two categories:

(a) Non-periodic Heat Flow System - the temperature at any point within the system changes as a non-linear function of time.

(b) Periodic Heat Flow System - the temperature within the system undergoes periodic changes which may be regular or irregular but definitely cyclic.

There are numerous problems where changes in conditions result in transient temperature distributions and they are quite significant. Such conditions are encountered in - manufacture of ceramics, bricks, glass and heat flow to boiler tubes, metal forming, heat treatment, etc.

 Biot and Fourier Modulus-Definition and Significance

Let us consider an initially heated long cylinder (L >> R) placed in a moving stream of fluid at

T_¥ <T_s , as shown In Fig. 3.1(a). The convective heat transfer coefficient at the surface is h, where,

Q = hA ( T_s -T_¥)

This energy must be conducted to the surface, and therefore,

Q = -kA(dT / dr) r = R            

or, h( Ts - Tm  ) = -k(dT/dr)r=R       = -k(Tc-Ts)/R      

where Tc is the temperature at the axis of the cylinder 

By rearranging,(Ts - Tc) / ( Ts - Tm  ) h/Rk         (3.1)

The term, hR/k, IS called the 'BlOT MODULUS'. It is a dimensionless number and is the ratio of internal heat flow resistance to external heat flow resistance and plays a fundamental role in transient conduction problems involving surface convection effects. I t provides a measure 0 f the temperature drop in the solid relative to the temperature difference between the surface and the fluid.

For Bi << 1, it is reasonable to assume a uniform temperature distribution across a solid at any time during a transient process.

Founer Modulus - It is also a dimensionless number and is defind as

Fo= at/L²             (3.2)

where L is the characteristic length of the body, a is the thermal diffusivity, and t is the time

The Fourier modulus measures the magnitude of the rate of conduction relative to the change in temperature, i.e., the unsteady effect. If Fo << 1, the change in temperature will be experienced by a region very close to the surface.

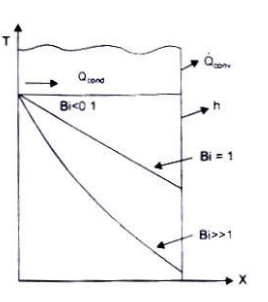
Fig. 1.7 Effect of Biot Modulus on steady state temperature distribution in a plane wall with surface convection.

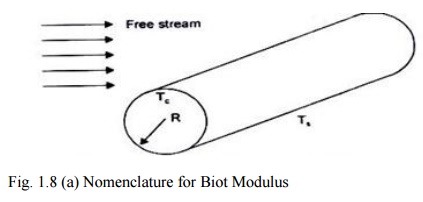
Fig. 1.8 (a) Nomenclature for Biot Modulus