Lumped Heat Analysis

LUMPED HEAT ANALYSIS:

Lumped Capacity System-Necessary Physical Assumptions

We know that a temperature gradient must exist in a material if heat energy is to be conducted into or out of the body. When Bi < 0.1, it is assumed that the internal thermal resistance of the body is very small in comparison with the external resistance and the transfer of heat energy is primarily controlled by the convective heat transfer at the surface. That is, the temperature within the body is approximately uniform. This idealised assumption is possible, if

(a) the physical size of the body is very small,

(b) the thermal conductivity of the material is very large, and

(c)   the convective heat transfer coefficient at the surface is very small and there is a large

temperature difference across the fluid layer at the interface.

An Expression for Evaluating the Temperature Variation in a Solid Using Lumped

Capacity Analysis

Let us consider a small metallic object which has been suddenly immersed in a fluid during a heat treatment operation. By applying the first law of

Heat flowing out of the body = Decrease in the internal thermal energy of

during a time dt the body during that time dt

or, hA_s( T -T_¥ )dt = - pCVdT

where A_s is the surface area of the body, V is the volume of the body and C is the specific heat capacity.

or, (hA/ rCV)dt = - dT /( T -T_¥)

with the initial condition being: at t = 0, T = T_s

The solution is : ( T -T_¥)/( T_s -T_¥) = exp(-hA / rCV)t

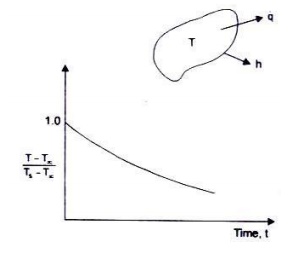
Fig. depicts the cooling of a body (temperature distribution time) using lumped thermal capacity system. The temperature history is seen to be an exponential decay.

We can express

Bi × Fo = (hL/k)×( at/L²) = (hL/k)(k/ rC)(t/L²) = (hA/ rCV)t,

where V / A is the characteristic length L.

And, the solution describing the temperature variation of the object with respect to time is given

( T -T_¥)/( T_s -T_¥) = exp(-Bi· Fo)