One Dimensional Steady State Equation Plane Wall

ONE DIMENSIONAL STEADY STATE EQUATION PLANE WALL :

The term 'one-dimensional' is applied to heat conduction problem when:

(i)             Only one space coordinate is required to describe the temperature distribution within a heat conducting body;

(ii)           Edge effects are neglected;

(iii)        The flow of heat energy takes place along the coordinate measured normal to the surface.

A plane wall is considered to be made out of a constant thermal conductivity material and extends to infinity in the Y- and Z-direction. The wall is assumed to be homogeneous and isotropic, heat flow is one-dimensional, under steady state conditions and losing negligible energy through the edges of the wall under the above mentioned assumptions the Eq. (2.2) reduces to

d²T / dx² = 0; the boundary conditions are: at    x = 0, T = T₁

Integrating the above equation,              x = L, T = T₂

T = C₁x + C₂, where C₁ and C₂ are two constants.

Substituting the boundary conditions, we get C₂  = T₁  and C₁  = (T₂  –T₁)/L The temperature

distribution in the plane wall is given by 

T = T1 –(T1 –T2) x/L  (2.3)

which is linear and is independent of the material.      

small for the same heat flow rate,"

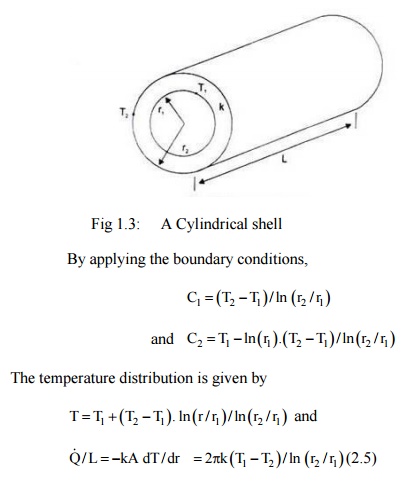
A Cylindrical Shell-Expression for Temperature Distribution

In the cylindrical system, when the temperature is a function of radial distance only and is independent of azimuth angle or axial distance, the differential equation (2.2) would be, (Fig. 1.4)

d²T /dr² +(1/r) dT/dr = 0

with boundary conditions: at r = r_l, T = T₁ and at r = r₂, T = T₂.

The differential equation can be written as:

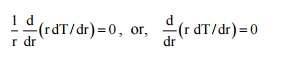
upon integration, T = C₁ ln (r) + C₂, where C₁ and C₂ are the arbitrary constants.

From Eq (2.5) It can be seen that the temperature varies 10gantJunically through the cylinder wall In contrast with the linear variation in the plane wall .

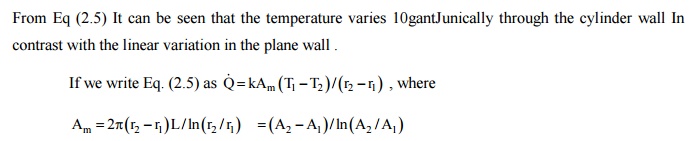
where  A₂  and  A₁  are  the  outside  and  inside  surface  areas  respectively.  The  term  A_m  is  called

‘Logarithmic  Mean   Area'   and   the   expression   for heat low through a cylidercal wall has the same 

form as that for a plane wall.