Steady State Solution of DC Circuits and Problems based on ohm’s law

Steady State Solution of DC Circuits:

Resistance in series connection:

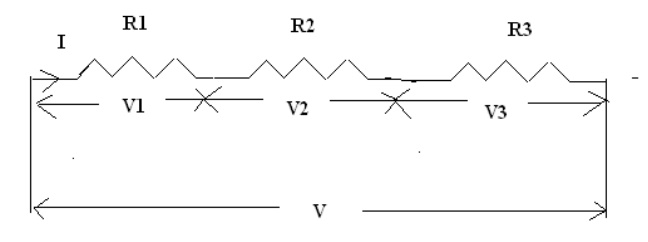
The resistors R₁, R₂, R₃ are connected in series across the supply voltage “V”. The total current flowing through the circuit is denoted as “I”. The voltage across the resistor R₁, R₂ and R₃ is V₁, V₂, and V₃ respectively.

V₁ = I*R₁ (as per ohms law)

V₂= I*R₂

V₃ = I*R₃

V = V₁+V₂+V₃

= IR₁+IR₂+IR₃

= (R₁+R₂+R₃) I IR = (R₁+R₂+R₃) I

R = R₁+R₂+R₃

Resistance in parallel connection:

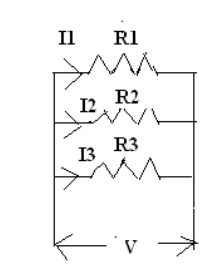
The resistors R₁, R₂, R₃ are connected in parallel across the supply voltage “V”. The total current flowing through the circuit is denoted as “I”. The current flowing through the resistor

R₁, R₂ and R₃ is I₁, I₂, and I₃ respectively.

I = V / R (as per ohms law)

I ₁ = V₁ / R₁

I₂ = V₂ / R₂

I₃ = V₃ / R₃

V₁ = V₂ = V₃ = V

From the above diagram

I  = I₁+I₂+I₃

= V₁ / R₁ + V₂ / R₂ + V₃ / R₃

= V / R₁+ V/R₂ +V/R₃

I  = V (1/R₁ +1/R₂ +1/R₃)

V / R = V (1/R₁ +1/R₂ +1/R₃)

1/R = 1/R₁ +1/R₂ +1/R₃

Problems based on ohm’s law

Problem 1:

A current of 0.5 A is flowing through the resistance of 10Ω.Find the potential difference between its ends.

Given data:

Current  I= 0.5A.

Resistance R=1Ω

T o f i n d

Potential difference V = ?

Formula used:

V = IR

Solution:

V = 0.5 × 10 = 5V.

Result :

The potential difference between its ends = 5 V

Problem :2

A supply voltage of 220V is applied to a 100 Ω resistor. Find the current flowing through

it.

Given data

Voltage V =  220V

Resistance R   = 100Ω

To find:

Current I = ?

Formula used:

Current I = V / R

Solution:

Current I = 220/100

= 2.2 A

Result:

The current flowing through the resistor = 2.2 A

Problem : 3

Calculate the resistance of the conductor if a current of 2A flows through it when the potential difference across its ends is 6V.

Given data

Current I = 2A

Voltage V = 6V

To find:

Resistance R = ?

Formula used:

Resistance R = V / I

Solution:

Resistance R = 6 / 2

= 3 Ω

Result:

The value of resistance R = 3Ω

Problem: 4

Calculate the current and resistance of a 100 W,  200V electric bulb.

Given data:

Power P = 100W

Voltage V = 200V

To find:

Current I =?

Resistance R =?

Formula used:

Power P = V *I

Current I = P / V

Resistance R = V / I

Solution:

Current I = P / V

= 100 / 200

= 0.5 A Resistance R = V / I

= 200 / 0.2

= 400 Ω

Result:

The value of the current I = 0.5 A

The value of the Resistance R = 400 Ω

Problem: 5

A circuit is made of 0.4 Ω wire, a 150Ω bulb and a 120Ω rheostat connected in series. Determine the total resistance of the circuit.

Given data:

Resistance of the wire = 0.4Ω

Resistance of bulb       = 1 5 0 Ω

Resistance of rheostat =        120Ω

To find:

The total resistance of the circuit R _T =?

Formula used:

The total resistance of the circuit R _T = R₁+R₂+R₃

_Solution:

_{Total resistance ,R               =  0.4 + 150 +120}

            _{= 270.4Ω}

_Result:

The total resistance of the circuit R _T = 270.4 Ω

Problem 6:

Three resistances of values 2Ω, 3Ω and 5Ω are connected in series across 20 V, D.C  supply

.Calculate (a) equivalent resistance of the circuit (b) the total current of the circuit (c) the voltage drop across each resistor and (d) the power dissipated in each resistor.

Given data:

R₁ = 2Ω

R₂ = 3Ω

R₃ = 5Ω

V = 20V

To find:

R _T =?

I _T =?

V₁, V₂, V₃ =?

P₁, P₂, P₃ =?

Formula used:

R_T = R₁+R₂+R₃ (series connection)

I_T = V_T / R_T

V₁ = R₁*I₁

V₂= R₂*I₂

V₃ = R₃*I₃

P₁=V₁*I₁

P₂=V₂*I₂

P₃=V₃*I₃

Solution:

R_T = R₁+R₂+R₃ = 2+3+5

R_T = 10Ω

I_T = V_T / R_T = 20 / 10

I_T = 2 A

In series connection I₁ = I₂ = I₃ = I_T = 2A

V₁ = I₁*R₁ = 2*2

V₁ = 4 V

V₂ = I₂*R₂ = 2*3

V₂ = 6 V

V₃ = I₃*R₃ = 5*2

V₃ = 10V

P₁ = V₁*I₁

= 4*2

P₁ = 8W

P₂ = V₂*I₂

= 6*2

P₂ = 12W

P₃ = V₃*I₃ = 10*2

P₃ = 20W

Result:

(a). Equivalent resistance of the circuit R_T = 10Ω

(b). The total current of the  circuit I_T = 2A

(c). Voltage drop across each resistor V₁ = 4 V, V₂ = 6 V, V₃ = 10V

(d). The power dissipated in each resistor P₁ = 8W, P₂ = 12W, P₃ = 20W